Menu Close

Question-38373

Tinku Tara 0 Comments
Pin




Question Number 38373 by tanmay.chaudhury50@gmail.com last updated on 24/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
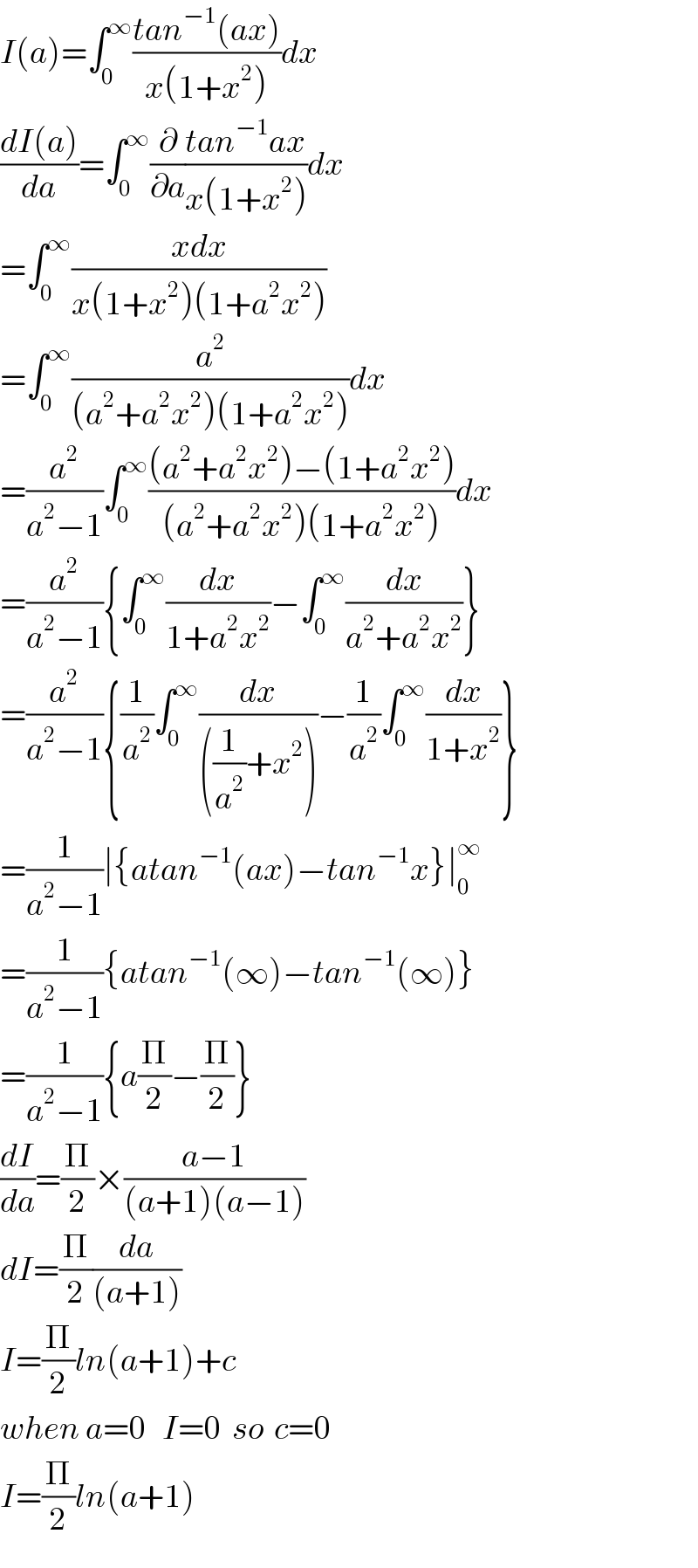
I(a)=∫_0 ^∞ ((tan^(−1) (ax))/(x(1+x^2 )))dx ((dI(a))/da)=∫_0 ^∞ (∂/∂a)((tan^(−1) ax)/(x(1+x^2 )))dx =∫_0 ^∞ ((xdx)/(x(1+x^2 )(1+a^2 x^2 ))) =∫_0 ^∞ (a^2 /((a^2 +a^2 x^2 )(1+a^2 x^2 )))dx =(a^2 /(a^2 −1))∫_0 ^∞ (((a^2 +a^2 x^2 )−(1+a^2 x^2 ))/((a^2 +a^2 x^2 )(1+a^2 x^2 )))dx =(a^2 /(a^2 −1)){∫_0 ^∞ (dx/(1+a^2 x^2 ))−∫_0 ^∞ (dx/(a^2 +a^2 x^2 ))} =(a^2 /(a^2 −1)){(1/a^2 )∫_0 ^∞ (dx/(((1/a^2 )+x^2 )))−(1/a^2 )∫_0 ^∞ (dx/(1+x^2 ))} =(1/(a^2 −1))∣{atan^(−1) (ax)−tan^(−1) x}∣_0 ^∞ =(1/(a^2 −1)){atan^(−1) (∞)−tan^(−1) (∞)} =(1/(a^2 −1)){a(Π/2)−(Π/2)} (dI/da)=(Π/2)×((a−1)/((a+1)(a−1))) dI=(Π/2)(da/((a+1))) I=(Π/2)ln(a+1)+c when a=0 I=0 so c=0 I=(Π/2)ln(a+1)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{tan}^{−\mathrm{1}} \left({ax}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$\frac{{dI}\left({a}\right)}{{da}}=\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial{a}}\frac{{tan}^{−\mathrm{1}} {ax}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{xdx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{a}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \frac{\left({a}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)−\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{1}}\left\{\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{1}}\left\{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+{x}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\mid\left\{{atan}^{−\mathrm{1}} \left({ax}\right)−{tan}^{−\mathrm{1}} {x}\right\}\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left\{{atan}^{−\mathrm{1}} \left(\infty\right)−{tan}^{−\mathrm{1}} \left(\infty\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left\{{a}\frac{\Pi}{\mathrm{2}}−\frac{\Pi}{\mathrm{2}}\right\} \\ $$$$\frac{{dI}}{{da}}=\frac{\Pi}{\mathrm{2}}×\frac{{a}−\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right)} \\ $$$${dI}=\frac{\Pi}{\mathrm{2}}\frac{{da}}{\left({a}+\mathrm{1}\right)} \\ $$$${I}=\frac{\Pi}{\mathrm{2}}{ln}\left({a}+\mathrm{1}\right)+{c} \\ $$$${when}\:{a}=\mathrm{0}\:\:\:{I}=\mathrm{0}\:\:{so}\:\:{c}=\mathrm{0} \\ $$$${I}=\frac{\Pi}{\mathrm{2}}{ln}\left({a}+\mathrm{1}\right) \\ $$
Commented by math khazana by abdo last updated on 25/Jun/18
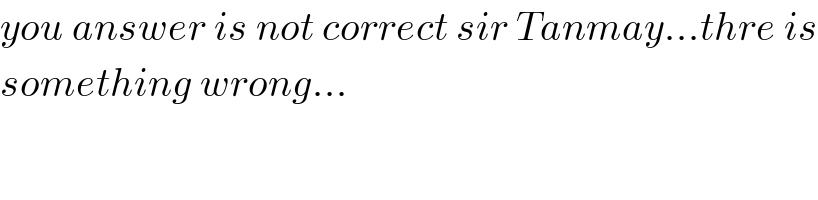
you answer is not correct sir Tanmay...thre is something wrong...
$${you}\:{answer}\:{is}\:{not}\:{correct}\:{sir}\:{Tanmay}…{thre}\:{is} \\ $$$${something}\:{wrong}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
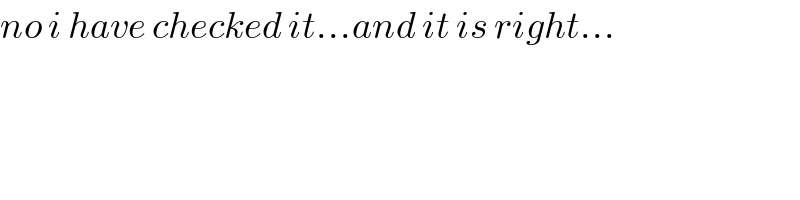
no i have checked it...and it is right...
$${no}\:{i}\:{have}\:{checked}\:{it}…{and}\:{it}\:{is}\:{right}… \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
Commented by prof Abdo imad last updated on 25/Jun/18
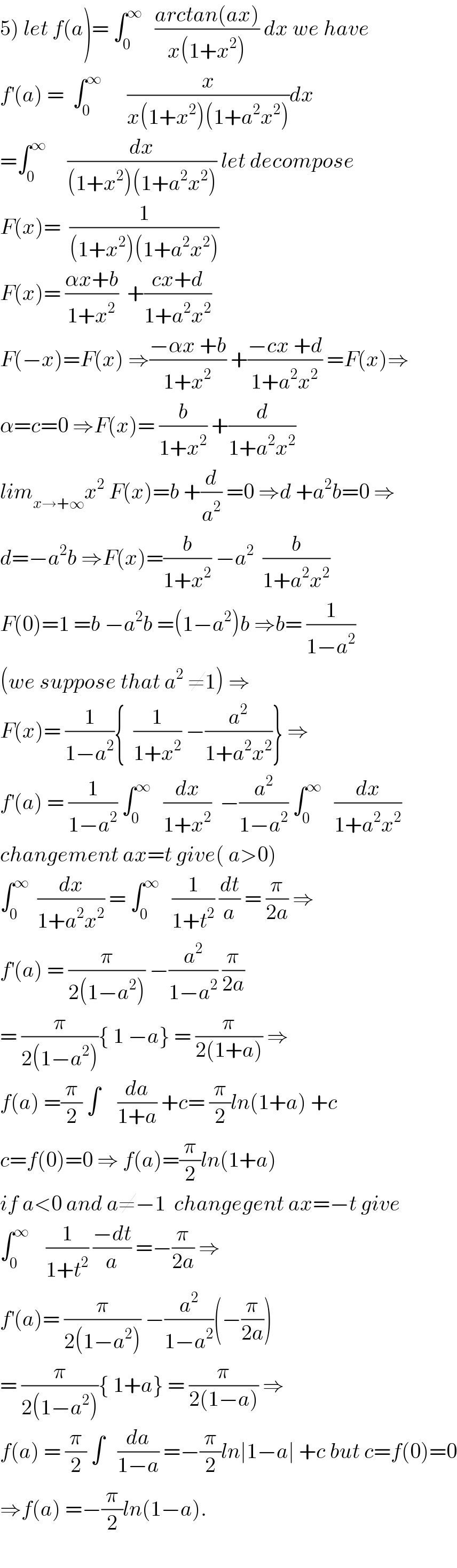
5) let f(a)= ∫_0 ^∞ ((arctan(ax))/(x(1+x^2 ))) dx we have f^′ (a) = ∫_0 ^∞ (x/(x(1+x^2 )(1+a^2 x^2 )))dx =∫_0 ^∞ (dx/((1+x^2 )(1+a^2 x^2 ))) let decompose F(x)= (1/((1+x^2 )(1+a^2 x^2 ))) F(x)= ((αx+b)/(1+x^2 )) +((cx+d)/(1+a^2 x^2 )) F(−x)=F(x) ⇒((−αx +b)/(1+x^2 )) +((−cx +d)/(1+a^2 x^2 )) =F(x)⇒ α=c=0 ⇒F(x)= (b/(1+x^2 )) +(d/(1+a^2 x^2 )) lim_(x→+∞) x^2 F(x)=b +(d/a^2 ) =0 ⇒d +a^2 b=0 ⇒ d=−a^2 b ⇒F(x)=(b/(1+x^2 )) −a^2 (b/(1+a^2 x^2 )) F(0)=1 =b −a^2 b =(1−a^2 )b ⇒b= (1/(1−a^2 )) (we suppose that a^2 ≠1) ⇒ F(x)= (1/(1−a^2 )){ (1/(1+x^2 )) −(a^2 /(1+a^2 x^2 ))} ⇒ f^′ (a) = (1/(1−a^2 )) ∫_0 ^∞ (dx/(1+x^2 )) −(a^2 /(1−a^2 )) ∫_0 ^∞ (dx/(1+a^2 x^2 )) changement ax=t give( a>0) ∫_0 ^∞ (dx/(1+a^2 x^2 )) = ∫_0 ^∞ (1/(1+t^2 )) (dt/a) = (π/(2a)) ⇒ f^′ (a) = (π/(2(1−a^2 ))) −(a^2 /(1−a^2 )) (π/(2a)) = (π/(2(1−a^2 ))){ 1 −a} = (π/(2(1+a))) ⇒ f(a) =(π/2) ∫ (da/(1+a)) +c= (π/2)ln(1+a) +c c=f(0)=0 ⇒ f(a)=(π/2)ln(1+a) if a<0 and a≠−1 changegent ax=−t give ∫_0 ^∞ (1/(1+t^2 )) ((−dt)/a) =−(π/(2a)) ⇒ f^′ (a)= (π/(2(1−a^2 ))) −(a^2 /(1−a^2 ))(−(π/(2a))) = (π/(2(1−a^2 ))){ 1+a} = (π/(2(1−a))) ⇒ f(a) = (π/2) ∫ (da/(1−a)) =−(π/2)ln∣1−a∣ +c but c=f(0)=0 ⇒f(a) =−(π/2)ln(1−a).
$$\left.\mathrm{5}\right)\:{let}\:{f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({ax}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}\:{we}\:{have} \\ $$$${f}^{'} \left({a}\right)\:=\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{x}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)} \\ $$$${F}\left({x}\right)=\:\frac{\alpha{x}+{b}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:+\frac{{cx}+{d}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${F}\left(−{x}\right)={F}\left({x}\right)\:\Rightarrow\frac{−\alpha{x}\:+{b}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+\frac{−{cx}\:+{d}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }\:={F}\left({x}\right)\Rightarrow \\ $$$$\alpha={c}=\mathrm{0}\:\Rightarrow{F}\left({x}\right)=\:\frac{{b}}{\mathrm{1}+{x}^{\mathrm{2}} }\:+\frac{{d}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow+\infty} {x}^{\mathrm{2}} \:{F}\left({x}\right)={b}\:+\frac{{d}}{{a}^{\mathrm{2}} }\:=\mathrm{0}\:\Rightarrow{d}\:+{a}^{\mathrm{2}} {b}=\mathrm{0}\:\Rightarrow \\ $$$${d}=−{a}^{\mathrm{2}} {b}\:\Rightarrow{F}\left({x}\right)=\frac{{b}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−{a}^{\mathrm{2}} \:\:\frac{{b}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:={b}\:−{a}^{\mathrm{2}} {b}\:=\left(\mathrm{1}−{a}^{\mathrm{2}} \right){b}\:\Rightarrow{b}=\:\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} } \\ $$$$\left({we}\:{suppose}\:{that}\:{a}^{\mathrm{2}} \:\neq\mathrm{1}\right)\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\left\{\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:−\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${changement}\:{ax}={t}\:{give}\left(\:{a}>\mathrm{0}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{{dt}}{{a}}\:=\:\frac{\pi}{\mathrm{2}{a}}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)}\:−\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }\:\frac{\pi}{\mathrm{2}{a}} \\ $$$$=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)}\left\{\:\mathrm{1}\:−{a}\right\}\:=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{a}\right)}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}\:\int\:\:\:\:\frac{{da}}{\mathrm{1}+{a}}\:+{c}=\:\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{1}+{a}\right)\:+{c} \\ $$$${c}={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:{f}\left({a}\right)=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{1}+{a}\right) \\ $$$${if}\:{a}<\mathrm{0}\:{and}\:{a}\neq−\mathrm{1}\:\:{changegent}\:{ax}=−{t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\frac{−{dt}}{{a}}\:=−\frac{\pi}{\mathrm{2}{a}}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)}\:−\frac{{a}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }\left(−\frac{\pi}{\mathrm{2}{a}}\right) \\ $$$$=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)}\left\{\:\mathrm{1}+{a}\right\}\:=\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{a}\right)}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\:\frac{\pi}{\mathrm{2}}\:\int\:\:\:\frac{{da}}{\mathrm{1}−{a}}\:=−\frac{\pi}{\mathrm{2}}{ln}\mid\mathrm{1}−{a}\mid\:+{c}\:{but}\:{c}={f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left({a}\right)\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{1}−{a}\right). \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *