Menu Close

Question-38533

Tinku Tara 0 Comments
Pin




Question Number 38533 by behi83417@gmail.com last updated on 26/Jun/18
Commented by math khazana by abdo last updated on 03/Aug/18
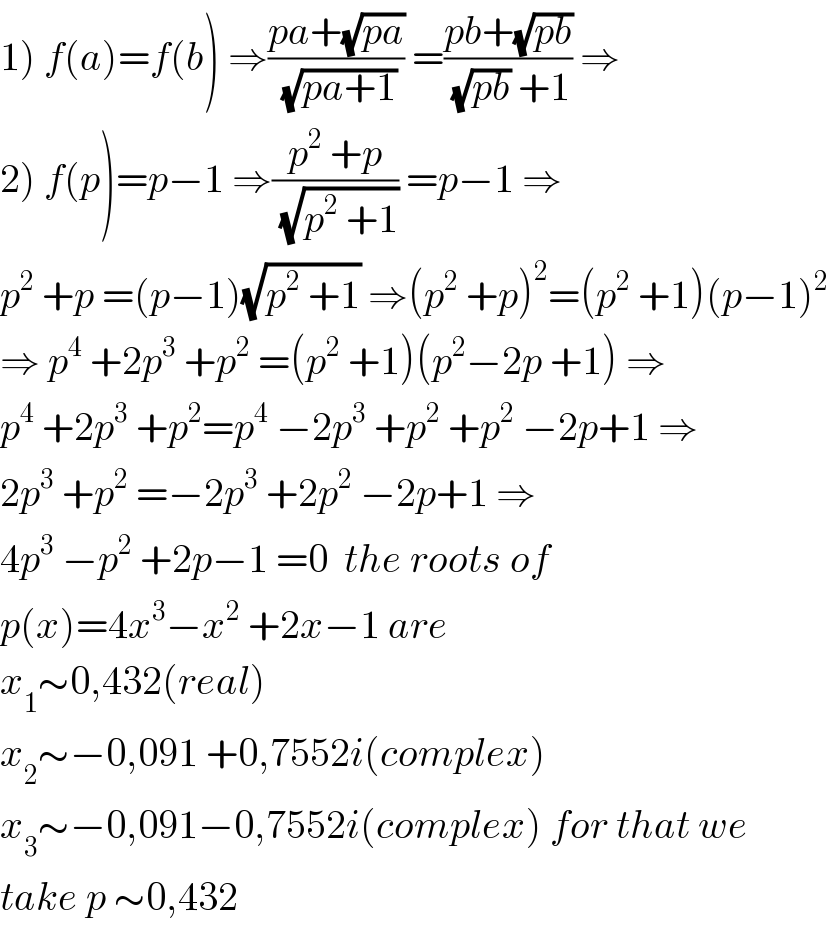
1) f(a)=f(b) ⇒((pa+(√(pa)))/( (√(pa+1)))) =((pb+(√(pb)))/( (√(pb)) +1)) ⇒ 2) f(p)=p−1 ⇒((p^2 +p)/( (√(p^2 +1)))) =p−1 ⇒ p^2 +p =(p−1)(√(p^2 +1)) ⇒(p^2 +p)^2 =(p^2 +1)(p−1)^2 ⇒ p^4 +2p^3 +p^2 =(p^2 +1)(p^2 −2p +1) ⇒ p^4 +2p^3 +p^2 =p^4 −2p^3 +p^2 +p^2 −2p+1 ⇒ 2p^3 +p^2 =−2p^3 +2p^2 −2p+1 ⇒ 4p^3 −p^2 +2p−1 =0 the roots of p(x)=4x^3 −x^2 +2x−1 are x_1 ∼0,432(real) x_2 ∼−0,091 +0,7552i(complex) x_3 ∼−0,091−0,7552i(complex) for that we take p ∼0,432
$$\left.\mathrm{1}\right)\:{f}\left({a}\right)={f}\left({b}\right)\:\Rightarrow\frac{{pa}+\sqrt{{pa}}}{\:\sqrt{{pa}+\mathrm{1}}}\:=\frac{{pb}+\sqrt{{pb}}}{\:\sqrt{{pb}}\:+\mathrm{1}}\:\Rightarrow \\ $$$$\left.\mathrm{2}\right)\:{f}\left({p}\right)={p}−\mathrm{1}\:\Rightarrow\frac{{p}^{\mathrm{2}} \:+{p}}{\:\sqrt{{p}^{\mathrm{2}} \:+\mathrm{1}}}\:={p}−\mathrm{1}\:\Rightarrow \\ $$$${p}^{\mathrm{2}} \:+{p}\:=\left({p}−\mathrm{1}\right)\sqrt{{p}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\left({p}^{\mathrm{2}} \:+{p}\right)^{\mathrm{2}} =\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({p}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{p}^{\mathrm{4}} \:+\mathrm{2}{p}^{\mathrm{3}} \:+{p}^{\mathrm{2}} \:=\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({p}^{\mathrm{2}} −\mathrm{2}{p}\:+\mathrm{1}\right)\:\Rightarrow \\ $$$${p}^{\mathrm{4}} \:+\mathrm{2}{p}^{\mathrm{3}} \:+{p}^{\mathrm{2}} ={p}^{\mathrm{4}} \:−\mathrm{2}{p}^{\mathrm{3}} \:+{p}^{\mathrm{2}} \:+{p}^{\mathrm{2}} \:−\mathrm{2}{p}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{2}{p}^{\mathrm{3}} \:+{p}^{\mathrm{2}} \:=−\mathrm{2}{p}^{\mathrm{3}} \:+\mathrm{2}{p}^{\mathrm{2}} \:−\mathrm{2}{p}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{4}{p}^{\mathrm{3}} \:−{p}^{\mathrm{2}} \:+\mathrm{2}{p}−\mathrm{1}\:=\mathrm{0}\:\:{the}\:{roots}\:{of} \\ $$$${p}\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}\:{are} \\ $$$${x}_{\mathrm{1}} \sim\mathrm{0},\mathrm{432}\left({real}\right) \\ $$$${x}_{\mathrm{2}} \sim−\mathrm{0},\mathrm{091}\:+\mathrm{0},\mathrm{7552}{i}\left({complex}\right) \\ $$$${x}_{\mathrm{3}} \sim−\mathrm{0},\mathrm{091}−\mathrm{0},\mathrm{7552}{i}\left({complex}\right)\:{for}\:{that}\:{we} \\ $$$${take}\:{p}\:\sim\mathrm{0},\mathrm{432} \\ $$
Commented by math khazana by abdo last updated on 03/Aug/18
p=0,432 is not solution because p−1<0?and ((p^2 +p)/( (√(p^2 +1)))) >0 so the equation is impossible.
$${p}=\mathrm{0},\mathrm{432}\:{is}\:{not}\:{solution}\:\:{because}\:{p}−\mathrm{1}<\mathrm{0}?{and} \\ $$$$\frac{{p}^{\mathrm{2}} \:+{p}}{\:\sqrt{{p}^{\mathrm{2}} \:+\mathrm{1}}}\:>\mathrm{0}\:\:{so}\:{the}\:{equation}\:{is}\:{impossible}. \\ $$
Answered by behi83417@gmail.com last updated on 27/Jun/18
((p^2 +p)/( (√(p^2 +1))))=p−1⇒p(p+1)=(p−1)(√(p^2 +1)) ⇒p^2 (p^2 +2p+1)=(p^2 −2p+1)(p^2 +1) ⇒4p^3 −p^2 +2p−1=0⇒p=0.43
$$\frac{{p}^{\mathrm{2}} +{p}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}={p}−\mathrm{1}\Rightarrow{p}\left({p}+\mathrm{1}\right)=\left({p}−\mathrm{1}\right)\sqrt{{p}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{p}^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{2}{p}+\mathrm{1}\right)=\left({p}^{\mathrm{2}} −\mathrm{2}{p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{4}\boldsymbol{{p}}^{\mathrm{3}} −\boldsymbol{{p}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{p}}−\mathrm{1}=\mathrm{0}\Rightarrow\boldsymbol{{p}}=\mathrm{0}.\mathrm{43}\: \\ $$
Commented by MrW3 last updated on 27/Jun/18
((0.43^2 +0.43)/( (√(0.43^2 +1))))=0.57 ! 0.43−1=−0.57 ! i.e. p=0.43 is not a solution of the original equation! I think you know where the error lies, see following example: (√(x+1))=−2 (it has no solution), but ((√(x+1)))^2 =(−2)^2 ⇒x+1=4⇒x=3
$$\frac{\mathrm{0}.\mathrm{43}^{\mathrm{2}} +\mathrm{0}.\mathrm{43}}{\:\sqrt{\mathrm{0}.\mathrm{43}^{\mathrm{2}} +\mathrm{1}}}=\mathrm{0}.\mathrm{57}\:! \\ $$$$\mathrm{0}.\mathrm{43}−\mathrm{1}=−\mathrm{0}.\mathrm{57}\:! \\ $$$${i}.{e}.\:{p}=\mathrm{0}.\mathrm{43}\:{is}\:{not}\:{a}\:{solution}\:{of}\:{the} \\ $$$${original}\:{equation}! \\ $$$${I}\:{think}\:{you}\:{know}\:{where}\:{the}\:{error} \\ $$$${lies},\:{see}\:{following}\:{example}: \\ $$$$\sqrt{{x}+\mathrm{1}}=−\mathrm{2}\:\left({it}\:{has}\:{no}\:{solution}\right),\:{but} \\ $$$$\left(\sqrt{{x}+\mathrm{1}}\right)^{\mathrm{2}} =\left(−\mathrm{2}\right)^{\mathrm{2}} \Rightarrow{x}+\mathrm{1}=\mathrm{4}\Rightarrow{x}=\mathrm{3} \\ $$
Commented by behi83417@gmail.com last updated on 27/Jun/18
thank you so much dear master. you are right. it should be :p>1.
$${thank}\:\:{you}\:{so}\:{much}\:{dear}\:{master}. \\ $$$${you}\:{are}\:{right}.\:{it}\:{should}\:{be}\::{p}>\mathrm{1}. \\ $$
Answered by MrW3 last updated on 27/Jun/18
f′(x)=(px+(√(px)))(−(p/(2(px+1)(√(px+1)))))+(1/( (√(px+1))))(p+(p/(2(√(px))))) f′(x)=(p/2)[−((√(px))/(px+1))+(1/( (√(px))))] f′(x)=(p/(2(px+1)(√(px)))) f′(x) >0 if p>0 f′(x) <0 if p<0 i.e. f(x) is always increasing or always decreasing. i.e. if f(a)=f(b)⇒a=b⇒(a/b)=1 f(p)=((p^2 +p)/( (√(p^2 +1))))=((p(p+1))/( (√(p^2 +1))))>p but p−1<p ⇒f(p)≠p−1 ⇒no solution for f(p)=p−1
$${f}'\left({x}\right)=\left({px}+\sqrt{{px}}\right)\left(−\frac{{p}}{\mathrm{2}\left({px}+\mathrm{1}\right)\sqrt{{px}+\mathrm{1}}}\right)+\frac{\mathrm{1}}{\:\sqrt{{px}+\mathrm{1}}}\left({p}+\frac{{p}}{\mathrm{2}\sqrt{{px}}}\right) \\ $$$${f}'\left({x}\right)=\frac{{p}}{\mathrm{2}}\left[−\frac{\sqrt{{px}}}{{px}+\mathrm{1}}+\frac{\mathrm{1}}{\:\sqrt{{px}}}\right] \\ $$$${f}'\left({x}\right)=\frac{{p}}{\mathrm{2}\left({px}+\mathrm{1}\right)\sqrt{{px}}} \\ $$$${f}'\left({x}\right)\:>\mathrm{0}\:{if}\:{p}>\mathrm{0} \\ $$$${f}'\left({x}\right)\:<\mathrm{0}\:{if}\:{p}<\mathrm{0} \\ $$$${i}.{e}.\:{f}\left({x}\right)\:{is}\:{always}\:{increasing}\:{or} \\ $$$${always}\:{decreasing}. \\ $$$${i}.{e}.\:{if}\:{f}\left({a}\right)={f}\left({b}\right)\Rightarrow{a}={b}\Rightarrow\frac{{a}}{{b}}=\mathrm{1} \\ $$$$ \\ $$$${f}\left({p}\right)=\frac{{p}^{\mathrm{2}} +{p}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}=\frac{{p}\left({p}+\mathrm{1}\right)}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}>{p} \\ $$$${but}\:{p}−\mathrm{1}<{p} \\ $$$$\Rightarrow{f}\left({p}\right)\neq{p}−\mathrm{1} \\ $$$$\Rightarrow{no}\:{solution}\:{for}\:{f}\left({p}\right)={p}−\mathrm{1} \\ $$
Commented by behi83417@gmail.com last updated on 27/Jun/18
dear master!great job done by you. thanks in advance. is there any chance to find f^(−1) (x)?
$${dear}\:{master}!{great}\:{job}\:{done}\:{by}\:{you}. \\ $$$${thanks}\:{in}\:{advance}. \\ $$$${is}\:{there}\:{any}\:{chance}\:{to}\:{find}\:\boldsymbol{{f}}^{−\mathrm{1}} \left(\boldsymbol{{x}}\right)? \\ $$
Commented by MrW3 last updated on 27/Jun/18
I see no chance to find f^(−1) (x).
$${I}\:{see}\:{no}\:{chance}\:{to}\:{find}\:{f}^{−\mathrm{1}} \left({x}\right). \\ $$
Commented by ajfour last updated on 27/Jun/18
Can we find θ if sin θ(1+tan θ)=c ?
$${Can}\:{we}\:{find}\:\theta\:{if} \\ $$$$\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{tan}\:\theta\right)={c}\:\:\:\:\:? \\ $$
Commented by behi83417@gmail.com last updated on 27/Jun/18
no,i think. by putting: px=tg^2 𝛉,we have the equation: sin𝛉(1+tg𝛉)=y and solving this, not easy.
$${no},{i}\:{think}. \\ $$$${by}\:{putting}:\:\boldsymbol{{px}}=\boldsymbol{{tg}}^{\mathrm{2}} \boldsymbol{\theta},{we}\:{have}\:{the} \\ $$$${equation}:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{sin}\theta}\left(\mathrm{1}+\boldsymbol{{tg}\theta}\right)=\boldsymbol{{y}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{solving}}\:\boldsymbol{{this}},\:{not}\:{easy}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *