Question Number 38593 by ajfour last updated on 27/Jun/18

Commented by ajfour last updated on 27/Jun/18
$${Find}\:\theta\:{in}\:{terms}\:{of}\:\boldsymbol{{c}}\:. \\ $$
Commented by MrW3 last updated on 27/Jun/18
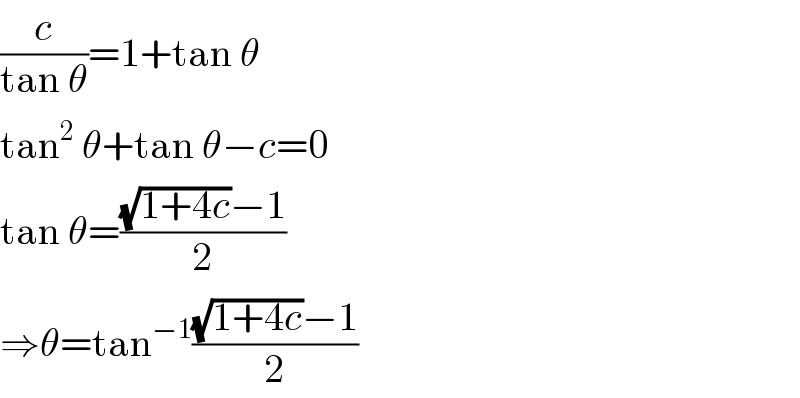
$$\frac{{c}}{\mathrm{tan}\:\theta}=\mathrm{1}+\mathrm{tan}\:\theta \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{tan}\:\theta−{c}=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta=\frac{\sqrt{\mathrm{1}+\mathrm{4}{c}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{1}+\mathrm{4}{c}}−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 27/Jun/18

$${thank}\:{you}\:{Sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
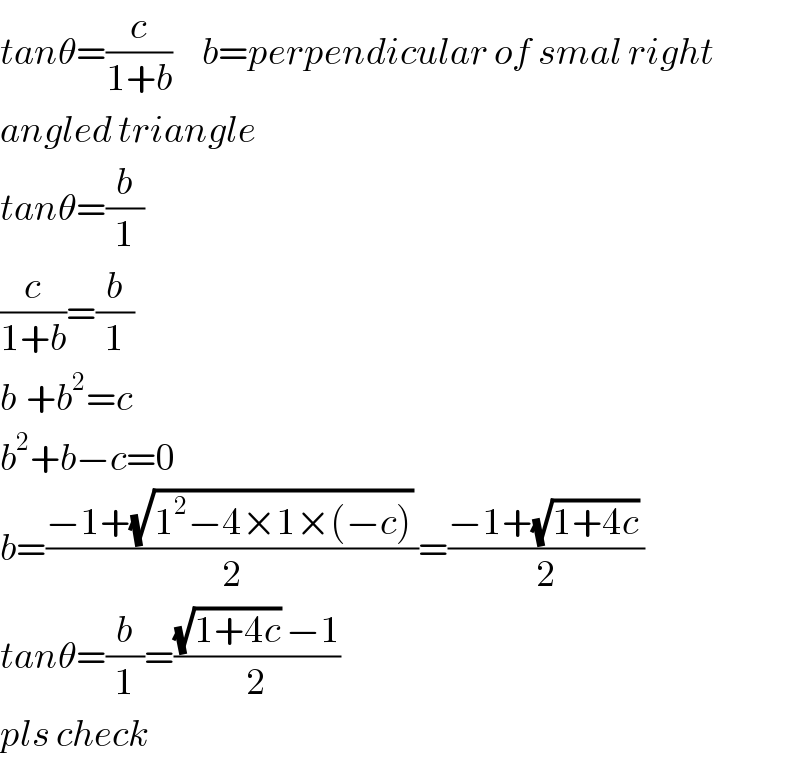
$${tan}\theta=\frac{{c}}{\mathrm{1}+{b}}\:\:\:\:\:{b}={perpendicular}\:{of}\:{smal}\:{right} \\ $$$${angled}\:{triangle} \\ $$$${tan}\theta=\frac{{b}}{\mathrm{1}} \\ $$$$\frac{{c}}{\mathrm{1}+{b}}=\frac{{b}}{\mathrm{1}}\:\: \\ $$$${b}^{} +{b}^{\mathrm{2}} ={c} \\ $$$${b}^{\mathrm{2}} +{b}−{c}=\mathrm{0} \\ $$$${b}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}^{\mathrm{2}} −\mathrm{4}×\mathrm{1}×\left(−{c}\right)}\:}{\mathrm{2}}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{c}}\:}{\mathrm{2}} \\ $$$${tan}\theta=\frac{{b}}{\mathrm{1}}=\frac{\sqrt{\mathrm{1}+\mathrm{4}{c}}\:−\mathrm{1}}{\mathrm{2}} \\ $$$${pls}\:{check} \\ $$
Commented by ajfour last updated on 27/Jun/18
$${Thank}\:{you}\:{Sir},\:{but}\:{i}\:{think}\:{the} \\ $$$${next}\:{question}\:{is}\:{bit}\:{challenging}! \\ $$
