Menu Close

Question-38600

Tinku Tara 0 Comments
Pin




Question Number 38600 by ajfour last updated on 27/Jun/18
Commented by ajfour last updated on 27/Jun/18
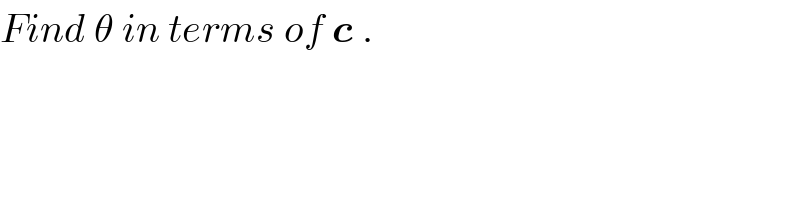
Find θ in terms of c .
$${Find}\:\theta\:{in}\:{terms}\:{of}\:\boldsymbol{{c}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jun/18
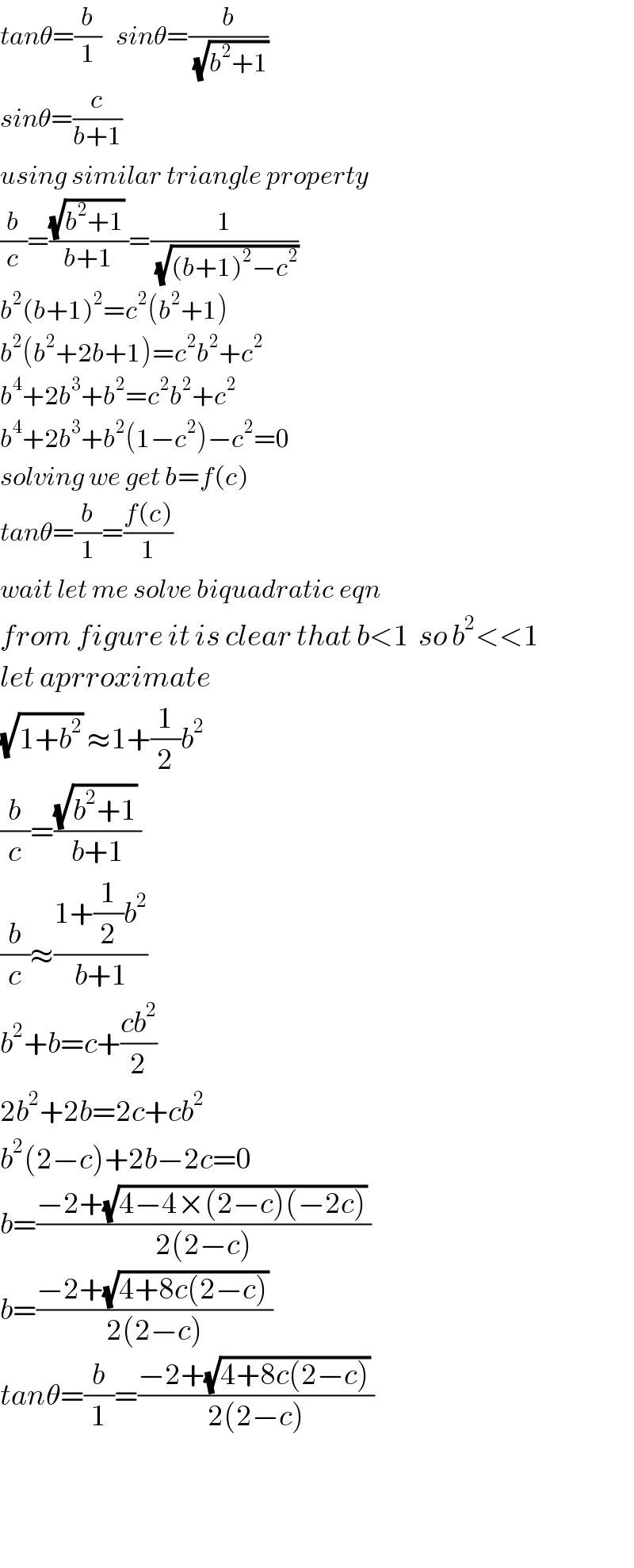
tanθ=(b/1) sinθ=(b/( (√(b^2 +1)))) sinθ=(c/(b+1)) using similar triangle property (b/c)=(((√(b^2 +1)) )/(b+1))=(1/( (√((b+1)^2 −c^2 )))) b^2 (b+1)^2 =c^2 (b^2 +1) b^2 (b^2 +2b+1)=c^2 b^2 +c^2 b^4 +2b^3 +b^2 =c^2 b^2 +c^2 b^4 +2b^3 +b^2 (1−c^2 )−c^2 =0 solving we get b=f(c) tanθ=(b/1)=((f(c))/1) wait let me solve biquadratic eqn from figure it is clear that b<1 so b^2 <<1 let aprroximate (√(1+b^2 )) ≈1+(1/2)b^2 (b/c)=(((√(b^2 +1)) )/(b+1)) (b/c)≈((1+(1/2)b^2 )/(b+1)) b^2 +b=c+((cb^2 )/2) 2b^2 +2b=2c+cb^2 b^2 (2−c)+2b−2c=0 b=((−2+(√(4−4×(2−c)(−2c))) )/(2(2−c))) b=((−2+(√(4+8c(2−c))) )/(2(2−c))) tanθ=(b/1)=((−2+(√(4+8c(2−c))) )/(2(2−c)))
$${tan}\theta=\frac{{b}}{\mathrm{1}}\:\:\:{sin}\theta=\frac{{b}}{\:\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${sin}\theta=\frac{{c}}{{b}+\mathrm{1}} \\ $$$${using}\:{similar}\:{triangle}\:{property} \\ $$$$\frac{{b}}{{c}}=\frac{\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}\:}{{b}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\left({b}+\mathrm{1}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }} \\ $$$${b}^{\mathrm{2}} \left({b}+\mathrm{1}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${b}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\right)={c}^{\mathrm{2}} {b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$${b}^{\mathrm{4}} +\mathrm{2}{b}^{\mathrm{3}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} {b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$${b}^{\mathrm{4}} +\mathrm{2}{b}^{\mathrm{3}} +{b}^{\mathrm{2}} \left(\mathrm{1}−{c}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${solving}\:{we}\:{get}\:{b}={f}\left({c}\right) \\ $$$${tan}\theta=\frac{{b}}{\mathrm{1}}=\frac{{f}\left({c}\right)}{\mathrm{1}} \\ $$$${wait}\:{let}\:{me}\:{solve}\:{biquadratic}\:{eqn} \\ $$$${from}\:{figure}\:{it}\:{is}\:{clear}\:{that}\:{b}<\mathrm{1}\:\:{so}\:{b}^{\mathrm{2}} <<\mathrm{1} \\ $$$${let}\:{aprroximate} \\ $$$$\sqrt{\mathrm{1}+{b}^{\mathrm{2}} }\:\approx\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} \\ $$$$\frac{{b}}{{c}}=\frac{\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}\:}{{b}+\mathrm{1}} \\ $$$$\frac{{b}}{{c}}\approx\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{b}^{\mathrm{2}} }{{b}+\mathrm{1}} \\ $$$${b}^{\mathrm{2}} +{b}={c}+\frac{{cb}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{b}=\mathrm{2}{c}+{cb}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \left(\mathrm{2}−{c}\right)+\mathrm{2}{b}−\mathrm{2}{c}=\mathrm{0} \\ $$$${b}=\frac{−\mathrm{2}+\sqrt{\mathrm{4}−\mathrm{4}×\left(\mathrm{2}−{c}\right)\left(−\mathrm{2}{c}\right)}\:}{\mathrm{2}\left(\mathrm{2}−{c}\right)} \\ $$$${b}=\frac{−\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{8}{c}\left(\mathrm{2}−{c}\right)}\:}{\mathrm{2}\left(\mathrm{2}−{c}\right)} \\ $$$${tan}\theta=\frac{{b}}{\mathrm{1}}=\frac{−\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{8}{c}\left(\mathrm{2}−{c}\right)}\:}{\mathrm{2}\left(\mathrm{2}−{c}\right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by behi83417@gmail.com last updated on 27/Jun/18
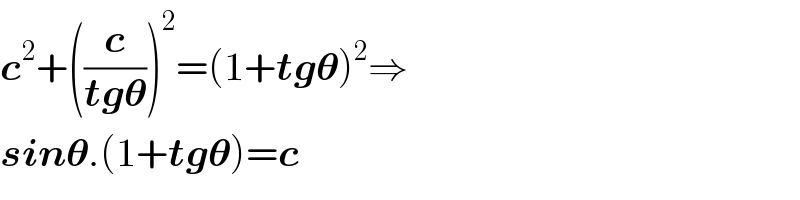
c^2 +((c/(tg𝛉)))^2 =(1+tg𝛉)^2 ⇒ sin𝛉.(1+tg𝛉)=c
$$\boldsymbol{{c}}^{\mathrm{2}} +\left(\frac{\boldsymbol{{c}}}{\boldsymbol{{tg}\theta}}\right)^{\mathrm{2}} =\left(\mathrm{1}+\boldsymbol{{tg}\theta}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\boldsymbol{{sin}\theta}.\left(\mathrm{1}+\boldsymbol{{tg}\theta}\right)=\boldsymbol{{c}}\: \\ $$
Answered by MJS last updated on 28/Jun/18
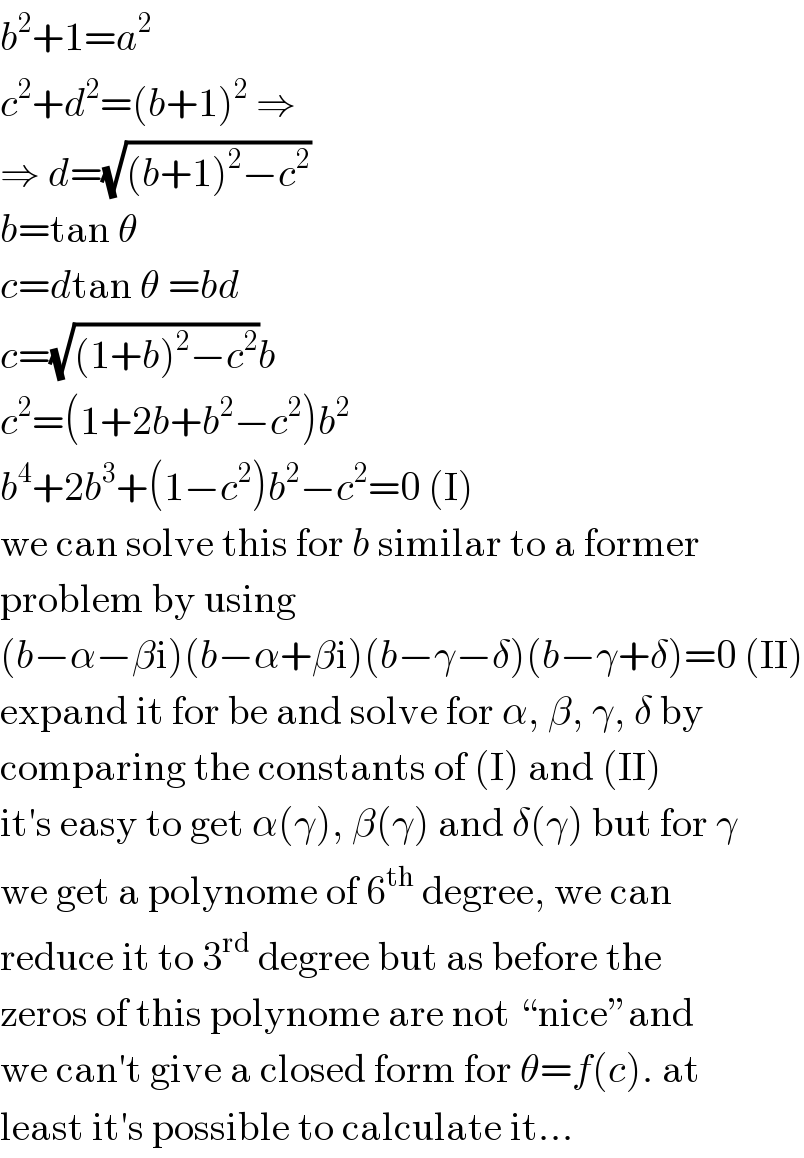
b^2 +1=a^2 c^2 +d^2 =(b+1)^2 ⇒ ⇒ d=(√((b+1)^2 −c^2 )) b=tan θ c=dtan θ =bd c=(√((1+b)^2 −c^2 ))b c^2 =(1+2b+b^2 −c^2 )b^2 b^4 +2b^3 +(1−c^2 )b^2 −c^2 =0 (I) we can solve this for b similar to a former problem by using (b−α−βi)(b−α+βi)(b−γ−δ)(b−γ+δ)=0 (II) expand it for be and solve for α, β, γ, δ by comparing the constants of (I) and (II) it′s easy to get α(γ), β(γ) and δ(γ) but for γ we get a polynome of 6^(th) degree, we can reduce it to 3^(rd) degree but as before the zeros of this polynome are not “nice”and we can′t give a closed form for θ=f(c). at least it′s possible to calculate it...
$${b}^{\mathrm{2}} +\mathrm{1}={a}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\left({b}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\Rightarrow\:{d}=\sqrt{\left({b}+\mathrm{1}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$${b}=\mathrm{tan}\:\theta \\ $$$${c}={d}\mathrm{tan}\:\theta\:={bd} \\ $$$${c}=\sqrt{\left(\mathrm{1}+{b}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} }{b} \\ $$$${c}^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{2}{b}+{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} \\ $$$${b}^{\mathrm{4}} +\mathrm{2}{b}^{\mathrm{3}} +\left(\mathrm{1}−{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0}\:\left(\mathrm{I}\right) \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{b}\:\mathrm{similar}\:\mathrm{to}\:\mathrm{a}\:\mathrm{former} \\ $$$$\mathrm{problem}\:\mathrm{by}\:\mathrm{using} \\ $$$$\left({b}−\alpha−\beta\mathrm{i}\right)\left({b}−\alpha+\beta\mathrm{i}\right)\left({b}−\gamma−\delta\right)\left({b}−\gamma+\delta\right)=\mathrm{0}\:\left(\mathrm{II}\right) \\ $$$$\mathrm{expand}\:\mathrm{it}\:\mathrm{for}\:\mathrm{be}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:\alpha,\:\beta,\:\gamma,\:\delta\:\mathrm{by} \\ $$$$\mathrm{comparing}\:\mathrm{the}\:\mathrm{constants}\:\mathrm{of}\:\left(\mathrm{I}\right)\:\mathrm{and}\:\left(\mathrm{II}\right) \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{get}\:\alpha\left(\gamma\right),\:\beta\left(\gamma\right)\:\mathrm{and}\:\delta\left(\gamma\right)\:\mathrm{but}\:\mathrm{for}\:\gamma \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{degree},\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{reduce}\:\mathrm{it}\:\mathrm{to}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{but}\:\mathrm{as}\:\mathrm{before}\:\mathrm{the} \\ $$$$\mathrm{zeros}\:\mathrm{of}\:\mathrm{this}\:\mathrm{polynome}\:\mathrm{are}\:\mathrm{not}\:“\mathrm{nice}''\mathrm{and} \\ $$$$\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{give}\:\mathrm{a}\:\mathrm{closed}\:\mathrm{form}\:\mathrm{for}\:\theta={f}\left({c}\right).\:\mathrm{at} \\ $$$$\mathrm{least}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{it}… \\ $$
Commented by MJS last updated on 28/Jun/18
b^4 +2b^3 +(1−c^2 )b^2 −c^2 =0 b^4 −2(α+γ)b^3 +(α^2 +4αγ+β^2 +γ^2 −δ^2 )b^2 −2(α^2 γ+αγ^2 −αδ^2 +β^2 γ)b+(α^2 +β^2 )(γ^2 −δ^2 )=0 (1) α+γ+1=0 (2) α^2 +4αγ+β^2 +γ^2 −δ^2 −1+c^2 =0 (3) α^2 γ+αγ^2 −αδ^2 +β^2 γ=0 (4) α^2 γ^2 −α^2 δ^2 +β^2 γ^2 −β^2 δ^2 +c^2 =0 (1) α=−γ−1 (2) β^2 −2γ^2 −2γ−δ^2 +c^2 =0 ⇒ β=(√(2γ^2 +2γ+δ^2 −c^2 )) (3) 2γ^3 +3γ^2 +2γδ^2 +(1−c^2 )γ+δ^2 =0 ⇒ ⇒ δ=(√((γ(−2γ^2 −3γ−1+c^2 ))/(2γ+1))) (4) ((16γ^6 +48γ^5 −8(c^2 −7)γ^4 −16(c^2 −2)γ^3 +(c^2 −3)^2 γ^2 +(c^2 +1)^2 γ+c^2 )/((2γ+1)^2 ))=0e γ^6 +3γ^5 −((c^2 −7)/2)γ^4 −(c^2 −2)γ^3 +(((c^2 −3)^2 )/(16))γ^2 +(((c^2 +1)^2 )/(16))γ+(c^2 /(16))=0 γ=u−(1/2) u^6 −((2c^2 −1)/4)u^4 +((c^2 (c^2 +6))/(16))u^2 −(c^4 /(64))=0 u=(√v) v^3 −((2c^2 −1)/4)v^2 +((c^2 (c^2 +6))/(16))v−(c^4 /(64))=0 v=w+((2c^2 −1)/(12)) w^3 −((c^4 −14c^2 +1)/(48))+((c^6 +33c^4 +21c^2 −1)/(864))=0 p=−((c^4 −14c^2 +1)/(48)); q=((c^6 +33c^4 +21c^2 −1)/(864)) m=((−(q/2)+(√((q^2 /4)+(p^3 /(27))))))^(1/3) ; n=((−(q/2)+(√((q^2 /4)+(p^3 /(27))))))^(1/3) = w_1 =m+n w_2 =(−(1/2)+((√3)/2)i)m+(−(1/2)−((√3)/2)i)n w_3 =(−(1/2)−((√3)/2)i)m+(−(1/2)+((√3)/2)i)n v_i =w_i +((2c^2 −1)/(12)) u_i =(√v_i ) γ_i =u_i −(1/2) α_i =−γ_i −1 β_i =(√((2γ_i ^3 +3γ_i ^2 +(1−c^2 )γ_i −c^2 )/(2γ_i +1))) δ_i =(√((γ_i (−2γ_i ^2 −3γ_i −1+c^2 ))/(2γ_i +1))) b=α_i ±β_i i ∨ γ_i ±δ_i θ=arctan b
$${b}^{\mathrm{4}} +\mathrm{2}{b}^{\mathrm{3}} +\left(\mathrm{1}−{c}^{\mathrm{2}} \right){b}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${b}^{\mathrm{4}} −\mathrm{2}\left(\alpha+\gamma\right){b}^{\mathrm{3}} +\left(\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \right){b}^{\mathrm{2}} −\mathrm{2}\left(\alpha^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} −\alpha\delta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma\right){b}+\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:\alpha+\gamma+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} −\mathrm{1}+{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:\alpha^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} −\alpha\delta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:\alpha^{\mathrm{2}} \gamma^{\mathrm{2}} −\alpha^{\mathrm{2}} \delta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma^{\mathrm{2}} −\beta^{\mathrm{2}} \delta^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:\alpha=−\gamma−\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\:\beta^{\mathrm{2}} −\mathrm{2}\gamma^{\mathrm{2}} −\mathrm{2}\gamma−\delta^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:\beta=\sqrt{\mathrm{2}\gamma^{\mathrm{2}} +\mathrm{2}\gamma+\delta^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\left(\mathrm{3}\right)\:\:\mathrm{2}\gamma^{\mathrm{3}} +\mathrm{3}\gamma^{\mathrm{2}} +\mathrm{2}\gamma\delta^{\mathrm{2}} +\left(\mathrm{1}−{c}^{\mathrm{2}} \right)\gamma+\delta^{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\delta=\sqrt{\frac{\gamma\left(−\mathrm{2}\gamma^{\mathrm{2}} −\mathrm{3}\gamma−\mathrm{1}+{c}^{\mathrm{2}} \right)}{\mathrm{2}\gamma+\mathrm{1}}} \\ $$$$\left(\mathrm{4}\right)\:\:\frac{\mathrm{16}\gamma^{\mathrm{6}} +\mathrm{48}\gamma^{\mathrm{5}} −\mathrm{8}\left({c}^{\mathrm{2}} −\mathrm{7}\right)\gamma^{\mathrm{4}} −\mathrm{16}\left({c}^{\mathrm{2}} −\mathrm{2}\right)\gamma^{\mathrm{3}} +\left({c}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} \gamma^{\mathrm{2}} +\left({c}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \gamma+{c}^{\mathrm{2}} }{\left(\mathrm{2}\gamma+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0}{e} \\ $$$$ \\ $$$$\gamma^{\mathrm{6}} +\mathrm{3}\gamma^{\mathrm{5}} −\frac{{c}^{\mathrm{2}} −\mathrm{7}}{\mathrm{2}}\gamma^{\mathrm{4}} −\left({c}^{\mathrm{2}} −\mathrm{2}\right)\gamma^{\mathrm{3}} +\frac{\left({c}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{16}}\gamma^{\mathrm{2}} +\frac{\left({c}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{16}}\gamma+\frac{{c}^{\mathrm{2}} }{\mathrm{16}}=\mathrm{0} \\ $$$$\gamma={u}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${u}^{\mathrm{6}} −\frac{\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}{u}^{\mathrm{4}} +\frac{{c}^{\mathrm{2}} \left({c}^{\mathrm{2}} +\mathrm{6}\right)}{\mathrm{16}}{u}^{\mathrm{2}} −\frac{{c}^{\mathrm{4}} }{\mathrm{64}}=\mathrm{0} \\ $$$${u}=\sqrt{{v}} \\ $$$${v}^{\mathrm{3}} −\frac{\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}{v}^{\mathrm{2}} +\frac{{c}^{\mathrm{2}} \left({c}^{\mathrm{2}} +\mathrm{6}\right)}{\mathrm{16}}{v}−\frac{{c}^{\mathrm{4}} }{\mathrm{64}}=\mathrm{0} \\ $$$${v}={w}+\frac{\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{12}} \\ $$$${w}^{\mathrm{3}} −\frac{{c}^{\mathrm{4}} −\mathrm{14}{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{48}}+\frac{{c}^{\mathrm{6}} +\mathrm{33}{c}^{\mathrm{4}} +\mathrm{21}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{864}}=\mathrm{0} \\ $$$${p}=−\frac{{c}^{\mathrm{4}} −\mathrm{14}{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{48}};\:{q}=\frac{{c}^{\mathrm{6}} +\mathrm{33}{c}^{\mathrm{4}} +\mathrm{21}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{864}} \\ $$$${m}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}};\:{n}=\sqrt[{\mathrm{3}}]{−\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}}= \\ $$$${w}_{\mathrm{1}} ={m}+{n} \\ $$$${w}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){m}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){n} \\ $$$${w}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){m}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right){n} \\ $$$${v}_{{i}} ={w}_{{i}} +\frac{\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}}{\mathrm{12}} \\ $$$${u}_{{i}} =\sqrt{{v}_{{i}} } \\ $$$$\gamma_{{i}} ={u}_{{i}} −\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\alpha_{{i}} =−\gamma_{{i}} −\mathrm{1} \\ $$$$\beta_{{i}} =\sqrt{\frac{\mathrm{2}\gamma_{{i}} ^{\mathrm{3}} +\mathrm{3}\gamma_{{i}} ^{\mathrm{2}} +\left(\mathrm{1}−{c}^{\mathrm{2}} \right)\gamma_{{i}} −{c}^{\mathrm{2}} }{\mathrm{2}\gamma_{{i}} +\mathrm{1}}} \\ $$$$\delta_{{i}} =\sqrt{\frac{\gamma_{{i}} \left(−\mathrm{2}\gamma_{{i}} ^{\mathrm{2}} −\mathrm{3}\gamma_{{i}} −\mathrm{1}+{c}^{\mathrm{2}} \right)}{\mathrm{2}\gamma_{{i}} +\mathrm{1}}} \\ $$$${b}=\alpha_{{i}} \pm\beta_{{i}} \mathrm{i}\:\vee\:\gamma_{{i}} \pm\delta_{{i}} \\ $$$$\theta=\mathrm{arctan}\:{b} \\ $$
Commented by ajfour last updated on 29/Jun/18
I undestand Sir,plentiful thanks!
$${I}\:{undestand}\:{Sir},{plentiful}\:{thanks}! \\ $$
Commented by MJS last updated on 29/Jun/18
I tried several ways but they all lead to the same equation...
$$\mathrm{I}\:\mathrm{tried}\:\mathrm{several}\:\mathrm{ways}\:\mathrm{but}\:\mathrm{they}\:\mathrm{all}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{equation}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *