Question Number 38707 by Rio Mike last updated on 28/Jun/18
Commented by Rio Mike last updated on 28/Jun/18

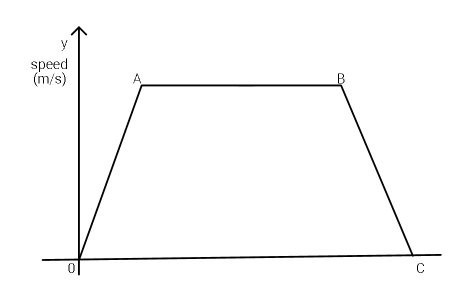
$${The}\:{figure}\:{above}\:{shows}\:{the}\:{speed}\:{time} \\ $$$${graph}\:{for}\:{a}\:{train}\:{journey}.{OA},{AB} \\ $$$${and}\:{BC}\:{are}\:{parts}\:{of}\:{the}\:{line}\:{whose} \\ $$$${equations}\:{are}\: \\ $$$${y}\:=\:\frac{\mathrm{16}}{\mathrm{45}\:}{x},\:{y}\:=\:\mathrm{16}\:{and}\:\frac{{x}}{\mathrm{180}}\:+\:\frac{{y}}{\mathrm{48}}\:=\:\mathrm{1}. \\ $$$${respectively}. \\ $$$${Calculate}\:: \\ $$$$\left.{a}\right)\:{the}\:{coordinates}\:{of}\:{A},{B},{C} \\ $$$$\left.{b}\right)\:{the}\:{length}\:{of}\:{time}\:{for}\:{which}\:{the} \\ $$$${speed}\:{is}\:{constand}. \\ $$$$\left.{c}\right)\:{The}\:{total}\:{distance}\:{travelled}\:{by} \\ $$$${the}\:{train}. \\ $$
Commented by MJS last updated on 28/Jun/18

$${l}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{16}}{\mathrm{45}}{x};\:{l}_{\mathrm{2}} \left({x}\right)=\mathrm{16};\:{l}_{\mathrm{3}} \left({x}\right)=\mathrm{48}−\frac{\mathrm{4}}{\mathrm{15}}{x} \\ $$$${a}.\:\:{A}={l}_{\mathrm{1}} \cap{l}_{\mathrm{2}} =\begin{pmatrix}{{x}_{{A}} }\\{\mathrm{16}}\end{pmatrix};\:{B}={l}_{\mathrm{2}} \cap{l}_{\mathrm{3}} =\begin{pmatrix}{{x}_{{B}} }\\{\mathrm{16}}\end{pmatrix};\:{C}=\mathrm{zero}\left({l}_{\mathrm{3}} \right)=\begin{pmatrix}{{x}_{{C}} }\\{\mathrm{0}}\end{pmatrix} \\ $$$${b}.\:\:\mid{B}−{C}\mid={x}_{{C}} −{x}_{{B}} \\ $$$${c}.\:\:\underset{\mathrm{0}} {\overset{{x}_{{A}} } {\int}}{l}_{\mathrm{1}} {dx}+\underset{{x}_{{A}} } {\overset{{x}_{{B}} } {\int}}{l}_{\mathrm{2}} {dx}+\underset{{x}_{{B}} } {\overset{{x}_{{C}} } {\int}}{l}_{\mathrm{3}} {dx} \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{the}\:\mathrm{work}\:\mathrm{if}\:\mathrm{possible}\:\mathrm{and}\:\mathrm{let}\:\mathrm{me} \\ $$$$\mathrm{know}\:\mathrm{where}\:\mathrm{you}'\mathrm{re}\:\mathrm{in}\:\mathrm{trouble}.\:\mathrm{this}\:\mathrm{should} \\ $$$$\mathrm{be}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{job} \\ $$
Commented by Rio Mike last updated on 28/Jun/18

$${sure}\:{thanks} \\ $$
