Question Number 38825 by Sr@2004 last updated on 30/Jun/18
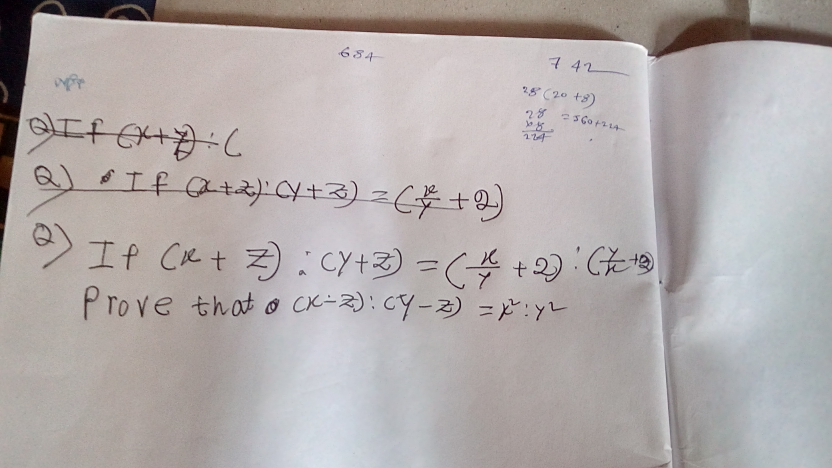
Commented by kunal1234523 last updated on 30/Jun/18
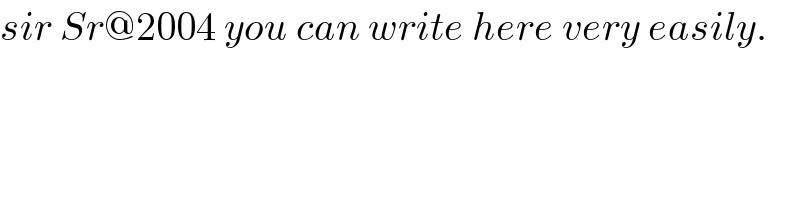
$${sir}\:{Sr}@\mathrm{2004}\:{you}\:{can}\:{write}\:{here}\:{very}\:{easily}. \\ $$
Commented by Sr@2004 last updated on 30/Jun/18

$${please}\:{solve}\:{it}. \\ $$
Commented by NECx last updated on 30/Jun/18
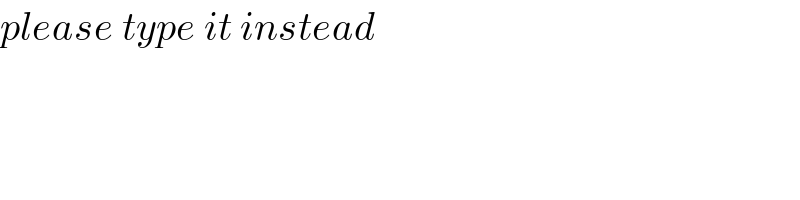
$${please}\:{type}\:{it}\:{instead} \\ $$
Commented by Sr@2004 last updated on 30/Jun/18
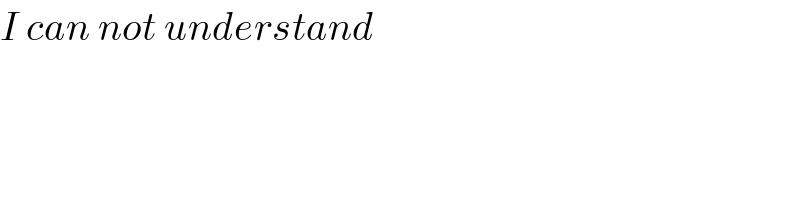
$${I}\:{can}\:{not}\:{understand} \\ $$
Answered by kunal1234523 last updated on 30/Jun/18
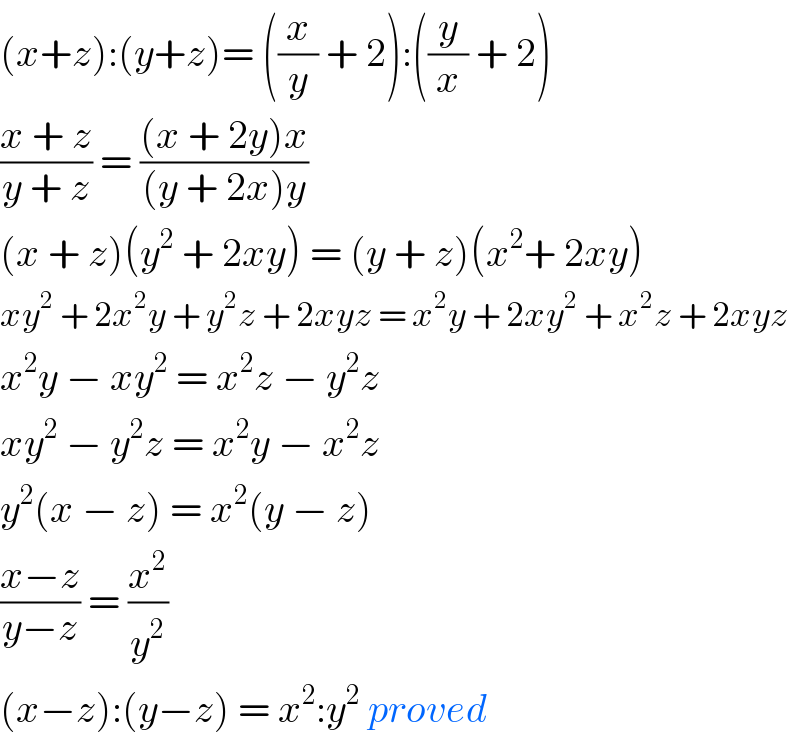
$$\left({x}+{z}\right):\left({y}+{z}\right)=\:\left(\frac{{x}}{{y}}\:+\:\mathrm{2}\right):\left(\frac{{y}}{{x}}\:+\:\mathrm{2}\right) \\ $$$$\frac{{x}\:+\:{z}}{{y}\:+\:{z}}\:=\:\frac{\left({x}\:+\:\mathrm{2}{y}\right){x}}{\left({y}\:+\:\mathrm{2}{x}\right){y}} \\ $$$$\left({x}\:+\:{z}\right)\left({y}^{\mathrm{2}} \:+\:\mathrm{2}{xy}\right)\:=\:\left({y}\:+\:{z}\right)\left({x}^{\mathrm{2}} +\:\mathrm{2}{xy}\right) \\ $$$${xy}^{\mathrm{2}} \:+\:\mathrm{2}{x}^{\mathrm{2}} {y}\:+\:{y}^{\mathrm{2}} {z}\:+\:\mathrm{2}{xyz}\:=\:{x}^{\mathrm{2}} {y}\:+\:\mathrm{2}{xy}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} {z}\:+\:\mathrm{2}{xyz} \\ $$$${x}^{\mathrm{2}} {y}\:−\:{xy}^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} {z}\:−\:{y}^{\mathrm{2}} {z} \\ $$$${xy}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} {z}\:=\:{x}^{\mathrm{2}} {y}\:−\:{x}^{\mathrm{2}} {z} \\ $$$${y}^{\mathrm{2}} \left({x}\:−\:{z}\right)\:=\:{x}^{\mathrm{2}} \left({y}\:−\:{z}\right) \\ $$$$\frac{{x}−{z}}{{y}−{z}}\:=\:\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\: \\ $$$$\left({x}−{z}\right):\left({y}−{z}\right)\:=\:{x}^{\mathrm{2}} :{y}^{\mathrm{2}} \:{proved} \\ $$
Commented by Sr@2004 last updated on 30/Jun/18

$${thank}\:{you} \\ $$
Commented by Sr@2004 last updated on 30/Jun/18
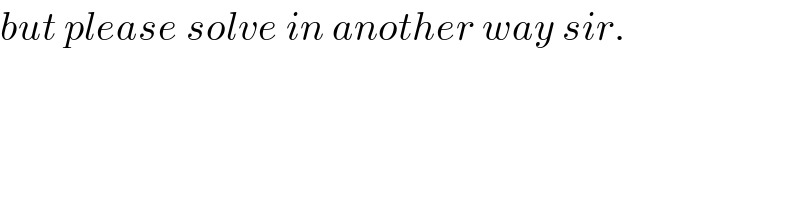
$${but}\:{please}\:{solve}\:{in}\:{another}\:{way}\:{sir}. \\ $$$$ \\ $$
Commented by kunal1234523 last updated on 30/Jun/18

$${in}\:{which}\:{way} \\ $$
