Question Number 38960 by Tinkutara last updated on 01/Jul/18
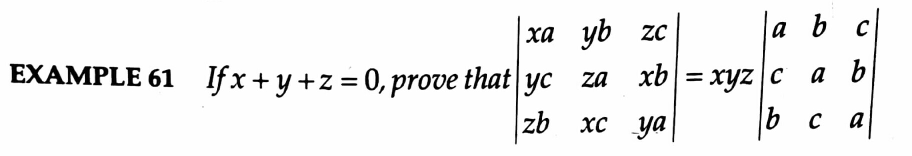
Answered by ajfour last updated on 01/Jul/18
![determinant (((xa),(yb),(zc)),((yc),(za),(xb)),((zb),(xc),(ya)))= xa(a^2 yz−bcx^2 ) +by(b^2 zx−acy^2 )+cz(c^2 xy−abz^2 ) = (a^3 +b^3 +c^3 )xyz−abc(x^3 +y^3 +z^3 ) as x+y+z=0 x^3 +y^3 +z^3 = 3xyz , therefore determinant (((xa),(yb),(zc)),((yc),(za),(xb)),((zb),(xc),(ya)))=xyz(a^3 +b^3 +c^3 −3abc) =xyz[a(a^2 −bc)+b(b^2 −ca)+c(c^2 −ab)] = determinant ((a,b,c),(c,a,b),(b,c,a)) .](https://www.tinkutara.com/question/Q38977.png)
$$\begin{vmatrix}{{xa}}&{{yb}}&{{zc}}\\{{yc}}&{{za}}&{{xb}}\\{{zb}}&{{xc}}&{{ya}}\end{vmatrix}=\:{xa}\left({a}^{\mathrm{2}} {yz}−{bcx}^{\mathrm{2}} \right) \\ $$$$\:+{by}\left({b}^{\mathrm{2}} {zx}−{acy}^{\mathrm{2}} \right)+{cz}\left({c}^{\mathrm{2}} {xy}−{abz}^{\mathrm{2}} \right) \\ $$$$=\:\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right){xyz}−{abc}\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \right) \\ $$$${as}\:\:{x}+{y}+{z}=\mathrm{0} \\ $$$$\:\:\:\:\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} \:=\:\mathrm{3}{xyz}\:\:\:,\:{therefore} \\ $$$$\:\:\begin{vmatrix}{{xa}}&{{yb}}&{{zc}}\\{{yc}}&{{za}}&{{xb}}\\{{zb}}&{{xc}}&{{ya}}\end{vmatrix}={xyz}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}\right) \\ $$$$\:={xyz}\left[{a}\left({a}^{\mathrm{2}} −{bc}\right)+{b}\left({b}^{\mathrm{2}} −{ca}\right)+{c}\left({c}^{\mathrm{2}} −{ab}\right)\right] \\ $$$$\:\:\:=\begin{vmatrix}{{a}}&{{b}}&{{c}}\\{{c}}&{{a}}&{{b}}\\{{b}}&{{c}}&{{a}}\end{vmatrix}\:. \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Commented by ajfour last updated on 01/Jul/18

$${i}\:{have}\:{no}\:{idea}\:{how}\:{to}\:{solve}\:{this} \\ $$$${question},\:{using}\:{the}\:{properties}.. \\ $$
Commented by Tinkutara last updated on 01/Jul/18
Sir why can't we use properties here?
Commented by Tinkutara last updated on 02/Jul/18
OK Sir.
