Menu Close

Question-38967

Tinku Tara 0 Comments
Pin




Question Number 38967 by rahul 19 last updated on 01/Jul/18
Commented by rahul 19 last updated on 01/Jul/18
find V_a −V_b ?
$$\:\mathrm{find}\:\mathrm{V}_{\mathrm{a}} −\mathrm{V}_{\mathrm{b}} \:? \\ $$
Commented by rahul 19 last updated on 01/Jul/18
I' m getting correct ans. by Nodal method but when I do by Parallel grouping of cells , I'm getting wrong ans.
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18
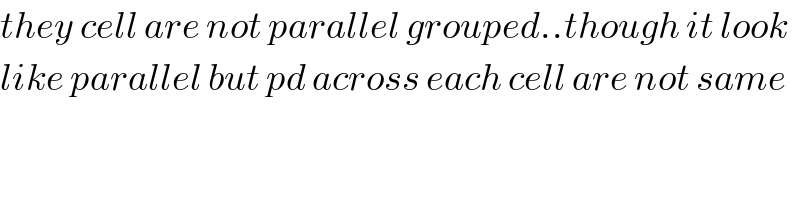
they cell are not parallel grouped..though it look like parallel but pd across each cell are not same
$${they}\:{cell}\:{are}\:{not}\:{parallel}\:{grouped}..{though}\:{it}\:{look}\: \\ $$$${like}\:{parallel}\:{but}\:{pd}\:{across}\:{each}\:{cell}\:{are}\:{not}\:{same} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18
ok but tomorrow...if you want free books to download visit archievs.org...
$${ok}\:{but}\:{tomorrow}…{if}\:{you}\:{want}\:{free}\:{books}\:{to}\: \\ $$$${download}\:{visit}\:{archievs}.{org}… \\ $$
Commented by rahul 19 last updated on 01/Jul/18
Assume R1 internal resistance of E1 and R2 internal resistance of E2. Then all the cells have same P.D , right ? ����
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Jul/18
i have postef theorem related to cells ...pls purchaze resnik and haliday and dc pandey books...i hav read lot of physics books but resnik haliday for concept and pandey for problems good.. as per your question if internal resistance then parallel
$${i}\:{have}\:{postef}\:{theorem}\:{related}\:{to}\:{cells}\:…{pls}\:\:{purchaze} \\ $$$${resnik}\:{and}\:{haliday}\:{and}\:{dc}\:{pandey}\:{books}…{i}\:{hav} \\ $$$${read}\:{lot}\:{of}\:{physics}\:{books}\:{but}\:{resnik}\:{haliday} \\ $$$${for}\:{concept}\:{and}\:{pandey}\:{for}\:{problems}\:{good}.. \\ $$$${as}\:{per}\:{your}\:{question}\:{if}\:{internal}\:{resistance}\:{then} \\ $$$${parallel} \\ $$$$ \\ $$
Commented by rahul 19 last updated on 01/Jul/18
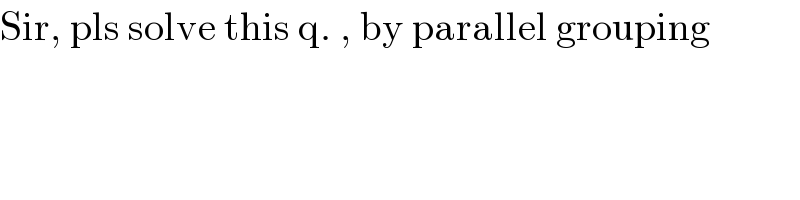
Sir, pls solve this q. , by parallel grouping
$$\mathrm{Sir},\:\mathrm{pls}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{q}.\:,\:\mathrm{by}\:\mathrm{parallel}\:\mathrm{grouping} \\ $$
Commented by rahul 19 last updated on 02/Jul/18
???
$$??? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jul/18
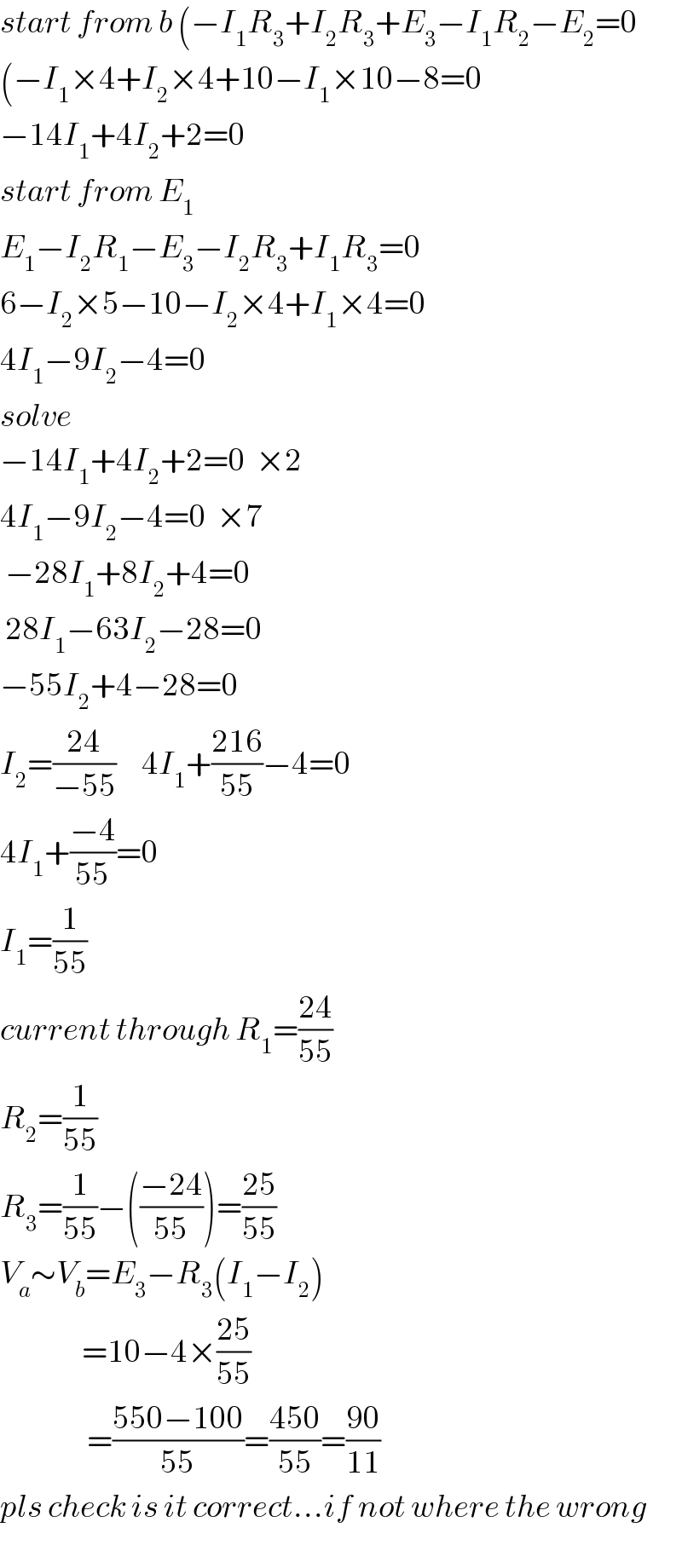
start from b (−I_1 R_3 +I_2 R_3 +E_3 −I_1 R_2 −E_2 =0 (−I_1 ×4+I_2 ×4+10−I_1 ×10−8=0 −14I_1 +4I_2 +2=0 start from E_1 E_1 −I_2 R_1 −E_3 −I_2 R_3 +I_1 R_3 =0 6−I_2 ×5−10−I_2 ×4+I_1 ×4=0 4I_1 −9I_2 −4=0 solve −14I_1 +4I_2 +2=0 ×2 4I_1 −9I_2 −4=0 ×7 −28I_1 +8I_2 +4=0 28I_1 −63I_2 −28=0 −55I_2 +4−28=0 I_2 =((24)/(−55)) 4I_1 +((216)/(55))−4=0 4I_1 +((−4)/(55))=0 I_1 =(1/(55)) current through R_1 =((24)/(55)) R_2 =(1/(55)) R_3 =(1/(55))−(((−24)/(55)))=((25)/(55)) V_a ∼V_b =E_3 −R_3 (I_1 −I_2 ) =10−4×((25)/(55)) =((550−100)/(55))=((450)/(55))=((90)/(11)) pls check is it correct...if not where the wrong
$${start}\:{from}\:{b}\:\left(−{I}_{\mathrm{1}} {R}_{\mathrm{3}} +{I}_{\mathrm{2}} {R}_{\mathrm{3}} +{E}_{\mathrm{3}} −{I}_{\mathrm{1}} {R}_{\mathrm{2}} −{E}_{\mathrm{2}} =\mathrm{0}\right. \\ $$$$\left(−{I}_{\mathrm{1}} ×\mathrm{4}+{I}_{\mathrm{2}} ×\mathrm{4}+\mathrm{10}−{I}_{\mathrm{1}} ×\mathrm{10}−\mathrm{8}=\mathrm{0}\right. \\ $$$$−\mathrm{14}{I}_{\mathrm{1}} +\mathrm{4}{I}_{\mathrm{2}} +\mathrm{2}=\mathrm{0} \\ $$$${start}\:{from}\:{E}_{\mathrm{1}} \\ $$$${E}_{\mathrm{1}} −{I}_{\mathrm{2}} {R}_{\mathrm{1}} −{E}_{\mathrm{3}} −{I}_{\mathrm{2}} {R}_{\mathrm{3}} +{I}_{\mathrm{1}} {R}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{6}−{I}_{\mathrm{2}} ×\mathrm{5}−\mathrm{10}−{I}_{\mathrm{2}} ×\mathrm{4}+{I}_{\mathrm{1}} ×\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}{I}_{\mathrm{1}} −\mathrm{9}{I}_{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$${solve}\: \\ $$$$−\mathrm{14}{I}_{\mathrm{1}} +\mathrm{4}{I}_{\mathrm{2}} +\mathrm{2}=\mathrm{0}\:\:×\mathrm{2} \\ $$$$\mathrm{4}{I}_{\mathrm{1}} −\mathrm{9}{I}_{\mathrm{2}} −\mathrm{4}=\mathrm{0}\:\:×\mathrm{7} \\ $$$$\:−\mathrm{28}{I}_{\mathrm{1}} +\mathrm{8}{I}_{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\:\mathrm{28}{I}_{\mathrm{1}} −\mathrm{63}{I}_{\mathrm{2}} −\mathrm{28}=\mathrm{0} \\ $$$$−\mathrm{55}{I}_{\mathrm{2}} +\mathrm{4}−\mathrm{28}=\mathrm{0} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{24}}{−\mathrm{55}}\:\:\:\:\:\mathrm{4}{I}_{\mathrm{1}} +\frac{\mathrm{216}}{\mathrm{55}}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}{I}_{\mathrm{1}} +\frac{−\mathrm{4}}{\mathrm{55}}=\mathrm{0}\:\:\: \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{55}} \\ $$$${current}\:{through}\:{R}_{\mathrm{1}} =\frac{\mathrm{24}}{\mathrm{55}} \\ $$$${R}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{55}} \\ $$$${R}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{55}}−\left(\frac{−\mathrm{24}}{\mathrm{55}}\right)=\frac{\mathrm{25}}{\mathrm{55}} \\ $$$${V}_{{a}} \sim{V}_{{b}} ={E}_{\mathrm{3}} −{R}_{\mathrm{3}} \left({I}_{\mathrm{1}} −{I}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{10}−\mathrm{4}×\frac{\mathrm{25}}{\mathrm{55}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{550}−\mathrm{100}}{\mathrm{55}}=\frac{\mathrm{450}}{\mathrm{55}}=\frac{\mathrm{90}}{\mathrm{11}} \\ $$$${pls}\:{check}\:{is}\:{it}\:{correct}…{if}\:{not}\:{where}\:{the}\:{wrong} \\ $$
Commented by rahul 19 last updated on 04/Jul/18
Correct! But I asked for parallel grp. method .
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jul/18
ok pls
$${ok}\:{pls} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *