Question Number 39003 by behi83417@gmail.com last updated on 01/Jul/18

Answered by MJS last updated on 01/Jul/18
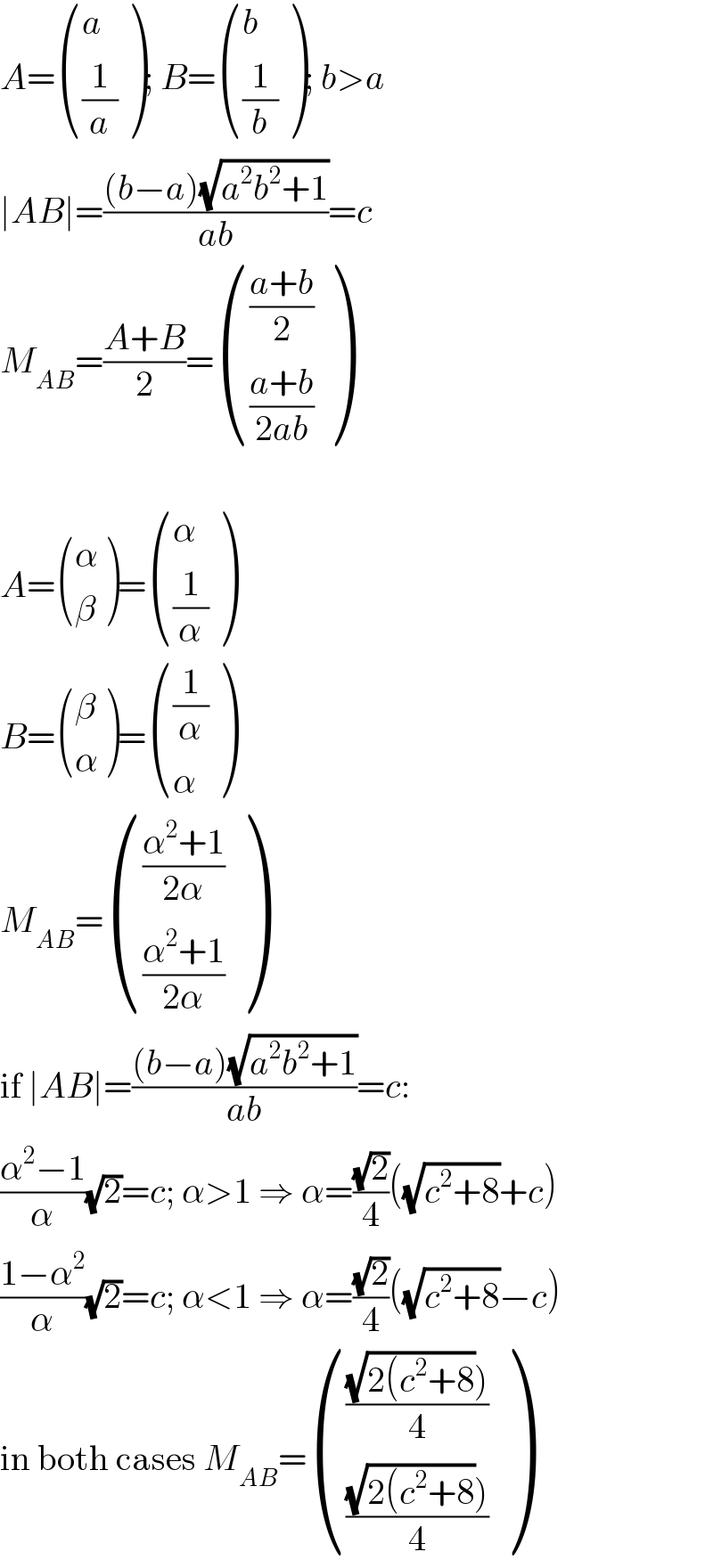
$${A}=\begin{pmatrix}{{a}}\\{\frac{\mathrm{1}}{{a}}}\end{pmatrix};\:{B}=\begin{pmatrix}{{b}}\\{\frac{\mathrm{1}}{{b}}}\end{pmatrix};\:{b}>{a} \\ $$$$\mid{AB}\mid=\frac{\left({b}−{a}\right)\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1}}}{{ab}}={c} \\ $$$${M}_{{AB}} =\frac{{A}+{B}}{\mathrm{2}}=\begin{pmatrix}{\frac{{a}+{b}}{\mathrm{2}}}\\{\frac{{a}+{b}}{\mathrm{2}{ab}}}\end{pmatrix} \\ $$$$ \\ $$$${A}=\begin{pmatrix}{\alpha}\\{\beta}\end{pmatrix}=\begin{pmatrix}{\alpha}\\{\frac{\mathrm{1}}{\alpha}}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{\beta}\\{\alpha}\end{pmatrix}=\begin{pmatrix}{\frac{\mathrm{1}}{\alpha}}\\{\alpha}\end{pmatrix} \\ $$$${M}_{{AB}} =\begin{pmatrix}{\frac{\alpha^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\alpha}}\\{\frac{\alpha^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\alpha}}\end{pmatrix} \\ $$$$\mathrm{if}\:\mid{AB}\mid=\frac{\left({b}−{a}\right)\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1}}}{{ab}}={c}: \\ $$$$\frac{\alpha^{\mathrm{2}} −\mathrm{1}}{\alpha}\sqrt{\mathrm{2}}={c};\:\alpha>\mathrm{1}\:\Rightarrow\:\alpha=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\sqrt{{c}^{\mathrm{2}} +\mathrm{8}}+{c}\right) \\ $$$$\frac{\mathrm{1}−\alpha^{\mathrm{2}} }{\alpha}\sqrt{\mathrm{2}}={c};\:\alpha<\mathrm{1}\:\Rightarrow\:\alpha=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\sqrt{{c}^{\mathrm{2}} +\mathrm{8}}−{c}\right) \\ $$$$\mathrm{in}\:\mathrm{both}\:\mathrm{cases}\:{M}_{{AB}} =\begin{pmatrix}{\frac{\left.\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +\mathrm{8}\right.}\right)}{\mathrm{4}}}\\{\frac{\left.\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +\mathrm{8}\right.}\right)}{\mathrm{4}}}\end{pmatrix} \\ $$
Commented by behi83417@gmail.com last updated on 01/Jul/18

$${dear}\:{MJS}!\:{thanks}. \\ $$$${but}\:{in}\:#\mathrm{2},{length}\:{of}\:{AB},{not}\:{constant}. \\ $$$${what}\:{about}\:{equation}\:{of}\:{locus}\:{in}#\mathrm{1\&2}? \\ $$
Answered by MrW3 last updated on 02/Jul/18
![(1) A(a,(1/a)), B(b,(1/b)) AB^2 =(a−b)^2 +((1/a)−(1/b))^2 =l^2 =const. (a−b)^2 +(((a−b)^2 )/(a^2 b^2 ))=l^2 (a−b)^2 [1+(1/(a^2 b^2 ))]=l^2 ⇒ [(a+b)^2 −4ab][1+(1/(a^2 b^2 ))]=l^2 ...(i) M(x,y) =midpoint of AB x=((a+b)/2) ⇒a+b=2x ...(ii) y=(((1/a)+(1/b))/2)=((a+b)/(2ab)) ⇒ab=(x/y) ...(iii) (ii) & (iii) into (i): [(2x)^2 −4(x/y)][1+(1/(((x/y))^2 ))]=l^2 [4x^2 −4(x/y)][1+(y^2 /x^2 )]=l^2 ⇒4(xy−1)(x^2 +y^2 )−xyl^2 =0 see graph with l=6:](https://www.tinkutara.com/question/Q39042.png)
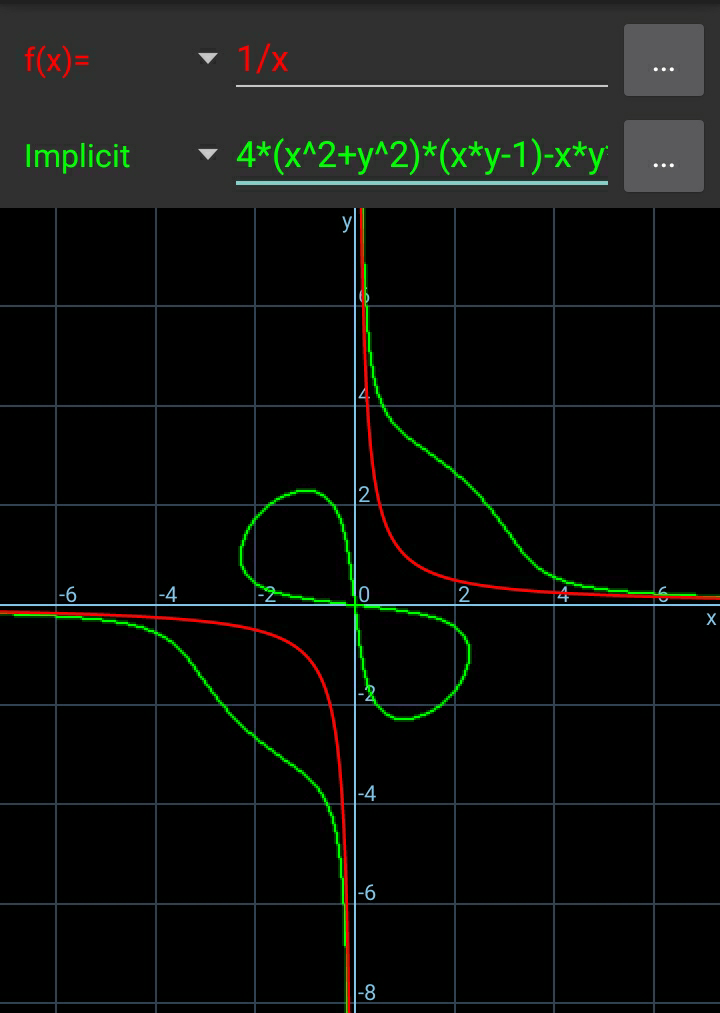
$$\left(\mathrm{1}\right) \\ $$$${A}\left({a},\frac{\mathrm{1}}{{a}}\right),\:{B}\left({b},\frac{\mathrm{1}}{{b}}\right) \\ $$$${AB}^{\mathrm{2}} =\left({a}−{b}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{b}}\right)^{\mathrm{2}} ={l}^{\mathrm{2}} ={const}. \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} +\frac{\left({a}−{b}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }={l}^{\mathrm{2}} \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} \left[\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right]={l}^{\mathrm{2}} \\ $$$$\Rightarrow\:\left[\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{ab}\right]\left[\mathrm{1}+\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right]={l}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${M}\left({x},{y}\right)\:={midpoint}\:{of}\:{AB} \\ $$$${x}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\Rightarrow{a}+{b}=\mathrm{2}{x}\:\:\:\:…\left({ii}\right) \\ $$$${y}=\frac{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}}{\mathrm{2}}=\frac{{a}+{b}}{\mathrm{2}{ab}} \\ $$$$\Rightarrow{ab}=\frac{{x}}{{y}}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({ii}\right)\:\&\:\left({iii}\right)\:{into}\:\left({i}\right): \\ $$$$\left[\left(\mathrm{2}{x}\right)^{\mathrm{2}} −\mathrm{4}\frac{{x}}{{y}}\right]\left[\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} }\right]={l}^{\mathrm{2}} \\ $$$$\left[\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}\frac{{x}}{{y}}\right]\left[\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right]={l}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}\left({xy}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−{xyl}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${see}\:{graph}\:{with}\:{l}=\mathrm{6}: \\ $$
Commented by MrW3 last updated on 02/Jul/18
Commented by MrW3 last updated on 02/Jul/18
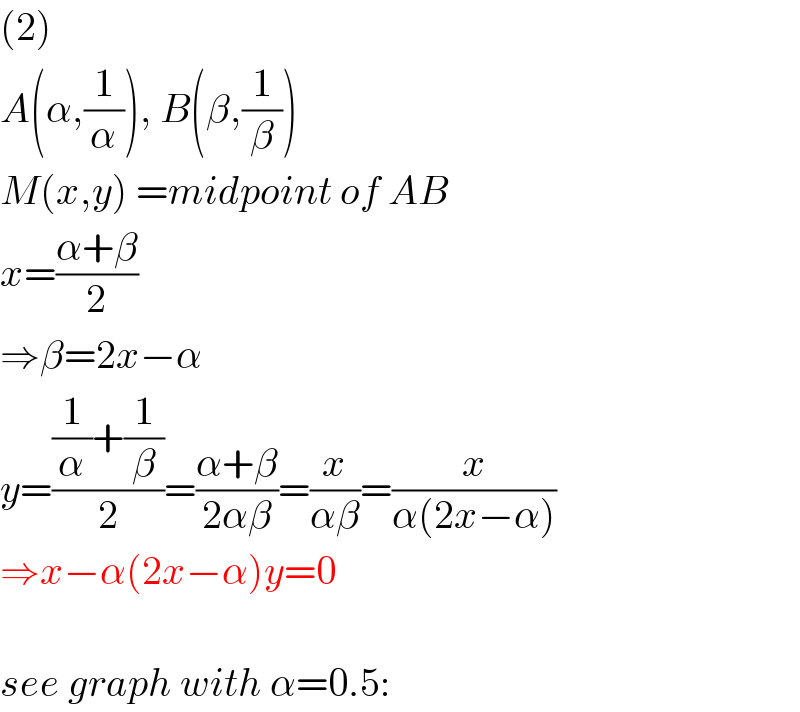
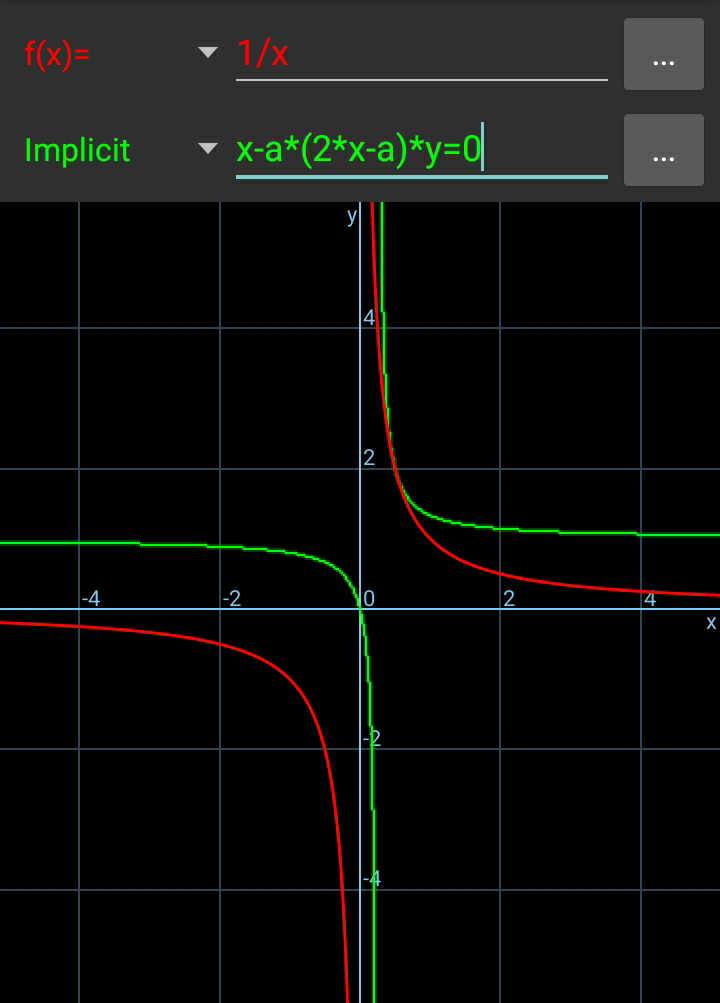
$$\left(\mathrm{2}\right) \\ $$$${A}\left(\alpha,\frac{\mathrm{1}}{\alpha}\right),\:{B}\left(\beta,\frac{\mathrm{1}}{\beta}\right) \\ $$$${M}\left({x},{y}\right)\:={midpoint}\:{of}\:{AB} \\ $$$${x}=\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$\Rightarrow\beta=\mathrm{2}{x}−\alpha \\ $$$${y}=\frac{\frac{\mathrm{1}}{\alpha}+\frac{\mathrm{1}}{\beta}}{\mathrm{2}}=\frac{\alpha+\beta}{\mathrm{2}\alpha\beta}=\frac{{x}}{\alpha\beta}=\frac{{x}}{\alpha\left(\mathrm{2}{x}−\alpha\right)} \\ $$$$\Rightarrow{x}−\alpha\left(\mathrm{2}{x}−\alpha\right){y}=\mathrm{0} \\ $$$$ \\ $$$${see}\:{graph}\:{with}\:\alpha=\mathrm{0}.\mathrm{5}: \\ $$
Commented by MrW3 last updated on 02/Jul/18
Commented by behi83417@gmail.com last updated on 02/Jul/18

$${dear}\:{master}!{thank}\:{you}\:{very}\:{much}. \\ $$$${alwyes}\:{the}\:{best}.{your}\:{answers}\:{are} \\ $$$${the}\:{finishing}\:{bullets}\:{to}\:{the}\:{heart}\:{of} \\ $$$${questions}.{being}\:{you}\:{in}\:{this}\:{forum}\: \\ $$$${encouraged}\:{me}.{do}\:{not}\:{be}\:{far}\:{from}\:{us} \\ $$$${any}\:{more}.{god}\:{bless}\:\:{you}. \\ $$
Commented by MrW3 last updated on 02/Jul/18
$${Thank}\:{you}\:{too}!\:{I}'{ll}\:{try}\:{not}\:{to}\:{go}\:{too}\:{far} \\ $$$$\left.{away}\:{from}\:{this}\:{forum}\::\right) \\ $$
