Question Number 39089 by ajfour last updated on 02/Jul/18
Commented by ajfour last updated on 02/Jul/18
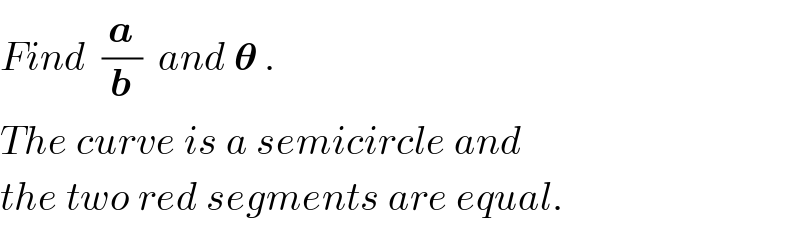
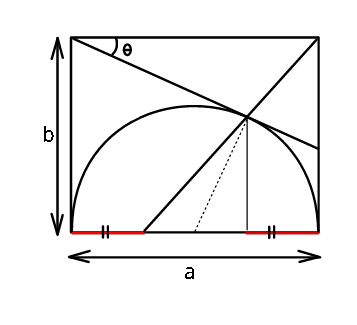
$${Find}\:\:\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}}\:\:{and}\:\boldsymbol{\theta}\:. \\ $$$${The}\:{curve}\:{is}\:{a}\:{semicircle}\:{and} \\ $$$${the}\:{two}\:{red}\:{segments}\:{are}\:{equal}. \\ $$
Answered by MJS last updated on 02/Jul/18
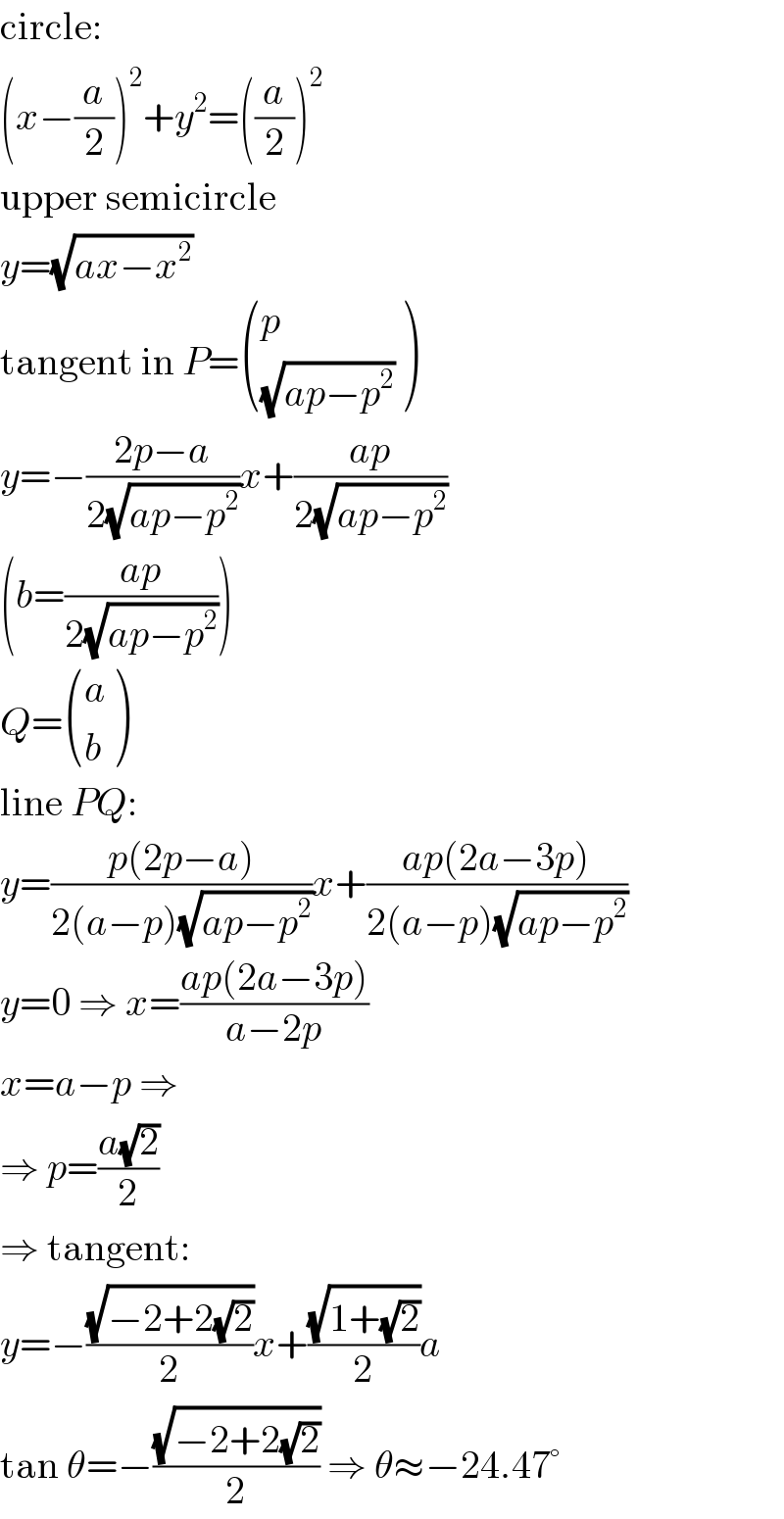
$$\mathrm{circle}: \\ $$$$\left({x}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{upper}\:\mathrm{semicircle} \\ $$$${y}=\sqrt{{ax}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{tangent}\:\mathrm{in}\:{P}=\begin{pmatrix}{{p}}\\{\sqrt{{ap}−{p}^{\mathrm{2}} }}\end{pmatrix} \\ $$$${y}=−\frac{\mathrm{2}{p}−{a}}{\mathrm{2}\sqrt{{ap}−{p}^{\mathrm{2}} }}{x}+\frac{{ap}}{\mathrm{2}\sqrt{{ap}−{p}^{\mathrm{2}} }} \\ $$$$\left({b}=\frac{{ap}}{\mathrm{2}\sqrt{{ap}−{p}^{\mathrm{2}} }}\right) \\ $$$${Q}=\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix} \\ $$$$\mathrm{line}\:{PQ}: \\ $$$${y}=\frac{{p}\left(\mathrm{2}{p}−{a}\right)}{\mathrm{2}\left({a}−{p}\right)\sqrt{{ap}−{p}^{\mathrm{2}} }}{x}+\frac{{ap}\left(\mathrm{2}{a}−\mathrm{3}{p}\right)}{\mathrm{2}\left({a}−{p}\right)\sqrt{{ap}−{p}^{\mathrm{2}} }} \\ $$$${y}=\mathrm{0}\:\Rightarrow\:{x}=\frac{{ap}\left(\mathrm{2}{a}−\mathrm{3}{p}\right)}{{a}−\mathrm{2}{p}} \\ $$$${x}={a}−{p}\:\Rightarrow \\ $$$$\Rightarrow\:{p}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{tangent}: \\ $$$${y}=−\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}}{x}+\frac{\sqrt{\mathrm{1}+\sqrt{\mathrm{2}}}}{\mathrm{2}}{a} \\ $$$$\mathrm{tan}\:\theta=−\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}}\:\Rightarrow\:\theta\approx−\mathrm{24}.\mathrm{47}° \\ $$
Commented by ajfour last updated on 02/Jul/18
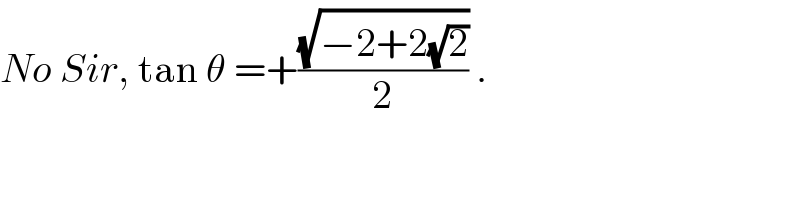
$${No}\:{Sir},\:\mathrm{tan}\:\theta\:=+\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}}\:. \\ $$
Commented by MJS last updated on 02/Jul/18

$$\mathrm{yes}\:\mathrm{of}\:\mathrm{course},\:\mathrm{if}\:\mathrm{you}\:\mathrm{measure}\:\theta\:\mathrm{as}\:\mathrm{a}\:\mathrm{positive} \\ $$$$\mathrm{angle}.\:\mathrm{my}\:\mathrm{solution}\:\mathrm{comes}\:\mathrm{from}\:\mathrm{the}\:\mathrm{tangent} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{decreasing}… \\ $$
Commented by ajfour last updated on 02/Jul/18
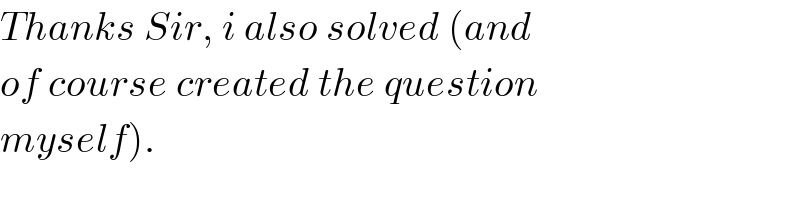
$${Thanks}\:{Sir},\:{i}\:{also}\:{solved}\:\left({and}\right. \\ $$$${of}\:{course}\:{created}\:{the}\:{question} \\ $$$$\left.{myself}\right). \\ $$
Commented by MJS last updated on 02/Jul/18

$$\mathrm{I}\:\mathrm{like}\:\mathrm{your}\:\mathrm{geometric}\:\mathrm{questions}\:\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{very} \\ $$$$\mathrm{interesting}\:\mathrm{how}\:\mathrm{different}\:\mathrm{people}\:\mathrm{differently} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{same}\:\mathrm{problems} \\ $$
Answered by ajfour last updated on 02/Jul/18
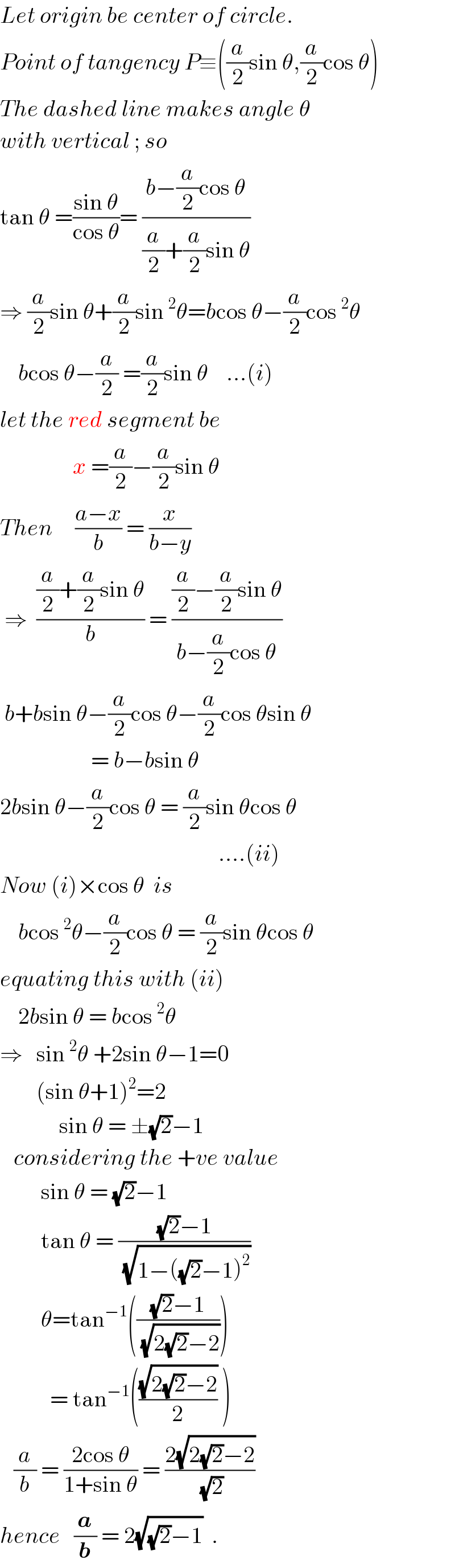
$${Let}\:{origin}\:{be}\:{center}\:{of}\:{circle}. \\ $$$${Point}\:{of}\:{tangency}\:{P}\equiv\left(\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta,\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta\right) \\ $$$${The}\:{dashed}\:{line}\:{makes}\:{angle}\:\theta \\ $$$${with}\:{vertical}\:;\:{so} \\ $$$$\mathrm{tan}\:\theta\:=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}=\:\frac{{b}−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta}{\frac{{a}}{\mathrm{2}}+\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\:\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta+\frac{{a}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \theta={b}\mathrm{cos}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:{b}\mathrm{cos}\:\theta−\frac{{a}}{\mathrm{2}}\:=\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta\:\:\:\:…\left({i}\right) \\ $$$${let}\:{the}\:{red}\:{segment}\:{be} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:=\frac{{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$${Then}\:\:\:\:\:\frac{{a}−{x}}{{b}}\:=\:\frac{{x}}{{b}−{y}} \\ $$$$\:\Rightarrow\:\:\frac{\frac{{a}}{\mathrm{2}}+\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta}{{b}}\:=\:\frac{\frac{{a}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta}{{b}−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta} \\ $$$$\:{b}+{b}\mathrm{sin}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{b}−{b}\mathrm{sin}\:\theta \\ $$$$\mathrm{2}{b}\mathrm{sin}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta\:=\:\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${Now}\:\left({i}\right)×\mathrm{cos}\:\theta\:\:{is} \\ $$$$\:\:\:\:{b}\mathrm{cos}\:^{\mathrm{2}} \theta−\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\theta\:=\:\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${equating}\:{this}\:{with}\:\left({ii}\right) \\ $$$$\:\:\:\:\mathrm{2}{b}\mathrm{sin}\:\theta\:=\:{b}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:^{\mathrm{2}} \theta\:+\mathrm{2sin}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{sin}\:\theta+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\theta\:=\:\pm\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\:\:\:{considering}\:{the}\:+{ve}\:{value} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\theta\:=\:\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}{\mathrm{2}}\:\right)\: \\ $$$$\:\:\:\frac{{a}}{{b}}\:=\:\frac{\mathrm{2cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}{\:\sqrt{\mathrm{2}}} \\ $$$${hence}\:\:\:\frac{\boldsymbol{{a}}}{\boldsymbol{{b}}}\:=\:\mathrm{2}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\:\:. \\ $$
