Question Number 39104 by behi83417@gmail.com last updated on 02/Jul/18

Commented by behi83417@gmail.com last updated on 02/Jul/18
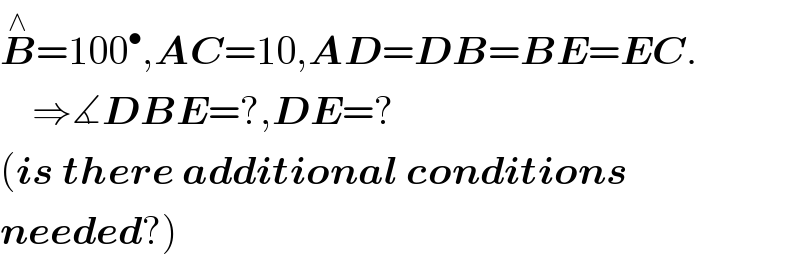
$$\overset{\wedge} {\boldsymbol{{B}}}=\mathrm{100}^{\bullet} ,\boldsymbol{{AC}}=\mathrm{10},\boldsymbol{{AD}}=\boldsymbol{{DB}}=\boldsymbol{{BE}}=\boldsymbol{{EC}}. \\ $$$$\:\:\:\:\Rightarrow\measuredangle\boldsymbol{{DBE}}=?,\boldsymbol{{DE}}=? \\ $$$$\left(\boldsymbol{{is}}\:\boldsymbol{{there}}\:\boldsymbol{{additional}}\:\boldsymbol{{conditions}}\right. \\ $$$$\left.\boldsymbol{{needed}}?\right) \\ $$
Answered by MrW3 last updated on 02/Jul/18
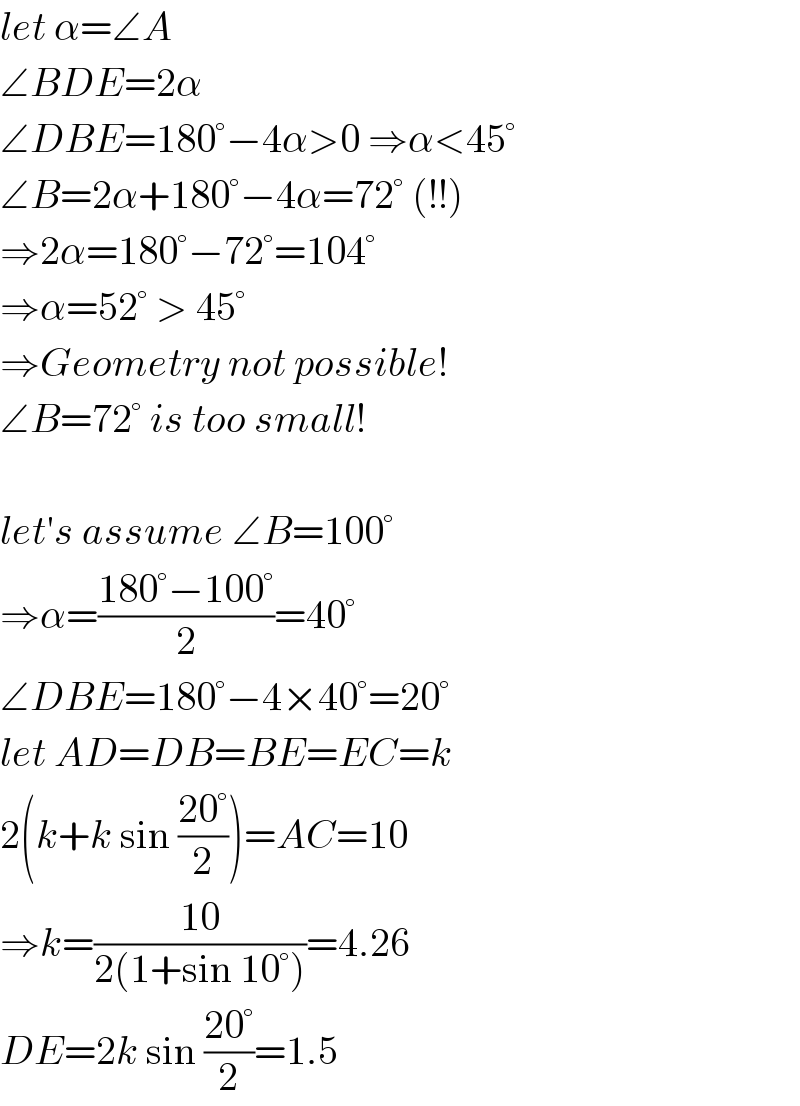
$${let}\:\alpha=\angle{A} \\ $$$$\angle{BDE}=\mathrm{2}\alpha \\ $$$$\angle{DBE}=\mathrm{180}°−\mathrm{4}\alpha>\mathrm{0}\:\Rightarrow\alpha<\mathrm{45}° \\ $$$$\angle{B}=\mathrm{2}\alpha+\mathrm{180}°−\mathrm{4}\alpha=\mathrm{72}°\:\left(!!\right) \\ $$$$\Rightarrow\mathrm{2}\alpha=\mathrm{180}°−\mathrm{72}°=\mathrm{104}° \\ $$$$\Rightarrow\alpha=\mathrm{52}°\:>\:\mathrm{45}° \\ $$$$\Rightarrow{Geometry}\:{not}\:{possible}! \\ $$$$\angle{B}=\mathrm{72}°\:{is}\:{too}\:{small}! \\ $$$$ \\ $$$${let}'{s}\:{assume}\:\angle{B}=\mathrm{100}° \\ $$$$\Rightarrow\alpha=\frac{\mathrm{180}°−\mathrm{100}°}{\mathrm{2}}=\mathrm{40}° \\ $$$$\angle{DBE}=\mathrm{180}°−\mathrm{4}×\mathrm{40}°=\mathrm{20}° \\ $$$${let}\:{AD}={DB}={BE}={EC}={k} \\ $$$$\mathrm{2}\left({k}+{k}\:\mathrm{sin}\:\frac{\mathrm{20}°}{\mathrm{2}}\right)={AC}=\mathrm{10} \\ $$$$\Rightarrow{k}=\frac{\mathrm{10}}{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{10}°\right)}=\mathrm{4}.\mathrm{26} \\ $$$${DE}=\mathrm{2}{k}\:\mathrm{sin}\:\frac{\mathrm{20}°}{\mathrm{2}}=\mathrm{1}.\mathrm{5} \\ $$
Commented by behi83417@gmail.com last updated on 02/Jul/18
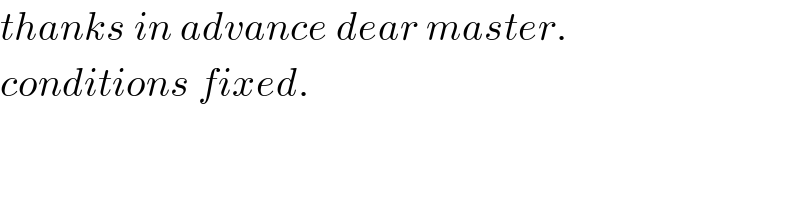
$${thanks}\:{in}\:{advance}\:{dear}\:{master}. \\ $$$${conditions}\:{fixed}. \\ $$
