Menu Close

Question-39156

Tinku Tara 0 Comments
Pin




Question Number 39156 by rahul 19 last updated on 03/Jul/18
Answered by MJS last updated on 03/Jul/18
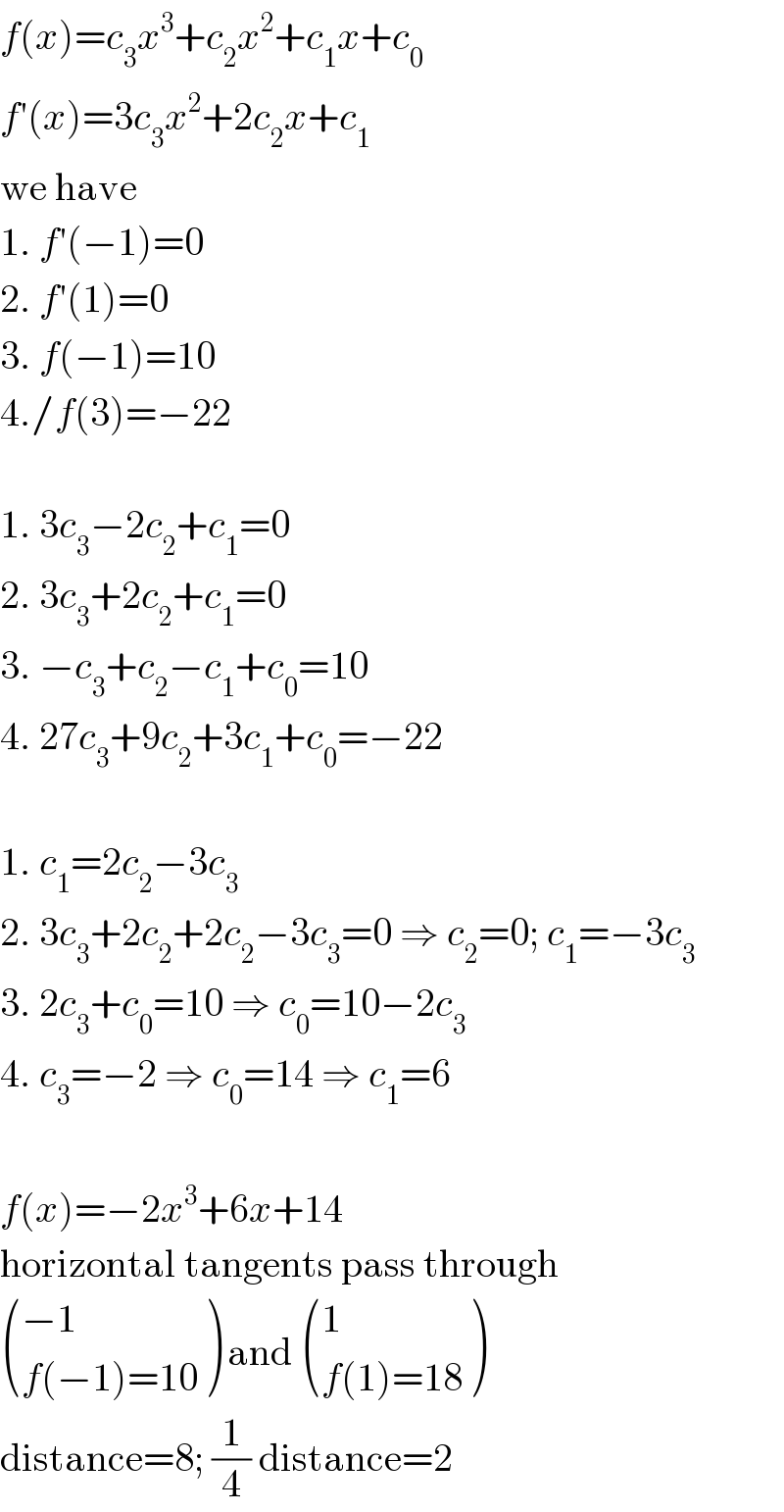
f(x)=c_3 x^3 +c_2 x^2 +c_1 x+c_0 f′(x)=3c_3 x^2 +2c_2 x+c_1 we have 1. f′(−1)=0 2. f′(1)=0 3. f(−1)=10 4./f(3)=−22 1. 3c_3 −2c_2 +c_1 =0 2. 3c_3 +2c_2 +c_1 =0 3. −c_3 +c_2 −c_1 +c_0 =10 4. 27c_3 +9c_2 +3c_1 +c_0 =−22 1. c_1 =2c_2 −3c_3 2. 3c_3 +2c_2 +2c_2 −3c_3 =0 ⇒ c_2 =0; c_1 =−3c_3 3. 2c_3 +c_0 =10 ⇒ c_0 =10−2c_3 4. c_3 =−2 ⇒ c_0 =14 ⇒ c_1 =6 f(x)=−2x^3 +6x+14 horizontal tangents pass through (((−1)),((f(−1)=10)) ) and ((1),((f(1)=18)) ) distance=8; (1/4) distance=2
$${f}\left({x}\right)={c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} \\ $$$${f}'\left({x}\right)=\mathrm{3}{c}_{\mathrm{3}} {x}^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{2}} {x}+{c}_{\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{1}.\:{f}'\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{2}.\:{f}'\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{3}.\:{f}\left(−\mathrm{1}\right)=\mathrm{10} \\ $$$$\mathrm{4}./{f}\left(\mathrm{3}\right)=−\mathrm{22} \\ $$$$ \\ $$$$\mathrm{1}.\:\mathrm{3}{c}_{\mathrm{3}} −\mathrm{2}{c}_{\mathrm{2}} +{c}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{2}.\:\mathrm{3}{c}_{\mathrm{3}} +\mathrm{2}{c}_{\mathrm{2}} +{c}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{3}.\:−{c}_{\mathrm{3}} +{c}_{\mathrm{2}} −{c}_{\mathrm{1}} +{c}_{\mathrm{0}} =\mathrm{10} \\ $$$$\mathrm{4}.\:\mathrm{27}{c}_{\mathrm{3}} +\mathrm{9}{c}_{\mathrm{2}} +\mathrm{3}{c}_{\mathrm{1}} +{c}_{\mathrm{0}} =−\mathrm{22} \\ $$$$ \\ $$$$\mathrm{1}.\:{c}_{\mathrm{1}} =\mathrm{2}{c}_{\mathrm{2}} −\mathrm{3}{c}_{\mathrm{3}} \\ $$$$\mathrm{2}.\:\mathrm{3}{c}_{\mathrm{3}} +\mathrm{2}{c}_{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{2}} −\mathrm{3}{c}_{\mathrm{3}} =\mathrm{0}\:\Rightarrow\:{c}_{\mathrm{2}} =\mathrm{0};\:{c}_{\mathrm{1}} =−\mathrm{3}{c}_{\mathrm{3}} \\ $$$$\mathrm{3}.\:\mathrm{2}{c}_{\mathrm{3}} +{c}_{\mathrm{0}} =\mathrm{10}\:\Rightarrow\:{c}_{\mathrm{0}} =\mathrm{10}−\mathrm{2}{c}_{\mathrm{3}} \\ $$$$\mathrm{4}.\:{c}_{\mathrm{3}} =−\mathrm{2}\:\Rightarrow\:{c}_{\mathrm{0}} =\mathrm{14}\:\Rightarrow\:{c}_{\mathrm{1}} =\mathrm{6} \\ $$$$ \\ $$$${f}\left({x}\right)=−\mathrm{2}{x}^{\mathrm{3}} +\mathrm{6}{x}+\mathrm{14} \\ $$$$\mathrm{horizontal}\:\mathrm{tangents}\:\mathrm{pass}\:\mathrm{through} \\ $$$$\begin{pmatrix}{−\mathrm{1}}\\{{f}\left(−\mathrm{1}\right)=\mathrm{10}}\end{pmatrix}\:\mathrm{and}\:\begin{pmatrix}{\mathrm{1}}\\{{f}\left(\mathrm{1}\right)=\mathrm{18}}\end{pmatrix} \\ $$$$\mathrm{distance}=\mathrm{8};\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{distance}=\mathrm{2} \\ $$
Commented by rahul 19 last updated on 03/Jul/18
Thank you sir :)
$$\left.\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}\::\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *