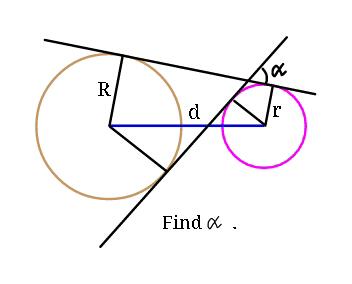
Question Number 39175 by ajfour last updated on 03/Jul/18
Answered by MJS last updated on 03/Jul/18
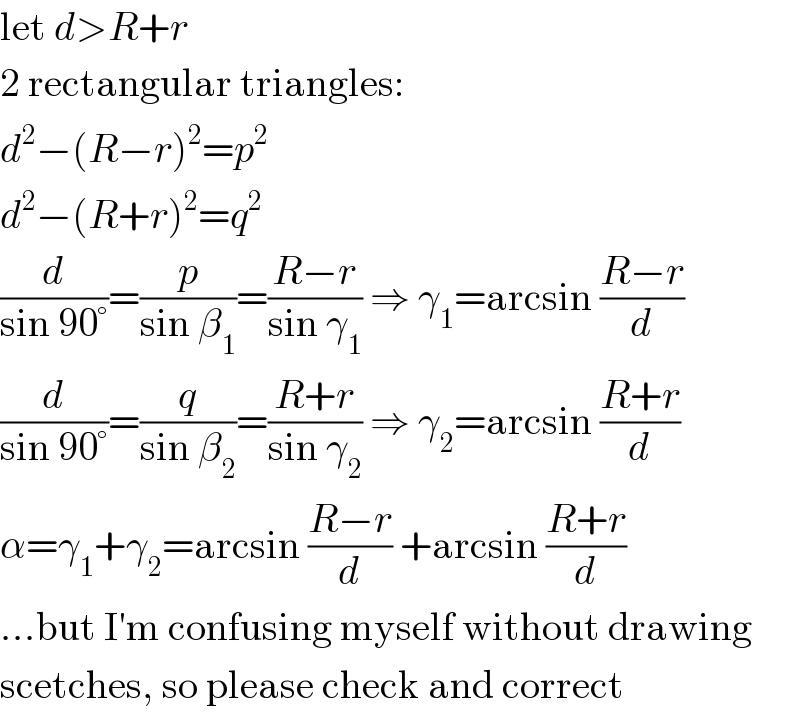
$$\mathrm{let}\:{d}>{R}+{r} \\ $$$$\mathrm{2}\:\mathrm{rectangular}\:\mathrm{triangles}: \\ $$$${d}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} −\left({R}+{r}\right)^{\mathrm{2}} ={q}^{\mathrm{2}} \\ $$$$\frac{{d}}{\mathrm{sin}\:\mathrm{90}°}=\frac{{p}}{\mathrm{sin}\:\beta_{\mathrm{1}} }=\frac{{R}−{r}}{\mathrm{sin}\:\gamma_{\mathrm{1}} }\:\Rightarrow\:\gamma_{\mathrm{1}} =\mathrm{arcsin}\:\frac{{R}−{r}}{{d}} \\ $$$$\frac{{d}}{\mathrm{sin}\:\mathrm{90}°}=\frac{{q}}{\mathrm{sin}\:\beta_{\mathrm{2}} }=\frac{{R}+{r}}{\mathrm{sin}\:\gamma_{\mathrm{2}} }\:\Rightarrow\:\gamma_{\mathrm{2}} =\mathrm{arcsin}\:\frac{{R}+{r}}{{d}} \\ $$$$\alpha=\gamma_{\mathrm{1}} +\gamma_{\mathrm{2}} =\mathrm{arcsin}\:\frac{{R}−{r}}{{d}}\:+\mathrm{arcsin}\:\frac{{R}+{r}}{{d}} \\ $$$$…\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{confusing}\:\mathrm{myself}\:\mathrm{without}\:\mathrm{drawing} \\ $$$$\mathrm{scetches},\:\mathrm{so}\:\mathrm{please}\:\mathrm{check}\:\mathrm{and}\:\mathrm{correct} \\ $$
Commented by ajfour last updated on 04/Jul/18
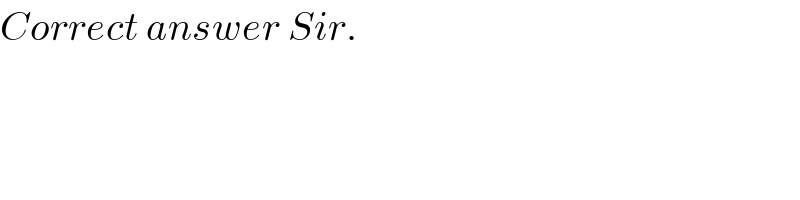
$${Correct}\:{answer}\:{Sir}. \\ $$
Commented by MJS last updated on 04/Jul/18

$$\mathrm{thank}\:\mathrm{you} \\ $$
