Menu Close

Question-39177

Tinku Tara 0 Comments
Pin




Question Number 39177 by ajfour last updated on 03/Jul/18
Commented by ajfour last updated on 03/Jul/18
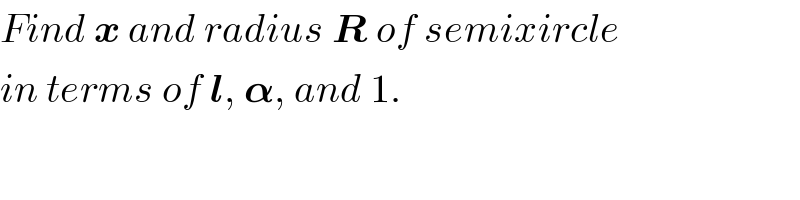
Find x and radius R of semixircle in terms of l, 𝛂, and 1.
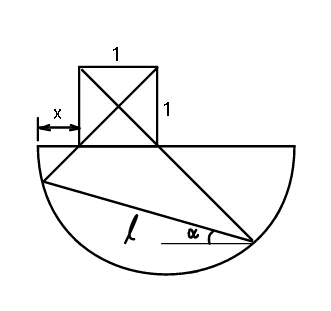
$${Find}\:\boldsymbol{{x}}\:{and}\:{radius}\:\boldsymbol{{R}}\:{of}\:{semixircle} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{l}},\:\boldsymbol{\alpha},\:{and}\:\mathrm{1}. \\ $$
Commented by MJS last updated on 03/Jul/18
new idea start with the center of the square and the triangle “sitting” on the x−axis now it′s possible to choose l and α and then construct/calculate the rest first the circle through the vericles and with its center on the x−axis, then find x (which I′d like to call z instead)
$$\mathrm{new}\:\mathrm{idea} \\ $$$$\mathrm{start}\:\mathrm{with}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:“\mathrm{sitting}''\:\mathrm{on}\:\mathrm{the}\:{x}−\mathrm{axis} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{choose}\:{l}\:\mathrm{and}\:\alpha\:\mathrm{and}\:\mathrm{then} \\ $$$$\mathrm{construct}/\mathrm{calculate}\:\mathrm{the}\:\mathrm{rest} \\ $$$$\mathrm{first}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{through}\:\mathrm{the}\:\mathrm{vericles}\:\mathrm{and}\:\mathrm{with} \\ $$$$\mathrm{its}\:\mathrm{center}\:\mathrm{on}\:\mathrm{the}\:{x}−\mathrm{axis},\:\mathrm{then}\:\mathrm{find}\:{x}\:\left(\mathrm{which}\right. \\ $$$$\left.\mathrm{I}'\mathrm{d}\:\mathrm{like}\:\mathrm{to}\:\mathrm{call}\:{z}\:\mathrm{instead}\right) \\ $$
Answered by MrW3 last updated on 04/Jul/18
Commented by MrW3 last updated on 04/Jul/18
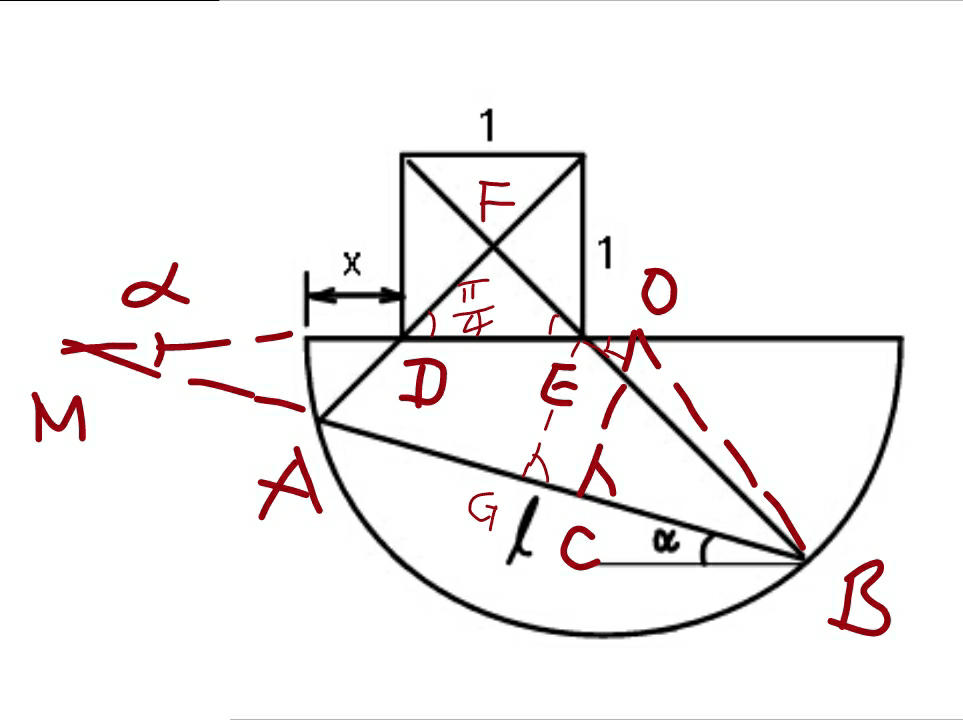
let a=side length of square=1 C=midpoint of AB ∠ABF=(π/4)−α AD=AF−DF=l sin ((π/4)−α)−(a/( (√2))) =((l (cos α−sin α)−a)/( (√2))) ((MA)/(sin (π/4)))=((AD)/(sin α)) ⇒MA=((AD)/( (√2) sin α))=((l (cos α−sin α)−a)/(2 sin α)) OC=MC tan α=(MA+(l/2)) tan α =[((l (cos α−sin α)−a)/(2 sin α))+(l/2)]tan α =((l cos α−a)/(2 cos α))=(l/2)−(a/(2 cos α)) R=OB=(√(OC^2 +CB^2 )) =(√(((l/2)−(a/(2 cos α)))^2 +((l/2))^2 )) =(√((l^2 /2)−((la)/(2 cos α))+(a^2 /(4 cos^2 α)))) ⇒R=((√(a^2 +2lcos α(l cos α−a)))/(2 cos α)) EB=FB−FE=l cos ((π/4)−α)−(a/( (√2))) =((l (cos α+sin α)−a)/( (√2))) ((GB)/(EB))=((FB)/(AB))=((l (cos α+sin α))/( (√2) l))=((cos α+sin α)/( (√2))) ⇒GB=((cos α+sin α)/( (√2)))×((l (cos α+sin α)−a)/( (√2))) =((l (1+sin 2α)−a(cos α+sin α))/2) EO=((GC)/(cos α))=(GB−CB)(1/(cos α)) =[((l (1+sin 2α)−a(cos α+sin α))/2)−(l/2)](1/(cos α)) =((l sin 2α−a(cos α+sin α))/(2 cos α)) =l sin α−(a/2)(1+tan α) x=R−EO−DE =R−l sin α+(a/2)(1+tan α)−a ⇒x=R−l sin α−(a/2)(1−tan α)
$${let}\:{a}={side}\:{length}\:{of}\:{square}=\mathrm{1} \\ $$$${C}={midpoint}\:{of}\:{AB} \\ $$$$\angle{ABF}=\frac{\pi}{\mathrm{4}}−\alpha \\ $$$$ \\ $$$${AD}={AF}−{DF}={l}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)−\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{{l}\:\left(\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\right)−{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$\frac{{MA}}{\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}=\frac{{AD}}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow{MA}=\frac{{AD}}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\alpha}=\frac{{l}\:\left(\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\right)−{a}}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$$ \\ $$$${OC}={MC}\:\mathrm{tan}\:\alpha=\left({MA}+\frac{{l}}{\mathrm{2}}\right)\:\mathrm{tan}\:\alpha \\ $$$$=\left[\frac{{l}\:\left(\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\right)−{a}}{\mathrm{2}\:\mathrm{sin}\:\alpha}+\frac{{l}}{\mathrm{2}}\right]\mathrm{tan}\:\alpha \\ $$$$=\frac{{l}\:\mathrm{cos}\:\alpha−{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha}=\frac{{l}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$${R}={OB}=\sqrt{{OC}^{\mathrm{2}} +{CB}^{\mathrm{2}} } \\ $$$$=\sqrt{\left(\frac{{l}}{\mathrm{2}}−\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha}\right)^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\frac{{l}^{\mathrm{2}} }{\mathrm{2}}−\frac{{la}}{\mathrm{2}\:\mathrm{cos}\:\alpha}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\alpha}} \\ $$$$\Rightarrow{R}=\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{l}\mathrm{cos}\:\alpha\left({l}\:\mathrm{cos}\:\alpha−{a}\right)}}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$${EB}={FB}−{FE}={l}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)−\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{{l}\:\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)−{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{GB}}{{EB}}=\frac{{FB}}{{AB}}=\frac{{l}\:\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)}{\:\sqrt{\mathrm{2}}\:{l}}=\frac{\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{GB}=\frac{\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{2}}}×\frac{{l}\:\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)−{a}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{{l}\:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}\alpha\right)−{a}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)}{\mathrm{2}} \\ $$$${EO}=\frac{{GC}}{\mathrm{cos}\:\alpha}=\left({GB}−{CB}\right)\frac{\mathrm{1}}{\mathrm{cos}\:\alpha} \\ $$$$=\left[\frac{{l}\:\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}\alpha\right)−{a}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)}{\mathrm{2}}−\frac{{l}}{\mathrm{2}}\right]\frac{\mathrm{1}}{\mathrm{cos}\:\alpha} \\ $$$$=\frac{{l}\:\mathrm{sin}\:\mathrm{2}\alpha−{a}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$={l}\:\mathrm{sin}\:\alpha−\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right) \\ $$$$ \\ $$$${x}={R}−{EO}−{DE} \\ $$$$={R}−{l}\:\mathrm{sin}\:\alpha+\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)−{a} \\ $$$$\Rightarrow{x}={R}−{l}\:\mathrm{sin}\:\alpha−\frac{{a}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}\:\alpha\right) \\ $$
Commented by ajfour last updated on 04/Jul/18
Overwhelming, Thank you Sir.
$${Overwhelming},\:{Thank}\:{you}\:{Sir}. \\ $$
Answered by MJS last updated on 04/Jul/18
center of square C= ((0),((1/2)) ) A on y=(1/2)+x; B on y=(1/2)−x A= ((a),(((1/2)+a)) ) B= ((b),(((1/2)−b)) ) line l: y=d−xtan α ∣AB∣^2 =l^2 =2a^2 +2b^2 ⇒ a=−((√(2l^2 −4b^2 ))/2) A on l: (1/2)+a=d−atan α ⇒ d=(1/2)+a(1+tan α) d=(1/2)−((√(2l^2 −4b^2 ))/2)(1+tan α) B on l: (1/2)−b=d−btan α ⇒ b=((1−2d)/(2(1−tan α))) b=((l(1+tan α))/(2(√(1+tan^2 α))))=(l/2)(sin α +cos α) ⇒ ⇒ a=−((l(1−tan α))/(2(√(1+tan^2 α))))=(l/2)(sin α −cos α) A= ((((l/2)(sin α −cos α))),(((1/2)+(l/2)(sin α −cos α))) ) B= ((((l/2)(sin α +cos α))),(((1/2)−(l/2)(sin α +cos α))) ) center of circle: M= ((m),(0) ) (x−m)^2 +y^2 =r^2 A on circle, B on circle ⇒ ⇒ m=((l/( (√(1+tan^2 α))))−(1/2))tan α=lsin α −(1/2)tan α r=(1/2)(√(2l^2 +1+tan^2 α−2l(√(1+tan^2 α))))= =(√((l^2 /2)−(l/(2cos α))+(1/(4cos^2 α)))) z=r−m−(1/2)
$$\mathrm{center}\:\mathrm{of}\:\mathrm{square} \\ $$$${C}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$$${A}\:\mathrm{on}\:{y}=\frac{\mathrm{1}}{\mathrm{2}}+{x};\:{B}\:\mathrm{on}\:{y}=\frac{\mathrm{1}}{\mathrm{2}}−{x} \\ $$$${A}=\begin{pmatrix}{{a}}\\{\frac{\mathrm{1}}{\mathrm{2}}+{a}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{{b}}\\{\frac{\mathrm{1}}{\mathrm{2}}−{b}}\end{pmatrix} \\ $$$$\mathrm{line}\:{l}:\:{y}={d}−{x}\mathrm{tan}\:\alpha \\ $$$$ \\ $$$$\mid{AB}\mid^{\mathrm{2}} ={l}^{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} \:\Rightarrow\:{a}=−\frac{\sqrt{\mathrm{2}{l}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${A}\:\mathrm{on}\:{l}:\:\frac{\mathrm{1}}{\mathrm{2}}+{a}={d}−{a}\mathrm{tan}\:\alpha\:\Rightarrow\:{d}=\frac{\mathrm{1}}{\mathrm{2}}+{a}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right) \\ $$$$\:\:\:\:\:{d}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}{l}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} }}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right) \\ $$$${B}\:\mathrm{on}\:{l}:\:\frac{\mathrm{1}}{\mathrm{2}}−{b}={d}−{b}\mathrm{tan}\:\alpha\:\Rightarrow\:{b}=\frac{\mathrm{1}−\mathrm{2}{d}}{\mathrm{2}\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)} \\ $$$$\:\:\:\:\:{b}=\frac{{l}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}=\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:+\mathrm{cos}\:\alpha\right)\:\Rightarrow \\ $$$$\:\:\:\:\:\Rightarrow\:{a}=−\frac{{l}\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}=\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:−\mathrm{cos}\:\alpha\right) \\ $$$${A}=\begin{pmatrix}{\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:−\mathrm{cos}\:\alpha\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:−\mathrm{cos}\:\alpha\right)}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:+\mathrm{cos}\:\alpha\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{l}}{\mathrm{2}}\left(\mathrm{sin}\:\alpha\:+\mathrm{cos}\:\alpha\right)}\end{pmatrix} \\ $$$$ \\ $$$$\mathrm{center}\:\mathrm{of}\:\mathrm{circle}:\:{M}=\begin{pmatrix}{{m}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\left({x}−{m}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${A}\:\mathrm{on}\:\mathrm{circle},\:{B}\:\mathrm{on}\:\mathrm{circle}\:\Rightarrow \\ $$$$\Rightarrow\:{m}=\left(\frac{{l}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{tan}\:\alpha={l}\mathrm{sin}\:\alpha\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\alpha \\ $$$$\:\:\:\:\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{l}^{\mathrm{2}} +\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha−\mathrm{2}{l}\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{{l}^{\mathrm{2}} }{\mathrm{2}}−\frac{{l}}{\mathrm{2cos}\:\alpha}+\frac{\mathrm{1}}{\mathrm{4cos}^{\mathrm{2}} \:\alpha}} \\ $$$${z}={r}−{m}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 04/Jul/18
Thank you Sir. pure coordinate method !
$${Thank}\:{you}\:{Sir}.\:{pure}\:{coordinate} \\ $$$${method}\:! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *