Question Number 39349 by ajfour last updated on 05/Jul/18

Commented by MrW3 last updated on 08/Jul/18
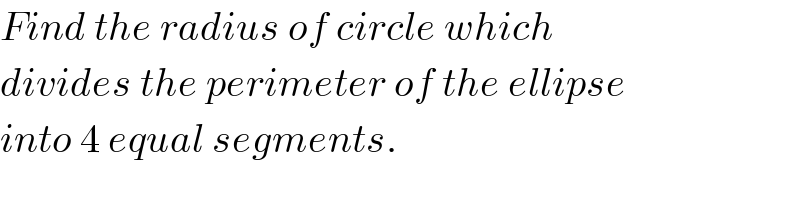
$${Find}\:{the}\:{radius}\:{of}\:{circle}\:{which} \\ $$$${divides}\:{the}\:{perimeter}\:{of}\:{the}\:{ellipse} \\ $$$${into}\:\mathrm{4}\:{equal}\:{segments}. \\ $$
Answered by MrW3 last updated on 05/Jul/18
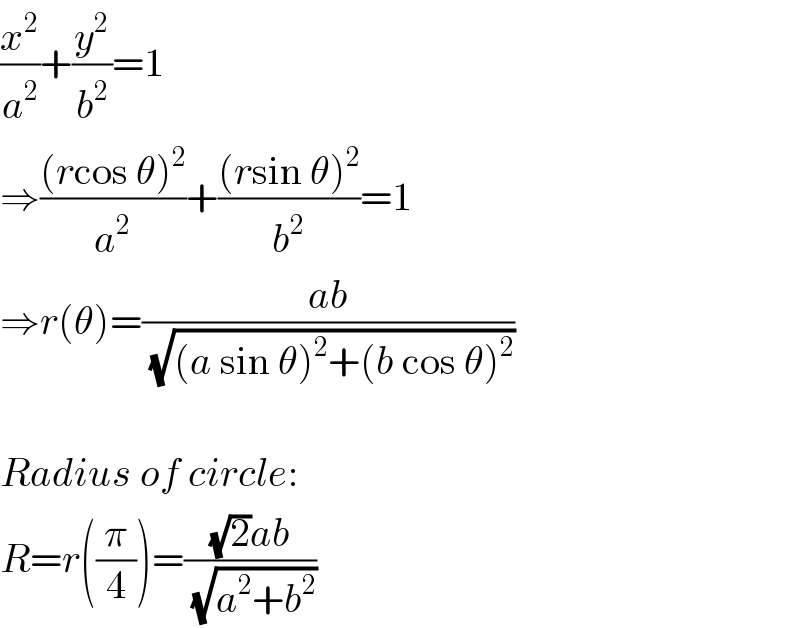
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\frac{\left({r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}\left(\theta\right)=\frac{{ab}}{\:\sqrt{\left({a}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left({b}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$${Radius}\:{of}\:{circle}: \\ $$$${R}={r}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\sqrt{\mathrm{2}}{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$
Commented by ajfour last updated on 05/Jul/18

$${Thank}\:{you}\:{Sir}! \\ $$
