Question Number 39371 by ajfour last updated on 05/Jul/18
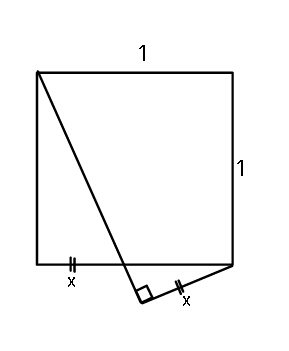
Commented by ajfour last updated on 05/Jul/18
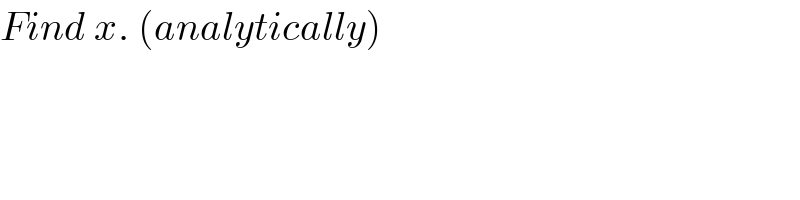
$${Find}\:{x}.\:\left({analytically}\right) \\ $$
Answered by MJS last updated on 06/Jul/18
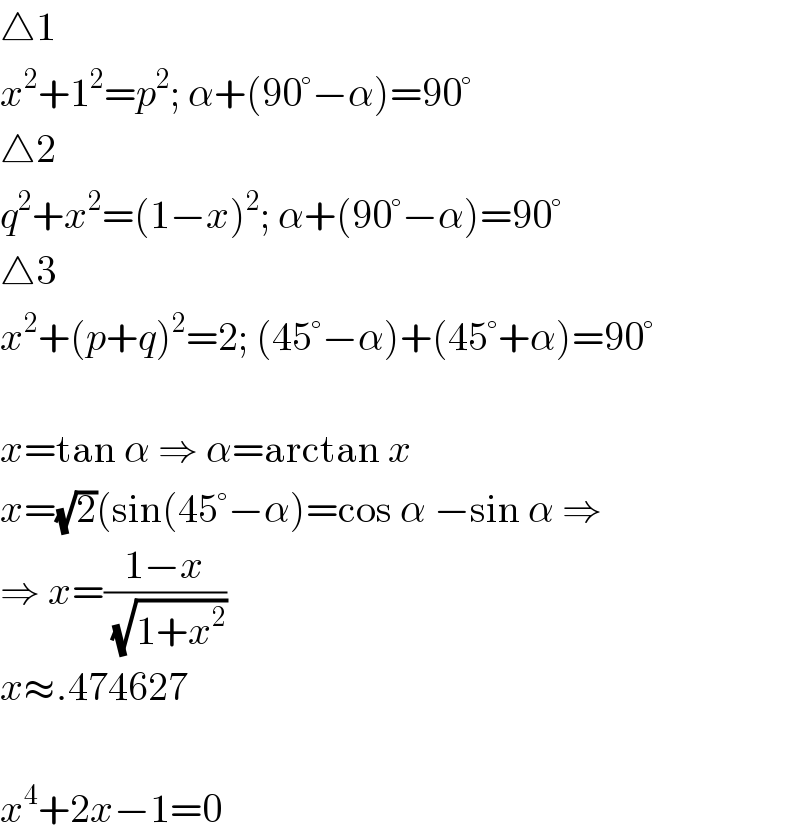
$$\bigtriangleup\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} ={p}^{\mathrm{2}} ;\:\alpha+\left(\mathrm{90}°−\alpha\right)=\mathrm{90}° \\ $$$$\bigtriangleup\mathrm{2} \\ $$$${q}^{\mathrm{2}} +{x}^{\mathrm{2}} =\left(\mathrm{1}−{x}\right)^{\mathrm{2}} ;\:\alpha+\left(\mathrm{90}°−\alpha\right)=\mathrm{90}° \\ $$$$\bigtriangleup\mathrm{3} \\ $$$${x}^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} =\mathrm{2};\:\left(\mathrm{45}°−\alpha\right)+\left(\mathrm{45}°+\alpha\right)=\mathrm{90}° \\ $$$$ \\ $$$${x}=\mathrm{tan}\:\alpha\:\Rightarrow\:\alpha=\mathrm{arctan}\:{x} \\ $$$${x}=\sqrt{\mathrm{2}}\left(\mathrm{sin}\left(\mathrm{45}°−\alpha\right)=\mathrm{cos}\:\alpha\:−\mathrm{sin}\:\alpha\:\Rightarrow\right. \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${x}\approx.\mathrm{474627} \\ $$$$ \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$
Commented by ajfour last updated on 06/Jul/18
$${Thank}\:{you}\:{Sir},\:{right}\:{answer}. \\ $$
Commented by MJS last updated on 06/Jul/18
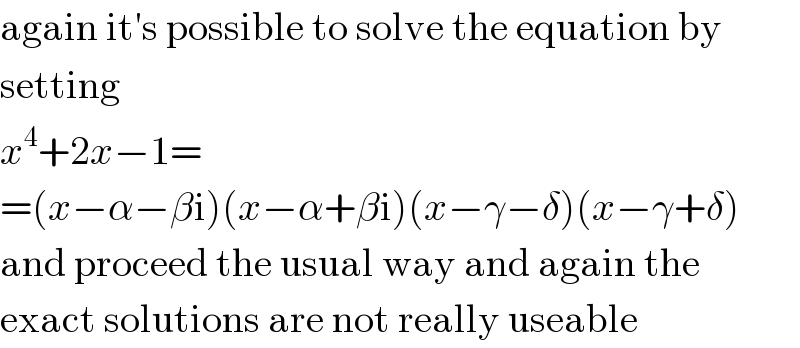
$$\mathrm{again}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{by} \\ $$$$\mathrm{setting} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}−\mathrm{1}= \\ $$$$=\left({x}−\alpha−\beta\mathrm{i}\right)\left({x}−\alpha+\beta\mathrm{i}\right)\left({x}−\gamma−\delta\right)\left({x}−\gamma+\delta\right) \\ $$$$\mathrm{and}\:\mathrm{proceed}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{way}\:\mathrm{and}\:\mathrm{again}\:\mathrm{the} \\ $$$$\mathrm{exact}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{not}\:\mathrm{really}\:\mathrm{useable} \\ $$
Answered by MrW3 last updated on 06/Jul/18
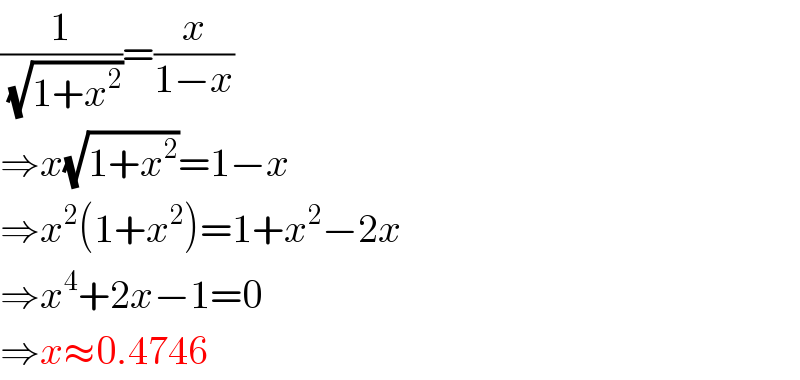
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\frac{{x}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }=\mathrm{1}−{x} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)=\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}\approx\mathrm{0}.\mathrm{4746} \\ $$
