Question Number 39379 by rahul 19 last updated on 05/Jul/18

Commented by MJS last updated on 06/Jul/18
![(1) ∣∣x∣−∣y∣∣=1 (2) 2a∣x∣∣y∣+1=2∣x∣+a∣y∣ (1) { ((y_1 =−∣x∣−1; range(y_1 )=]−∞; −1])),((y_2 =∣x∣+1; range(y_2 )=[1; +∞[)),((∣x∣≥1 { ((y_3 =−∣x∣+1; range(y_3 )=]−∞; 0])),((y_4 =∣x∣−1; range(y_4 )=[0; +∞[)) :})) :} (2) 2a∣x∣∣y∣−a∣y∣=2∣x∣−1 a∣y∣(2∣x∣−1)=2∣x∣−1 ∣y∣=(1/a) ⇒ { ((y_5 =−(1/a))),((y_6 =(1/a))) :} because range of y_1 and y_2 excludes ]−1; 1[ and they reach −1 and 1 respectively only once ⇒ ∣(1/a)∣>1 ⇒ ∣a∣<1](https://www.tinkutara.com/question/Q39493.png)
$$\left(\mathrm{1}\right)\:\:\:\:\:\mid\mid{x}\mid−\mid{y}\mid\mid=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\mathrm{2}{a}\mid{x}\mid\mid{y}\mid+\mathrm{1}=\mathrm{2}\mid{x}\mid+{a}\mid{y}\mid \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\begin{cases}{\left.{y}_{\mathrm{1}} \left.=−\mid{x}\mid−\mathrm{1};\:\mathrm{range}\left({y}_{\mathrm{1}} \right)=\right]−\infty;\:−\mathrm{1}\right]}\\{{y}_{\mathrm{2}} =\mid{x}\mid+\mathrm{1};\:\mathrm{range}\left({y}_{\mathrm{2}} \right)=\left[\mathrm{1};\:+\infty\left[\right.\right.}\\{\mid{x}\mid\geqslant\mathrm{1}\:\begin{cases}{\left.{y}_{\mathrm{3}} \left.=−\mid{x}\mid+\mathrm{1};\:\mathrm{range}\left({y}_{\mathrm{3}} \right)=\right]−\infty;\:\mathrm{0}\right]}\\{{y}_{\mathrm{4}} =\mid{x}\mid−\mathrm{1};\:\mathrm{range}\left({y}_{\mathrm{4}} \right)=\left[\mathrm{0};\:+\infty\left[\right.\right.}\end{cases}}\end{cases} \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\mathrm{2}{a}\mid{x}\mid\mid{y}\mid−{a}\mid{y}\mid=\mathrm{2}\mid{x}\mid−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{a}\mid{y}\mid\left(\mathrm{2}\mid{x}\mid−\mathrm{1}\right)=\mathrm{2}\mid{x}\mid−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mid{y}\mid=\frac{\mathrm{1}}{{a}}\:\Rightarrow\:\begin{cases}{{y}_{\mathrm{5}} =−\frac{\mathrm{1}}{{a}}}\\{{y}_{\mathrm{6}} =\frac{\mathrm{1}}{{a}}}\end{cases} \\ $$$$\left.\mathrm{because}\:\mathrm{range}\:\mathrm{of}\:{y}_{\mathrm{1}} \:\mathrm{and}\:{y}_{\mathrm{2}} \:\mathrm{excludes}\:\right]−\mathrm{1};\:\mathrm{1}\left[\right. \\ $$$$\mathrm{and}\:\mathrm{they}\:\mathrm{reach}\:−\mathrm{1}\:\mathrm{and}\:\mathrm{1}\:\mathrm{respectively}\:\mathrm{only} \\ $$$$\mathrm{once}\:\Rightarrow\:\mid\frac{\mathrm{1}}{{a}}\mid>\mathrm{1}\:\Rightarrow\:\mid{a}\mid<\mathrm{1} \\ $$
Commented by MJS last updated on 06/Jul/18
![a is not a number but its range is ]−1; 1[, so −3<3a<3 we can′t give a single value](https://www.tinkutara.com/question/Q39499.png)
$$\left.{a}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{number}\:\mathrm{but}\:\mathrm{its}\:\mathrm{range}\:\mathrm{is}\:\right]−\mathrm{1};\:\mathrm{1}\left[,\:\mathrm{so}\right. \\ $$$$−\mathrm{3}<\mathrm{3}{a}<\mathrm{3}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{give}\:\mathrm{a}\:\mathrm{single}\:\mathrm{value} \\ $$
Commented by rahul 19 last updated on 06/Jul/18
What's the value of 3a ?
Commented by rahul 19 last updated on 06/Jul/18
Ans. given is 2!
Commented by MJS last updated on 06/Jul/18

$$\mathrm{draw}\:\mathrm{these}\:\mathrm{functions},\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{given}\:\mathrm{answer} \\ $$$$\mathrm{is}\:\mathrm{wrong}.\:\mathrm{or}\:\mathrm{else}\:\mathrm{we}\:\mathrm{must}\:\mathrm{limit}\:\mathrm{the}\:\mathrm{allowed} \\ $$$$\mathrm{range}\:\mathrm{of}\:{a}\:\left(\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{such}\:\mathrm{limit}\:\mathrm{given}\right) \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Ok sir !
thanks ! ��
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18
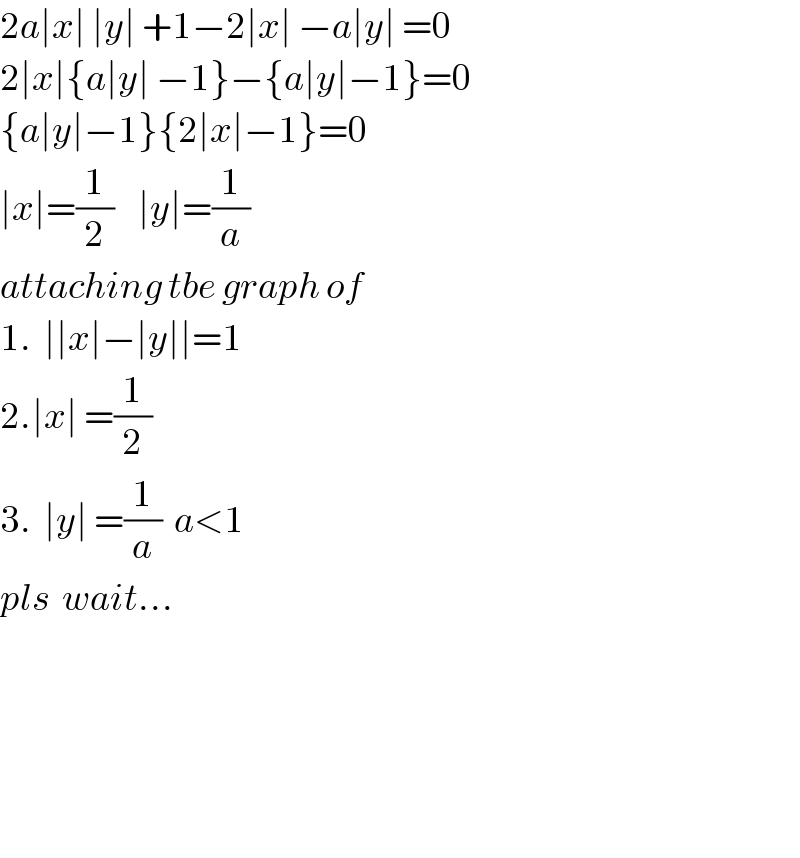
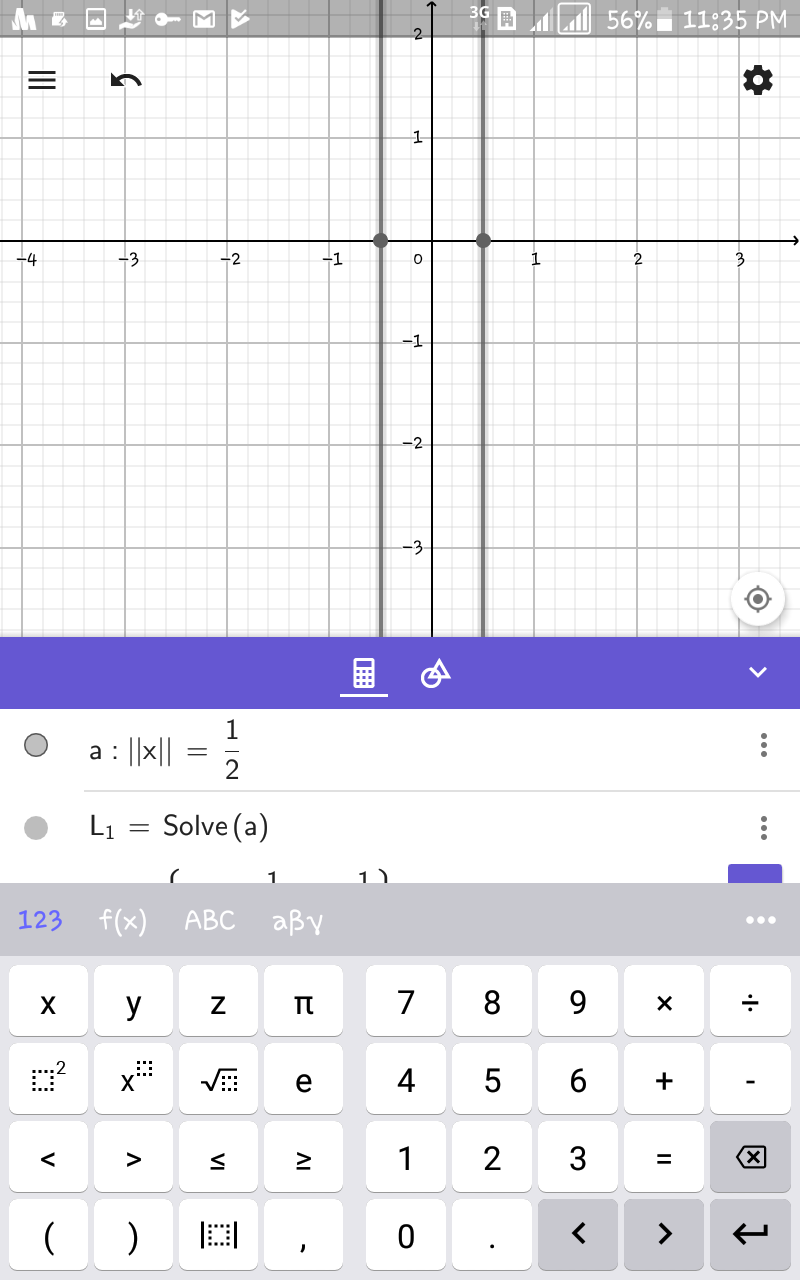
$$\mathrm{2}{a}\mid{x}\mid\:\mid{y}\mid\:+\mathrm{1}−\mathrm{2}\mid{x}\mid\:−{a}\mid{y}\mid\:=\mathrm{0} \\ $$$$\mathrm{2}\mid{x}\mid\left\{{a}\mid{y}\mid\:−\mathrm{1}\right\}−\left\{{a}\mid{y}\mid−\mathrm{1}\right\}=\mathrm{0} \\ $$$$\left\{{a}\mid{y}\mid−\mathrm{1}\right\}\left\{\mathrm{2}\mid{x}\mid−\mathrm{1}\right\}=\mathrm{0} \\ $$$$\mid{x}\mid=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\mid{y}\mid=\frac{\mathrm{1}}{{a}} \\ $$$${attaching}\:{tbe}\:{graph}\:{of} \\ $$$$\mathrm{1}.\:\:\mid\mid{x}\mid−\mid{y}\mid\mid=\mathrm{1} \\ $$$$\mathrm{2}.\mid{x}\mid\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}.\:\:\mid{y}\mid\:=\frac{\mathrm{1}}{{a}}\:\:{a}<\mathrm{1} \\ $$$${pls}\:\:{wait}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18