Question-39436

Question Number 39436 by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

Commented by ajfour last updated on 06/Jul/18

3φ = 90° ⇒ φ=30° Rsin 30° = asin θ ⇒ sin θ = (R/(2a)) ⇒ cos θ = ((√(4a^2 −R^2 ))/(2a)) bsin (180°−2φ−θ)=(R/2) ⇒ bsin (60°+θ)=(R/2) b = (R/(2[((√3)/2)cos θ+((sin θ)/2)])) =(R/( (√3)(((√(4a^2 −R^2 ))/(2a)))+(R/(2a)))) ⇒ b = ((2aR)/(R+(√(12a^2 −3R^2 )))) .

$$\mathrm{3}\phi\:=\:\mathrm{90}°\:\:\:\Rightarrow\:\:\phi=\mathrm{30}° \\ $$$${R}\mathrm{sin}\:\mathrm{30}°\:=\:{a}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\theta\:=\:\frac{{R}}{\mathrm{2}{a}}\:\:\Rightarrow\:\mathrm{cos}\:\theta\:=\:\frac{\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }}{\mathrm{2}{a}} \\ $$$${b}\mathrm{sin}\:\left(\mathrm{180}°−\mathrm{2}\phi−\theta\right)=\frac{{R}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{b}\mathrm{sin}\:\left(\mathrm{60}°+\theta\right)=\frac{{R}}{\mathrm{2}} \\ $$$$\:\:\:\boldsymbol{{b}}\:=\:\frac{\boldsymbol{{R}}}{\mathrm{2}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right]} \\ $$$$\:\:\:\:\:\:=\frac{{R}}{\:\sqrt{\mathrm{3}}\left(\frac{\sqrt{\mathrm{4}{a}^{\mathrm{2}} −{R}^{\mathrm{2}} }}{\mathrm{2}{a}}\right)+\frac{{R}}{\mathrm{2}{a}}} \\ $$$$\Rightarrow\:\:{b}\:=\:\frac{\mathrm{2}{aR}}{{R}+\sqrt{\mathrm{12}{a}^{\mathrm{2}} −\mathrm{3}{R}^{\mathrm{2}} }}\:. \\ $$

Answered by MJS last updated on 06/Jul/18

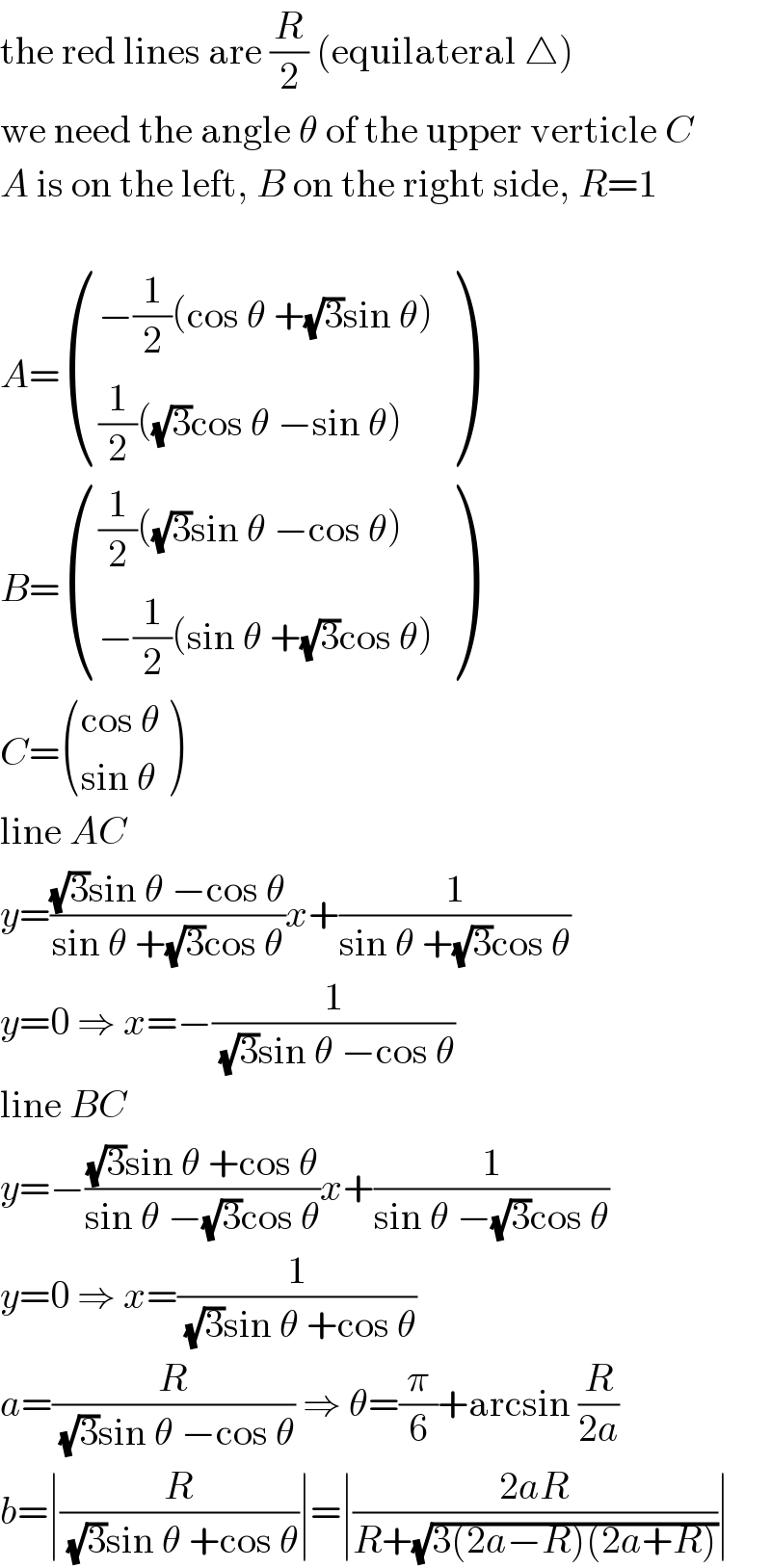
the red lines are (R/2) (equilateral △) we need the angle θ of the upper verticle C A is on the left, B on the right side, R=1 A= (((−(1/2)(cos θ +(√3)sin θ))),(((1/2)((√3)cos θ −sin θ))) ) B= ((((1/2)((√3)sin θ −cos θ))),((−(1/2)(sin θ +(√3)cos θ))) ) C= (((cos θ)),((sin θ)) ) line AC y=(((√3)sin θ −cos θ)/(sin θ +(√3)cos θ))x+(1/(sin θ +(√3)cos θ)) y=0 ⇒ x=−(1/( (√3)sin θ −cos θ)) line BC y=−(((√3)sin θ +cos θ)/(sin θ −(√3)cos θ))x+(1/(sin θ −(√3)cos θ)) y=0 ⇒ x=(1/( (√3)sin θ +cos θ)) a=(R/( (√3)sin θ −cos θ)) ⇒ θ=(π/6)+arcsin (R/(2a)) b=∣(R/( (√3)sin θ +cos θ))∣=∣((2aR)/(R+(√(3(2a−R)(2a+R)))))∣

$$\mathrm{the}\:\mathrm{red}\:\mathrm{lines}\:\mathrm{are}\:\frac{{R}}{\mathrm{2}}\:\left(\mathrm{equilateral}\:\bigtriangleup\right) \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{angle}\:\theta\:\mathrm{of}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{verticle}\:{C} \\ $$$${A}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left},\:{B}\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{side},\:{R}=\mathrm{1} \\ $$$$ \\ $$$${A}=\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\right)}\\{\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\:−\mathrm{sin}\:\theta\right)}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta\right)}\\{−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta\right)}\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{\mathrm{cos}\:\theta}\\{\mathrm{sin}\:\theta}\end{pmatrix} \\ $$$$\mathrm{line}\:{AC} \\ $$$${y}=\frac{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta}{x}+\frac{\mathrm{1}}{\mathrm{sin}\:\theta\:+\sqrt{\mathrm{3}}\mathrm{cos}\:\theta} \\ $$$${y}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta} \\ $$$$\mathrm{line}\:{BC} \\ $$$${y}=−\frac{\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta\:−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta}{x}+\frac{\mathrm{1}}{\mathrm{sin}\:\theta\:−\sqrt{\mathrm{3}}\mathrm{cos}\:\theta} \\ $$$${y}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta} \\ $$$${a}=\frac{{R}}{\:\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta}\:\Rightarrow\:\theta=\frac{\pi}{\mathrm{6}}+\mathrm{arcsin}\:\frac{{R}}{\mathrm{2}{a}} \\ $$$${b}=\mid\frac{{R}}{\:\sqrt{\mathrm{3}}\mathrm{sin}\:\theta\:+\mathrm{cos}\:\theta}\mid=\mid\frac{\mathrm{2}{aR}}{{R}+\sqrt{\mathrm{3}\left(\mathrm{2}{a}−{R}\right)\left(\mathrm{2}{a}+{R}\right)}}\mid \\ $$

Commented by ajfour last updated on 06/Jul/18

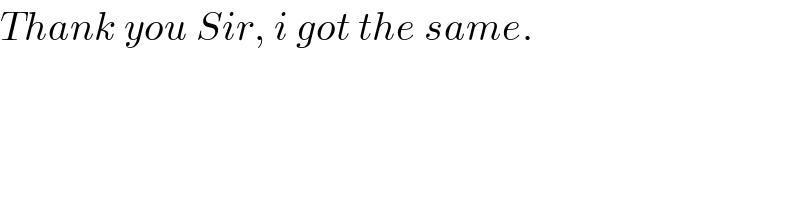
$${Thank}\:{you}\:{Sir},\:{i}\:{got}\:{the}\:{same}. \\ $$

Commented by MJS last updated on 06/Jul/18

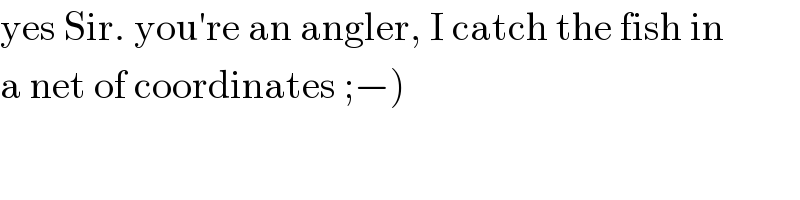
yes Sir. you′re an angler, I catch the fish in a net of coordinates ;−)

$$\mathrm{yes}\:\mathrm{Sir}.\:\mathrm{you}'\mathrm{re}\:\mathrm{an}\:\mathrm{angler},\:\mathrm{I}\:\mathrm{catch}\:\mathrm{the}\:\mathrm{fish}\:\mathrm{in} \\ $$$$\left.\mathrm{a}\:\mathrm{net}\:\mathrm{of}\:\mathrm{coordinates}\:;−\right) \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jul/18

Good anology! Really coordinate system is a net and an angler doesn′t use net for fishing!

$$\mathcal{G}{ood}\:{anology}!\:\mathrm{Really}\:\mathrm{coordinate}\:\mathrm{system} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{net}\:\mathrm{and}\:\mathrm{an}\:\mathrm{angler}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{use}\:\mathrm{net} \\ $$$$\mathrm{for}\:\mathrm{fishing}! \\ $$

Commented by behi83417@gmail.com last updated on 06/Jul/18

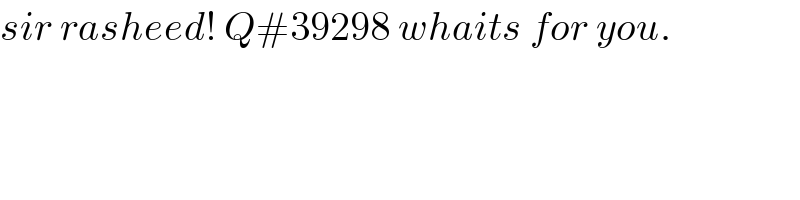
$${sir}\:{rasheed}!\:{Q}#\mathrm{39298}\:{whaits}\:{for}\:{you}. \\ $$

Commented by Rasheed.Sindhi last updated on 07/Jul/18

$$\mathrm{Too}\:\mathrm{hard}\:\mathrm{for}\:\mathrm{me}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply