Question Number 39469 by Raj Singh last updated on 06/Jul/18
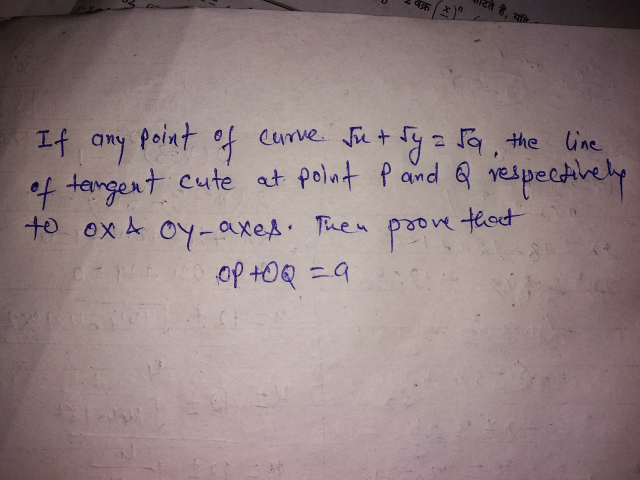
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jul/18
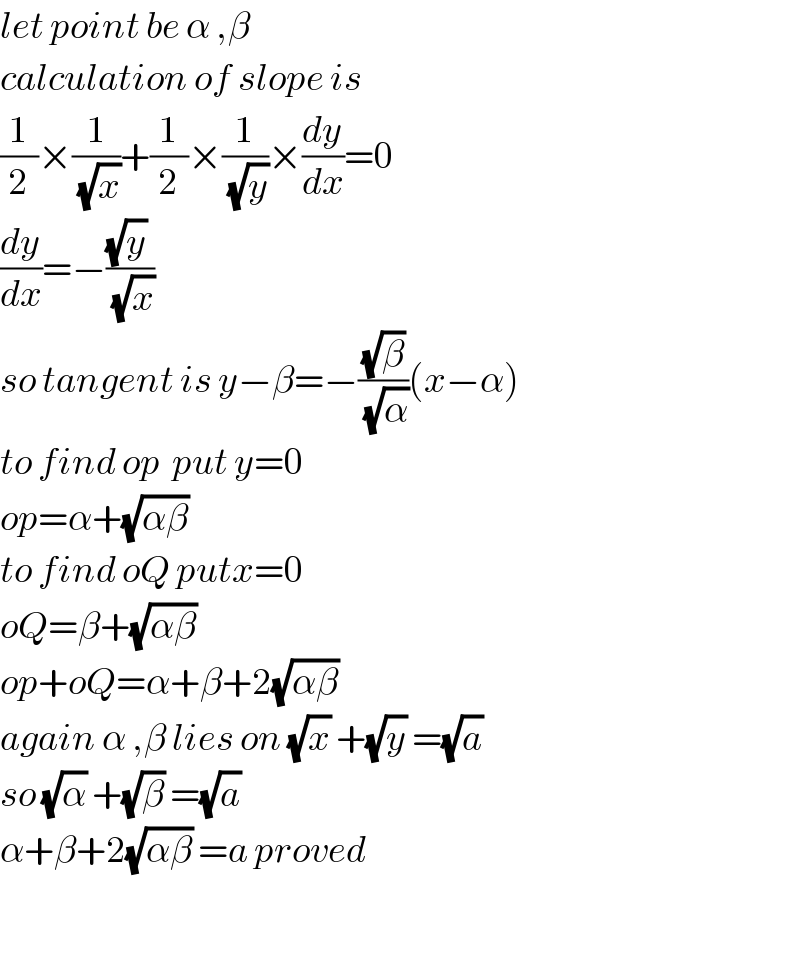
$${let}\:{point}\:{be}\:\alpha\:,\beta \\ $$$${calculation}\:{of}\:{slope}\:{is}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{{x}}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{{y}}}×\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\sqrt{{y}}\:}{\:\sqrt{{x}}} \\ $$$${so}\:{tangent}\:{is}\:{y}−\beta=−\frac{\sqrt{\beta}}{\:\sqrt{\alpha}}\left({x}−\alpha\right) \\ $$$${to}\:{find}\:{op}\:\:{put}\:{y}=\mathrm{0} \\ $$$${op}=\alpha+\sqrt{\alpha\beta}\: \\ $$$${to}\:{find}\:{oQ}\:{putx}=\mathrm{0} \\ $$$${oQ}=\beta+\sqrt{\alpha\beta} \\ $$$${op}+{oQ}=\alpha+\beta+\mathrm{2}\sqrt{\alpha\beta}\: \\ $$$${again}\:\alpha\:,\beta\:{lies}\:{on}\:\sqrt{{x}}\:+\sqrt{{y}}\:=\sqrt{{a}} \\ $$$${so}\:\sqrt{\alpha}\:+\sqrt{\beta}\:=\sqrt{{a}} \\ $$$$\alpha+\beta+\mathrm{2}\sqrt{\alpha\beta}\:={a}\:{proved} \\ $$$$ \\ $$
