Question Number 39475 by Raj Singh last updated on 06/Jul/18
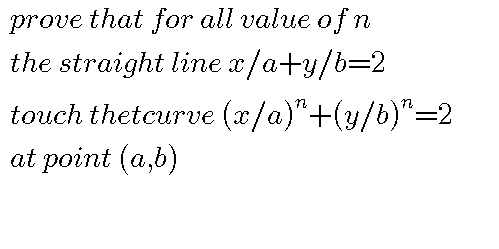
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jul/18

$$\:{calculatiin}\:{of}\:{slope}\:{at}\:\left({a},{b}\right)\:{w}.{r}.{t}\:\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{2}\:{is} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\frac{{dy}}{{dx}}}{{b}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{b}}{{a}} \\ $$$${calculation}\:{of}\:{slope}\:{w}.{r}.{t}\:\frac{{x}^{{n}} }{{a}^{{n}} }+\frac{{y}^{{n}} }{{b}^{{n}} }=\mathrm{2} \\ $$$$\frac{{nx}^{{n}−\mathrm{1}} }{{a}^{{n}} }+\frac{{ny}^{{n}−\mathrm{1}} \frac{{dy}}{{dx}}}{{b}^{{n}} }=\mathrm{0} \\ $$$${so}\:\left(\frac{{dy}}{{dx}\:}\right)_{\left({a},{b}\right)} \\ $$$$\frac{{na}^{{n}−\mathrm{1}} }{{a}^{{n}} }+\frac{{nb}^{{n}−\mathrm{1}} }{{b}^{{n}} }×\left(\frac{{dy}}{{dx}}\right)_{\left({a},{b}\right)} \:=\mathrm{0} \\ $$$$\left(\frac{{dy}}{{dx}}\right)_{\left({a},{b}\right)} ×\frac{{nb}^{{n}−\mathrm{1}} }{{b}^{{n}} }\:=−\frac{{na}^{{n}−\mathrm{1}} }{{a}^{{n}} } \\ $$$$\left(\frac{{dy}}{{dx}}\right)_{\left({a},{b}\right)} \:=−\frac{{b}}{{a}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{this}}\:\boldsymbol{{two}}\:\boldsymbol{{curve}}\:\boldsymbol{{has}}\:\boldsymbol{{a}}\:\boldsymbol{{common}}\:\boldsymbol{{tangent}} \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{point}}\:\left(\boldsymbol{{a}},\boldsymbol{{b}}\right)\:\:\:\boldsymbol{{that}}\:\boldsymbol{{means}}\:\boldsymbol{{they}}\:\boldsymbol{{touch}} \\ $$$$\boldsymbol{{each}}\:\boldsymbol{{other}}\:\boldsymbol{{at}}\:\left(\boldsymbol{{a}},\boldsymbol{{b}}\right) \\ $$$$ \\ $$
