Menu Close

Question-39559

Tinku Tara 0 Comments
Pin




Question Number 39559 by ajfour last updated on 07/Jul/18
Commented by ajfour last updated on 07/Jul/18
Find 𝛂 and radius r in terms of a.
$${Find}\:\boldsymbol{\alpha}\:{and}\:{radius}\:\boldsymbol{{r}}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}. \\ $$
Answered by MrW3 last updated on 08/Jul/18
2R×cos α=1+a ...(i) (R/(cos α))−1=(R+R tan α) sin α ...(ii) ⇒R=((1+a)/(2 cos α)) ((1+a)/(2 cos^2 α))−1=((1+a)/(2 cos α))(1+((sin α)/(cos α))) sin α ((1+a−2 cos^2 α)/(2 cos^2 α))=(((1+a)(cos α+sin α)sin α)/(2 cos^2 α)) 1+a−2 cos^2 α=(1+a)(sin α cos α+sin^2 α) 2[a−(2 cos^2 α−1)]=(1+a)(2sin α cos α−(1−2sin^2 α)+1) 2(a−cos 2α)=(1+a)(sin 2α−cos 2α+1) 2a−2 cos 2α=(1+a) sin 2α−(1+a) cos 2α+(1+a) (a+1) sin 2α−(a−1) cos 2α=a−1 ((a+1)/( (√((a+1)^2 +(a−1)^2 )))) sin 2α−((a−1)/( (√((a+1)^2 +(a−1)^2 )))) cos 2α=((a−1)/( (√((a+1)^2 +(a−1)^2 )))) ((a+1)/( (√(2(a^2 +1))))) sin 2α−((a−1)/( (√(2(a^2 +1))))) cos 2α=((a−1)/( (√(2(a^2 +1))))) cos θ sin 2α−sin θ cos 2α=sin θ sin (2α−θ)=sin θ ⇒2α−θ=θ ⇒α=θ=tan^(−1) ((a−1)/(a+1)) ⇒cos α=cos θ=((a+1)/( (√(2(a^2 +1))))) ⇒R=((1+a)/(2 cos α))=((1+a)/(2×((a+1)/( (√(2(a^2 +1)))))))=(√((a^2 +1)/2))
$$\mathrm{2}{R}×\mathrm{cos}\:\alpha=\mathrm{1}+{a}\:\:\:…\left({i}\right) \\ $$$$\frac{{R}}{\mathrm{cos}\:\alpha}−\mathrm{1}=\left({R}+{R}\:\mathrm{tan}\:\alpha\right)\:\mathrm{sin}\:\alpha\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}+{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha} \\ $$$$\frac{\mathrm{1}+{a}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha}−\mathrm{1}=\frac{\mathrm{1}+{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha}\left(\mathrm{1}+\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}\right)\:\mathrm{sin}\:\alpha \\ $$$$\frac{\mathrm{1}+{a}−\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha}=\frac{\left(\mathrm{1}+{a}\right)\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)\mathrm{sin}\:\alpha}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha} \\ $$$$\mathrm{1}+{a}−\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha=\left(\mathrm{1}+{a}\right)\left(\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha+\mathrm{sin}^{\mathrm{2}} \:\alpha\right) \\ $$$$\mathrm{2}\left[{a}−\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\right]=\left(\mathrm{1}+{a}\right)\left(\mathrm{2sin}\:\alpha\:\mathrm{cos}\:\alpha−\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\alpha\right)+\mathrm{1}\right) \\ $$$$\mathrm{2}\left({a}−\mathrm{cos}\:\mathrm{2}\alpha\right)=\left(\mathrm{1}+{a}\right)\left(\mathrm{sin}\:\mathrm{2}\alpha−\mathrm{cos}\:\mathrm{2}\alpha+\mathrm{1}\right) \\ $$$$\mathrm{2}{a}−\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\alpha=\left(\mathrm{1}+{a}\right)\:\mathrm{sin}\:\mathrm{2}\alpha−\left(\mathrm{1}+{a}\right)\:\mathrm{cos}\:\mathrm{2}\alpha+\left(\mathrm{1}+{a}\right) \\ $$$$\left({a}+\mathrm{1}\right)\:\mathrm{sin}\:\mathrm{2}\alpha−\left({a}−\mathrm{1}\right)\:\mathrm{cos}\:\mathrm{2}\alpha={a}−\mathrm{1} \\ $$$$\frac{{a}+\mathrm{1}}{\:\sqrt{\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\left({a}−\mathrm{1}\right)^{\mathrm{2}} }}\:\mathrm{sin}\:\mathrm{2}\alpha−\frac{{a}−\mathrm{1}}{\:\sqrt{\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\left({a}−\mathrm{1}\right)^{\mathrm{2}} }}\:\mathrm{cos}\:\mathrm{2}\alpha=\frac{{a}−\mathrm{1}}{\:\sqrt{\left({a}+\mathrm{1}\right)^{\mathrm{2}} +\left({a}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\frac{{a}+\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}\:\mathrm{sin}\:\mathrm{2}\alpha−\frac{{a}−\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}\:\mathrm{cos}\:\mathrm{2}\alpha=\frac{{a}−\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}} \\ $$$$\mathrm{cos}\:\theta\:\mathrm{sin}\:\mathrm{2}\alpha−\mathrm{sin}\:\theta\:\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{sin}\:\:\theta \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\alpha−\theta\right)=\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{2}\alpha−\theta=\theta \\ $$$$\Rightarrow\alpha=\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{a}−\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\mathrm{cos}\:\theta=\frac{{a}+\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}+{a}}{\mathrm{2}\:\mathrm{cos}\:\alpha}=\frac{\mathrm{1}+{a}}{\mathrm{2}×\frac{{a}+\mathrm{1}}{\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{1}\right)}}}=\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 08/Jul/18
Correct Sir, thanks; i thought you would make it shorter than my solution; its almost the same length.
$${Correct}\:{Sir},\:{thanks};\:{i}\:{thought} \\ $$$${you}\:{would}\:{make}\:{it}\:{shorter}\:{than} \\ $$$${my}\:{solution};\:{its}\:{almost}\:{the}\:{same} \\ $$$${length}. \\ $$
Answered by ajfour last updated on 08/Jul/18
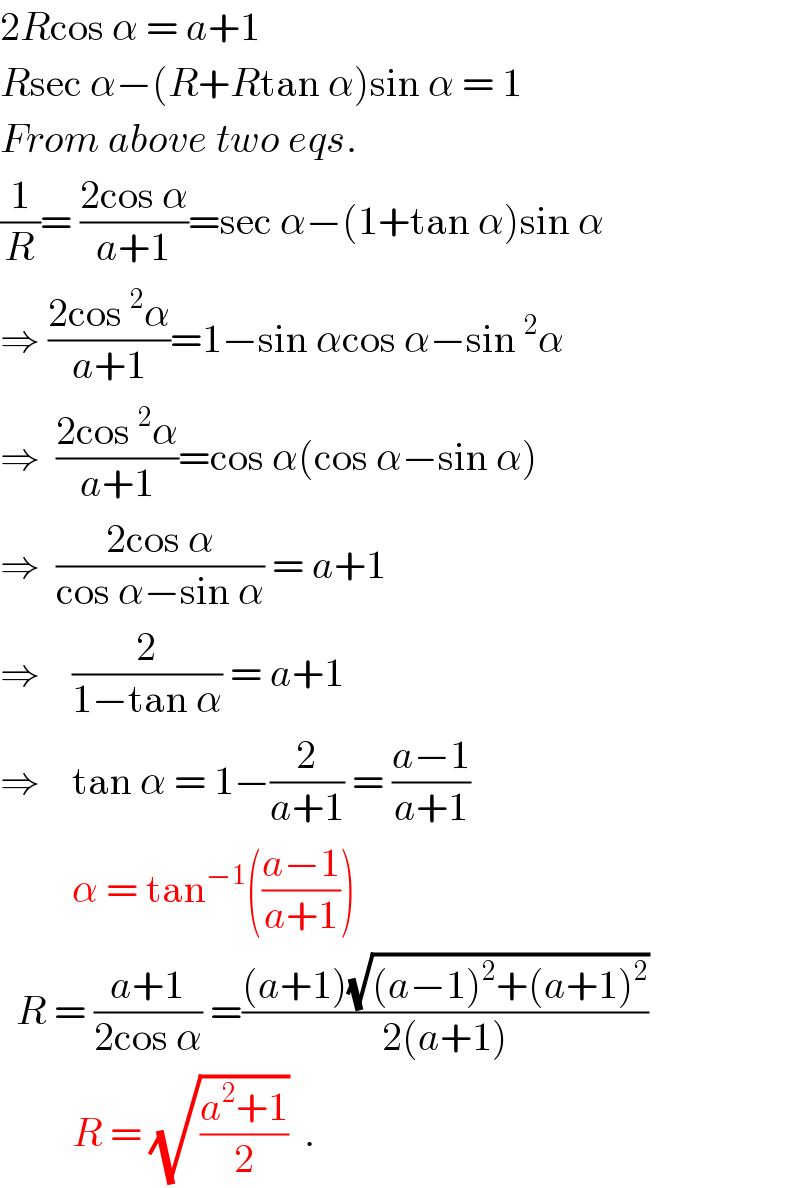
2Rcos α = a+1 Rsec α−(R+Rtan α)sin α = 1 From above two eqs. (1/R)= ((2cos α)/(a+1))=sec α−(1+tan α)sin α ⇒ ((2cos^2 α)/(a+1))=1−sin αcos α−sin^2 α ⇒ ((2cos^2 α)/(a+1))=cos α(cos α−sin α) ⇒ ((2cos α)/(cos α−sin α)) = a+1 ⇒ (2/(1−tan α)) = a+1 ⇒ tan α = 1−(2/(a+1)) = ((a−1)/(a+1)) α = tan^(−1) (((a−1)/(a+1))) R = ((a+1)/(2cos α)) =(((a+1)(√((a−1)^2 +(a+1)^2 )))/(2(a+1))) R = (√((a^2 +1)/2)) .
$$\mathrm{2}{R}\mathrm{cos}\:\alpha\:=\:{a}+\mathrm{1} \\ $$$${R}\mathrm{sec}\:\alpha−\left({R}+{R}\mathrm{tan}\:\alpha\right)\mathrm{sin}\:\alpha\:=\:\mathrm{1} \\ $$$${From}\:{above}\:{two}\:{eqs}. \\ $$$$\frac{\mathrm{1}}{{R}}=\:\frac{\mathrm{2cos}\:\alpha}{{a}+\mathrm{1}}=\mathrm{sec}\:\alpha−\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\:\frac{\mathrm{2cos}\:^{\mathrm{2}} \alpha}{{a}+\mathrm{1}}=\mathrm{1}−\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha−\mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\Rightarrow\:\:\frac{\mathrm{2cos}\:^{\mathrm{2}} \alpha}{{a}+\mathrm{1}}=\mathrm{cos}\:\alpha\left(\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{2cos}\:\alpha}{\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha}\:=\:{a}+\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−\mathrm{tan}\:\alpha}\:=\:{a}+\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\mathrm{tan}\:\alpha\:=\:\mathrm{1}−\frac{\mathrm{2}}{{a}+\mathrm{1}}\:=\:\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\right) \\ $$$$\:\:{R}\:=\:\frac{{a}+\mathrm{1}}{\mathrm{2cos}\:\alpha}\:=\frac{\left({a}+\mathrm{1}\right)\sqrt{\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\left({a}+\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}\left({a}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:{R}\:=\:\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}}\:\:. \\ $$
Commented by MrW3 last updated on 08/Jul/18
very nice sir!
$${very}\:{nice}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *