Question Number 39582 by Raj Singh last updated on 08/Jul/18
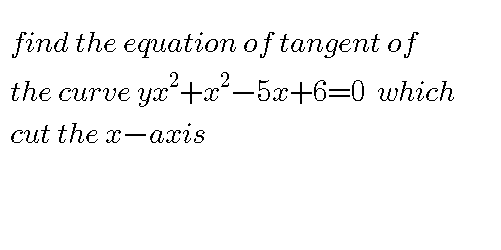
Answered by MrW3 last updated on 08/Jul/18
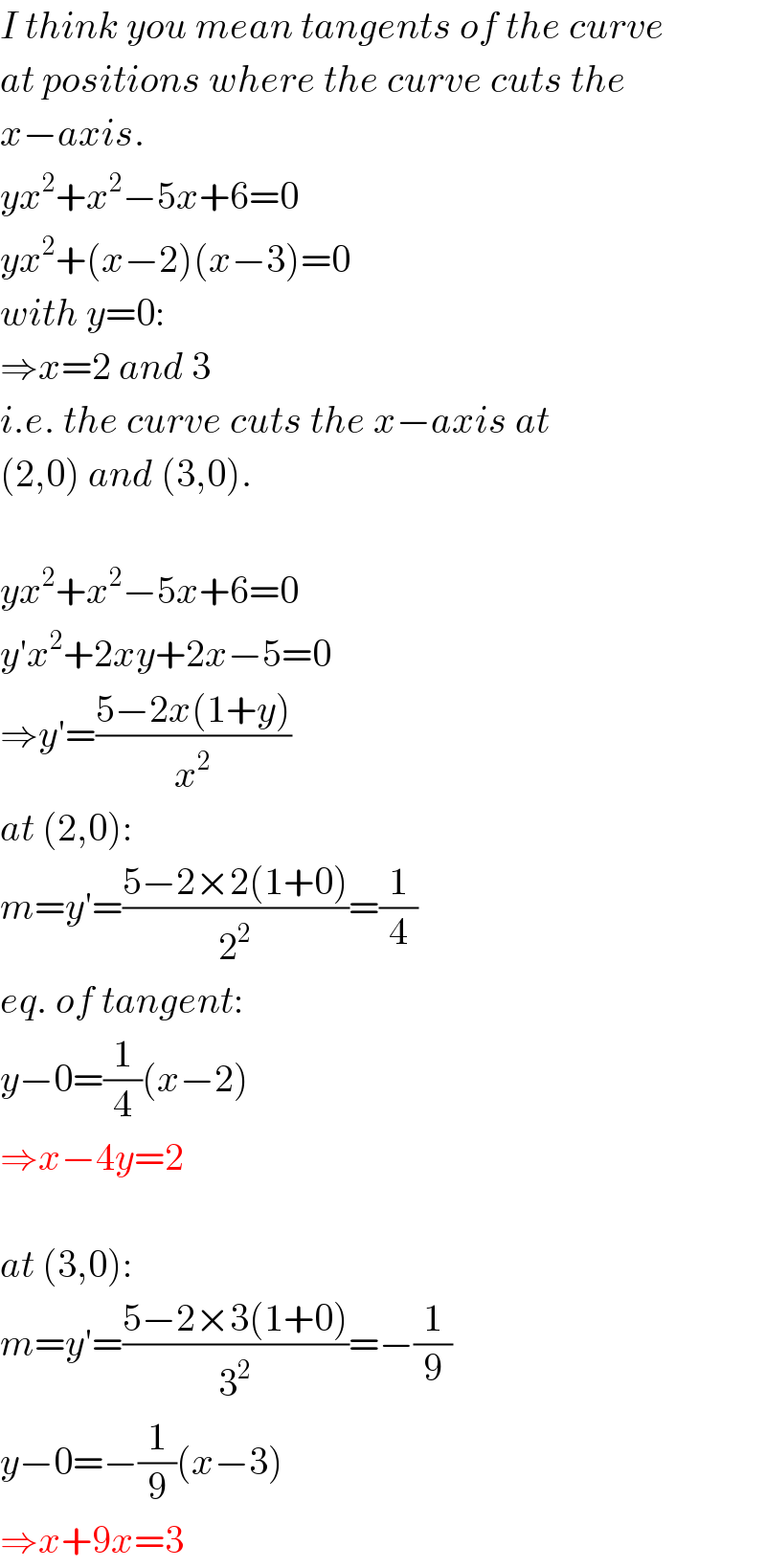
$${I}\:{think}\:{you}\:{mean}\:{tangents}\:{of}\:{the}\:{curve} \\ $$$${at}\:{positions}\:{where}\:{the}\:{curve}\:{cuts}\:{the} \\ $$$${x}−{axis}. \\ $$$${yx}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}=\mathrm{0} \\ $$$${yx}^{\mathrm{2}} +\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$${with}\:{y}=\mathrm{0}: \\ $$$$\Rightarrow{x}=\mathrm{2}\:{and}\:\mathrm{3} \\ $$$${i}.{e}.\:{the}\:{curve}\:{cuts}\:{the}\:{x}−{axis}\:{at} \\ $$$$\left(\mathrm{2},\mathrm{0}\right)\:{and}\:\left(\mathrm{3},\mathrm{0}\right). \\ $$$$ \\ $$$${yx}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}=\mathrm{0} \\ $$$${y}'{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{2}{x}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{y}'=\frac{\mathrm{5}−\mathrm{2}{x}\left(\mathrm{1}+{y}\right)}{{x}^{\mathrm{2}} } \\ $$$${at}\:\left(\mathrm{2},\mathrm{0}\right): \\ $$$${m}={y}'=\frac{\mathrm{5}−\mathrm{2}×\mathrm{2}\left(\mathrm{1}+\mathrm{0}\right)}{\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${eq}.\:{of}\:{tangent}: \\ $$$${y}−\mathrm{0}=\frac{\mathrm{1}}{\mathrm{4}}\left({x}−\mathrm{2}\right) \\ $$$$\Rightarrow{x}−\mathrm{4}{y}=\mathrm{2} \\ $$$$ \\ $$$${at}\:\left(\mathrm{3},\mathrm{0}\right): \\ $$$${m}={y}'=\frac{\mathrm{5}−\mathrm{2}×\mathrm{3}\left(\mathrm{1}+\mathrm{0}\right)}{\mathrm{3}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${y}−\mathrm{0}=−\frac{\mathrm{1}}{\mathrm{9}}\left({x}−\mathrm{3}\right) \\ $$$$\Rightarrow{x}+\mathrm{9}{x}=\mathrm{3} \\ $$
