Question Number 39612 by Tinkutara last updated on 08/Jul/18

Commented by MJS last updated on 08/Jul/18
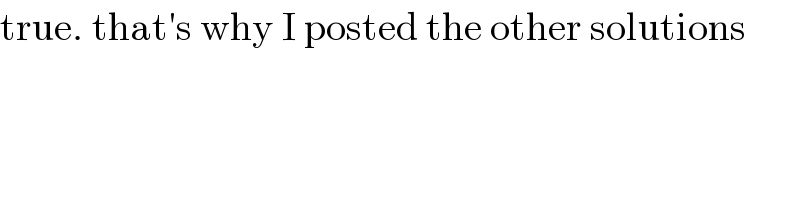
$$\mathrm{true}.\:\mathrm{that}'\mathrm{s}\:\mathrm{why}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{the}\:\mathrm{other}\:\mathrm{solutions} \\ $$
Commented by MJS last updated on 08/Jul/18
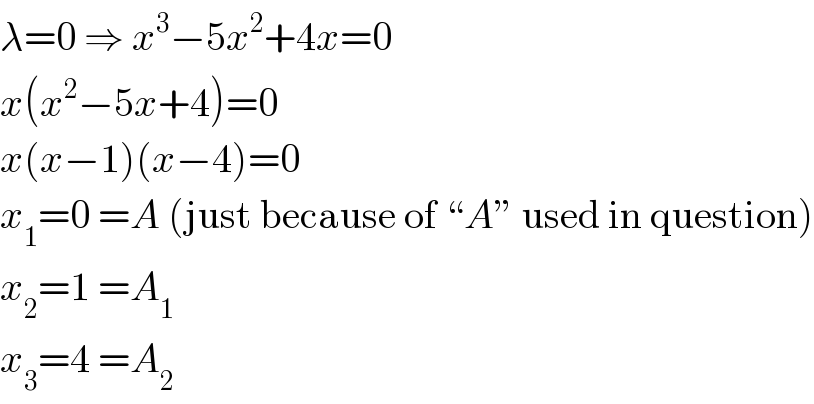
$$\lambda=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}=\mathrm{0} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}\:={A}\:\left(\mathrm{just}\:\mathrm{because}\:\mathrm{of}\:“{A}''\:\mathrm{used}\:\mathrm{in}\:\mathrm{question}\right) \\ $$$${x}_{\mathrm{2}} =\mathrm{1}\:={A}_{\mathrm{1}} \\ $$$${x}_{\mathrm{3}} =\mathrm{4}\:={A}_{\mathrm{2}} \\ $$
Commented by Tinkutara last updated on 08/Jul/18
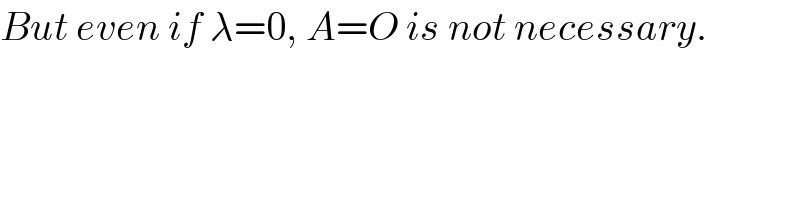
$${But}\:{even}\:{if}\:\lambda=\mathrm{0},\:{A}={O}\:{is}\:{not}\:{necessary}. \\ $$
Commented by Tinkutara last updated on 08/Jul/18
Thank you very much Sir! I got the answer. ��������
Answered by MJS last updated on 08/Jul/18
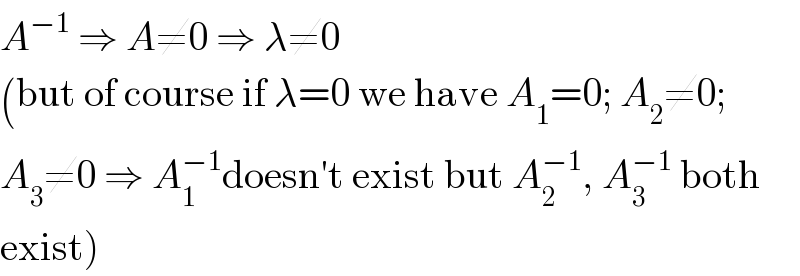
$${A}^{−\mathrm{1}} \:\Rightarrow\:{A}\neq\mathrm{0}\:\Rightarrow\:\lambda\neq\mathrm{0} \\ $$$$\left(\mathrm{but}\:\mathrm{of}\:\mathrm{course}\:\mathrm{if}\:\lambda=\mathrm{0}\:\mathrm{we}\:\mathrm{have}\:{A}_{\mathrm{1}} =\mathrm{0};\:{A}_{\mathrm{2}} \neq\mathrm{0};\right. \\ $$$${A}_{\mathrm{3}} \neq\mathrm{0}\:\Rightarrow\:{A}_{\mathrm{1}} ^{−\mathrm{1}} \mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\mathrm{but}\:{A}_{\mathrm{2}} ^{−\mathrm{1}} ,\:{A}_{\mathrm{3}} ^{−\mathrm{1}} \:\mathrm{both} \\ $$$$\left.\mathrm{exist}\right) \\ $$
Commented by Tinkutara last updated on 08/Jul/18
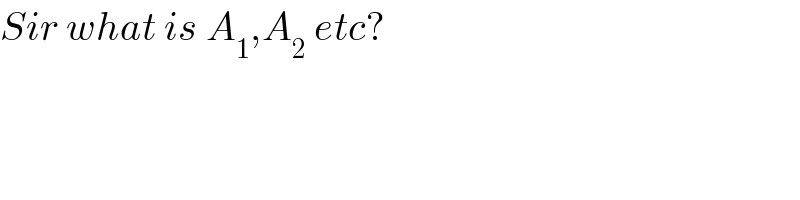
$${Sir}\:{what}\:{is}\:{A}_{\mathrm{1}} ,{A}_{\mathrm{2}} \:{etc}? \\ $$
