Question Number 39626 by ajfour last updated on 08/Jul/18
Commented by ajfour last updated on 09/Jul/18
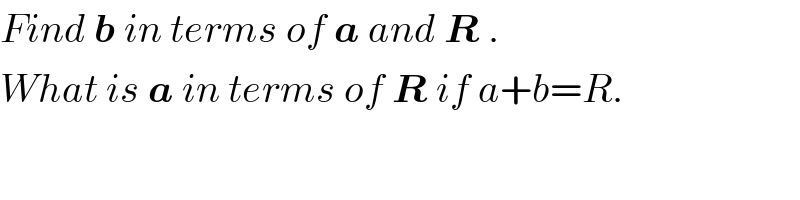
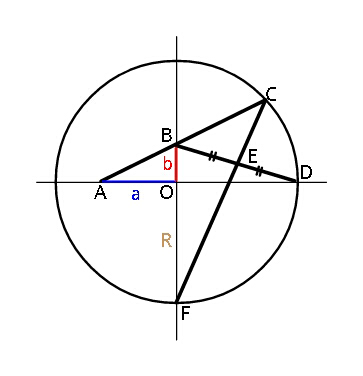
$${Find}\:\boldsymbol{{b}}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{R}}\:. \\ $$$${What}\:{is}\:\boldsymbol{{a}}\:{in}\:{terms}\:{of}\:\boldsymbol{{R}}\:{if}\:{a}+{b}={R}. \\ $$
Answered by ajfour last updated on 09/Jul/18
![eq. of ABC : −(x/a)+(y/b)=1 ⇒ y = b(1+(x/a)) eq. of circle: x^2 +y^2 =R^2 Let C≡(h,k) h^2 +b^2 (1+(h/a))^2 =R^2 ....(i) E((R/2), (b/2)) lies in line CEF eq. of CEF y=((((b/2)+R)/(R/2)))x−R C lies on both lines, hence b(1+(h/a))=((b/R)+2)h−R h((b/R)−(b/a)+2)=b+R h= ((b+R)/(((b/R)−(b/a)+2))) let (b/a)=z and (R/a)=p then h = ((a(z+p))/((z/p)−z+2)) = ((a(pz+p^2 ))/((1−p)z+2p)) substituting in (i) [((a(pz+p^2 ))/((1−p)z+2p))]^2 +b^2 [1+((pz+p^2 )/((1−p)z+2p))]^2 =R^2 [(((pz+p^2 ))/((1−p)z+2p))]^2 +z^2 [1+((pz+p^2 )/((1−p)z+2p))]^2 =p^2 solving above eq. we would get z = (b/a) in terms of p =(R/a) but if a+b=R then a+az = ap ⇒ z = p−1 ⇒ ((p^2 (2p−1)^2 )/([2p−(1−p)^2 ]^2 )) +(p−1)^2 [1+((p(2p−1))/(2p−(1−p)^2 ))]^2 =p^2 p^2 (2p−1)^2 +(p−1)^2 (p^2 +3p−1)^2 =p^2 (4p−1−p^2 )^2 p^3 (6p−p^2 −2)(2−p)=(p^3 +2p^2 −4p+1)^2 ⇒ p^6 −8p^5 +14p^4 −4p^3 =p^6 +4p^4 +16p^2 +1+4p^5 −16p^3 −8p−8p^4 +4p^2 +2p^3 ⇒ 12p^5 −18p^4 −10p^3 +20p^2 −8p+1=0 ⇒ p ≈ 1.49438 and (a/R)=(1/p) ⇒ a≈ 0.669R .](https://www.tinkutara.com/question/Q39646.png)
$${eq}.\:{of}\:{ABC}\::\:\:\:\:\:−\frac{{x}}{{a}}+\frac{{y}}{{b}}=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\:\:\:{y}\:=\:{b}\left(\mathrm{1}+\frac{{x}}{{a}}\right) \\ $$$${eq}.\:{of}\:{circle}:\:\:\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${Let}\:{C}\equiv\left({h},{k}\right) \\ $$$${h}^{\mathrm{2}} +{b}^{\mathrm{2}} \left(\mathrm{1}+\frac{{h}}{{a}}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:\:\:\:\:\:….\left({i}\right) \\ $$$${E}\left(\frac{{R}}{\mathrm{2}},\:\frac{{b}}{\mathrm{2}}\right)\:\:{lies}\:{in}\:{line}\:{CEF} \\ $$$${eq}.\:{of}\:{CEF}\: \\ $$$$\:\:\:\:\:\:\:{y}=\left(\frac{\frac{{b}}{\mathrm{2}}+{R}}{{R}/\mathrm{2}}\right){x}−{R} \\ $$$${C}\:{lies}\:{on}\:{both}\:{lines},\:{hence} \\ $$$${b}\left(\mathrm{1}+\frac{{h}}{{a}}\right)=\left(\frac{{b}}{{R}}+\mathrm{2}\right){h}−{R} \\ $$$${h}\left(\frac{{b}}{{R}}−\frac{{b}}{{a}}+\mathrm{2}\right)={b}+{R} \\ $$$${h}=\:\frac{{b}+{R}}{\left(\frac{{b}}{{R}}−\frac{{b}}{{a}}+\mathrm{2}\right)} \\ $$$${let}\:\frac{{b}}{{a}}={z}\:\:\:\:{and}\:\:\frac{{R}}{{a}}={p} \\ $$$${then}\:\:\:\boldsymbol{{h}}\:=\:\frac{\boldsymbol{{a}}\left(\boldsymbol{{z}}+\boldsymbol{{p}}\right)}{\frac{\boldsymbol{{z}}}{\boldsymbol{{p}}}−\boldsymbol{{z}}+\mathrm{2}}\:=\:\frac{\boldsymbol{{a}}\left(\boldsymbol{{pz}}+\boldsymbol{{p}}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\boldsymbol{{p}}\right)\boldsymbol{{z}}+\mathrm{2}\boldsymbol{{p}}} \\ $$$${substituting}\:{in}\:\left({i}\right) \\ $$$$\:\:\left[\frac{{a}\left({pz}+{p}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{p}\right){z}+\mathrm{2}{p}}\right]^{\mathrm{2}} +{b}^{\mathrm{2}} \left[\mathrm{1}+\frac{{pz}+{p}^{\mathrm{2}} }{\left(\mathrm{1}−{p}\right){z}+\mathrm{2}{p}}\right]^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\:\:\left[\frac{\left({pz}+{p}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{p}\right){z}+\mathrm{2}{p}}\right]^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} \left[\mathrm{1}+\frac{{pz}+{p}^{\mathrm{2}} }{\left(\mathrm{1}−{p}\right){z}+\mathrm{2}{p}}\right]^{\mathrm{2}} =\boldsymbol{{p}}^{\mathrm{2}} \\ $$$${solving}\:{above}\:{eq}.\:{we}\:{would}\:{get} \\ $$$$\:\:\:\:\:\:\boldsymbol{{z}}\:=\:\frac{\boldsymbol{{b}}}{\boldsymbol{{a}}}\:{in}\:{terms}\:{of}\:\boldsymbol{{p}}\:=\frac{\boldsymbol{{R}}}{\boldsymbol{{a}}} \\ $$$${but}\:{if}\:{a}+{b}={R}\:\:{then}\:\:{a}+{az}\:=\:{ap} \\ $$$$\Rightarrow\:\:\:\:\:{z}\:=\:{p}−\mathrm{1} \\ $$$$\Rightarrow\:\:\:\frac{{p}^{\mathrm{2}} \left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{2}} }{\left[\mathrm{2}{p}−\left(\mathrm{1}−{p}\right)^{\mathrm{2}} \right]^{\mathrm{2}} }\:+\left({p}−\mathrm{1}\right)^{\mathrm{2}} \:\left[\mathrm{1}+\frac{{p}\left(\mathrm{2}{p}−\mathrm{1}\right)}{\mathrm{2}{p}−\left(\mathrm{1}−{p}\right)^{\mathrm{2}} }\right]^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} \left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{2}} +\left({p}−\mathrm{1}\right)^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{3}{p}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={p}^{\mathrm{2}} \left(\mathrm{4}{p}−\mathrm{1}−{p}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{3}} \left(\mathrm{6}{p}−{p}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{2}−{p}\right)=\left({p}^{\mathrm{3}} +\mathrm{2}{p}^{\mathrm{2}} −\mathrm{4}{p}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{p}^{\mathrm{6}} −\mathrm{8}{p}^{\mathrm{5}} +\mathrm{14}{p}^{\mathrm{4}} −\mathrm{4}{p}^{\mathrm{3}} ={p}^{\mathrm{6}} +\mathrm{4}{p}^{\mathrm{4}} +\mathrm{16}{p}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:+\mathrm{1}+\mathrm{4}{p}^{\mathrm{5}} −\mathrm{16}{p}^{\mathrm{3}} −\mathrm{8}{p}−\mathrm{8}{p}^{\mathrm{4}} +\mathrm{4}{p}^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{12}{p}^{\mathrm{5}} −\mathrm{18}{p}^{\mathrm{4}} −\mathrm{10}{p}^{\mathrm{3}} +\mathrm{20}{p}^{\mathrm{2}} −\mathrm{8}{p}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\boldsymbol{{p}}\:\approx\:\mathrm{1}.\mathrm{49438} \\ $$$$\:\:\:\:{and}\:\:\:\frac{\boldsymbol{{a}}}{\boldsymbol{{R}}}=\frac{\mathrm{1}}{\boldsymbol{{p}}}\:\:\Rightarrow\:\:\boldsymbol{{a}}\approx\:\mathrm{0}.\mathrm{669}{R}\:. \\ $$
Commented by ajfour last updated on 09/Jul/18

$${MrW}\mathrm{3}\:{Sir},\:{please}\:{help}\:{check}\:{this} \\ $$$${solution}.. \\ $$
Commented by MrW3 last updated on 10/Jul/18
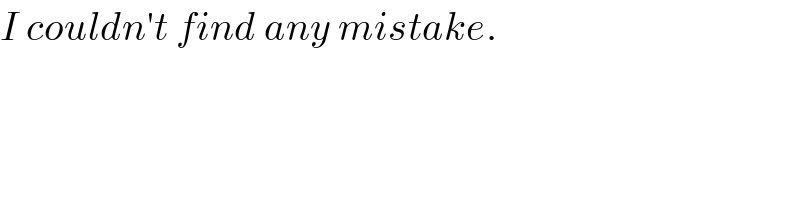
$${I}\:{couldn}'{t}\:{find}\:{any}\:{mistake}. \\ $$
Commented by ajfour last updated on 10/Jul/18
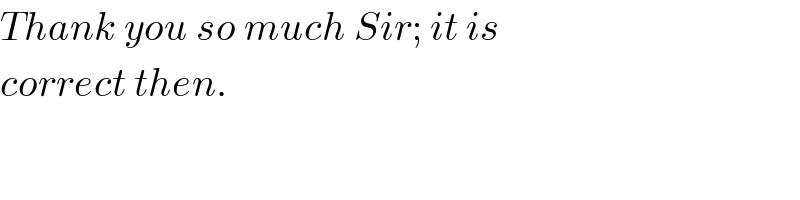
$${Thank}\:{you}\:{so}\:{much}\:{Sir};\:{it}\:{is} \\ $$$${correct}\:{then}. \\ $$
Answered by MJS last updated on 10/Jul/18
![R=1 A= (((−a)),(0) )B= ((0),(b) ) D= ((1),(0) ) E= (((1/2)),((b/2)) ) F= ((0),((−1)) ) line AB l_1 : y=(b/a)x+b line EF l_2 : y=(b+2)x−1 C=l_1 ∩l_2 = ((((a(b+1))/(a(b+2)−b))),((((a(b+2)+1)b)/(a(b+2)−b))) ) C on circle x^2 +y^2 −1=0 (I) ((a(b+1)(a(b^3 +3b^2 +b−3)+2b(b+2)))/((a(b+2)−b)^2 ))=0 [a=0 ∨ b=−1 not of further interest] [a(b+2)−b≠0 ⇒ a≠(b/(b+2)) ⇔ b≠((2a)/(1−a))] this can easily be solved for a a=((2b(b+2))/(3−b−3b^2 −b^3 )) ⇒ C= ((((2(b+2))/(b^2 +4b+5))),((((b+1)(b+3))/(b^2 +4b+5))) ) but for b it leads to b^3 +((3a+2)/a)b^2 +((a+4)/a)b−3=0 which can′t be generally solved with a+b=1 ⇒ b=1−a we get (I) ((a(a−2)(a^4 −6a^3 +8a^2 +6a−6))/((a^2 −4a+1)^2 ))=0 [a=0 ∨ a=2 not of further interest] [a^2 −4a+1≠0 ⇒ a≠2−(√3) ∧ a≠2+(√3)] a^4 −6a^3 +8a^2 +6a−6=0 again this can be exactly solved but with the usual difficulties, approximately we get a≈.669174 [a≈−.895728 not of further interest]](https://www.tinkutara.com/question/Q39723.png)
$${R}=\mathrm{1} \\ $$$${A}=\begin{pmatrix}{−{a}}\\{\mathrm{0}}\end{pmatrix}{B}=\begin{pmatrix}{\mathrm{0}}\\{{b}}\end{pmatrix}\:{D}=\begin{pmatrix}{\mathrm{1}}\\{\mathrm{0}}\end{pmatrix}\:{E}=\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}}\\{\frac{{b}}{\mathrm{2}}}\end{pmatrix}\:\:{F}=\begin{pmatrix}{\mathrm{0}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{line}\:{AB} \\ $$$${l}_{\mathrm{1}} :\:{y}=\frac{{b}}{{a}}{x}+{b} \\ $$$$\mathrm{line}\:{EF} \\ $$$${l}_{\mathrm{2}} :\:{y}=\left({b}+\mathrm{2}\right){x}−\mathrm{1} \\ $$$${C}={l}_{\mathrm{1}} \cap{l}_{\mathrm{2}} =\begin{pmatrix}{\frac{{a}\left({b}+\mathrm{1}\right)}{{a}\left({b}+\mathrm{2}\right)−{b}}}\\{\frac{\left({a}\left({b}+\mathrm{2}\right)+\mathrm{1}\right){b}}{{a}\left({b}+\mathrm{2}\right)−{b}}}\end{pmatrix} \\ $$$${C}\:\mathrm{on}\:\mathrm{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{I}\right)\:\:\frac{{a}\left({b}+\mathrm{1}\right)\left({a}\left({b}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{2}} +{b}−\mathrm{3}\right)+\mathrm{2}{b}\left({b}+\mathrm{2}\right)\right)}{\left({a}\left({b}+\mathrm{2}\right)−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{a}=\mathrm{0}\:\vee\:{b}=−\mathrm{1}\:\mathrm{not}\:\mathrm{of}\:\mathrm{further}\:\mathrm{interest}\right] \\ $$$$\:\:\:\:\:\left[{a}\left({b}+\mathrm{2}\right)−{b}\neq\mathrm{0}\:\Rightarrow\:{a}\neq\frac{{b}}{{b}+\mathrm{2}}\:\Leftrightarrow\:{b}\neq\frac{\mathrm{2}{a}}{\mathrm{1}−{a}}\right] \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:{a} \\ $$$${a}=\frac{\mathrm{2}{b}\left({b}+\mathrm{2}\right)}{\mathrm{3}−{b}−\mathrm{3}{b}^{\mathrm{2}} −{b}^{\mathrm{3}} }\:\Rightarrow\:{C}=\begin{pmatrix}{\frac{\mathrm{2}\left({b}+\mathrm{2}\right)}{{b}^{\mathrm{2}} +\mathrm{4}{b}+\mathrm{5}}}\\{\frac{\left({b}+\mathrm{1}\right)\left({b}+\mathrm{3}\right)}{{b}^{\mathrm{2}} +\mathrm{4}{b}+\mathrm{5}}}\end{pmatrix} \\ $$$$\mathrm{but}\:\mathrm{for}\:{b}\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to} \\ $$$${b}^{\mathrm{3}} +\frac{\mathrm{3}{a}+\mathrm{2}}{{a}}{b}^{\mathrm{2}} +\frac{{a}+\mathrm{4}}{{a}}{b}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{generally}\:\mathrm{solved} \\ $$$$ \\ $$$$\mathrm{with}\:{a}+{b}=\mathrm{1}\:\Rightarrow\:{b}=\mathrm{1}−{a}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{I}\right)\:\:\frac{{a}\left({a}−\mathrm{2}\right)\left({a}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{3}} +\mathrm{8}{a}^{\mathrm{2}} +\mathrm{6}{a}−\mathrm{6}\right)}{\left({a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{a}=\mathrm{0}\:\vee\:{a}=\mathrm{2}\:\mathrm{not}\:\mathrm{of}\:\mathrm{further}\:\mathrm{interest}\right] \\ $$$$\:\:\:\:\:\left[{a}^{\mathrm{2}} −\mathrm{4}{a}+\mathrm{1}\neq\mathrm{0}\:\Rightarrow\:{a}\neq\mathrm{2}−\sqrt{\mathrm{3}}\:\wedge\:{a}\neq\mathrm{2}+\sqrt{\mathrm{3}}\right] \\ $$$${a}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{3}} +\mathrm{8}{a}^{\mathrm{2}} +\mathrm{6}{a}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{again}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{exactly}\:\mathrm{solved}\:\mathrm{but}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{usual}\:\mathrm{difficulties},\:\mathrm{approximately}\:\mathrm{we}\:\mathrm{get} \\ $$$${a}\approx.\mathrm{669174} \\ $$$$\:\:\:\:\:\left[{a}\approx−.\mathrm{895728}\:\mathrm{not}\:\mathrm{of}\:\mathrm{further}\:\mathrm{interest}\right] \\ $$
Commented by ajfour last updated on 10/Jul/18
$${Thank}\:{you}\:{Sir}.\:{I}\:{was}\:{bit}\:{worried}. \\ $$
