Question-39649

Question Number 39649 by rahul 19 last updated on 09/Jul/18

Commented by rahul 19 last updated on 09/Jul/18

Given mass of block A & C = m mass of block B = 2m. Spring constant = k. Find acc^n of the blocks A,B & C at the instant when the string between B&C is cut?

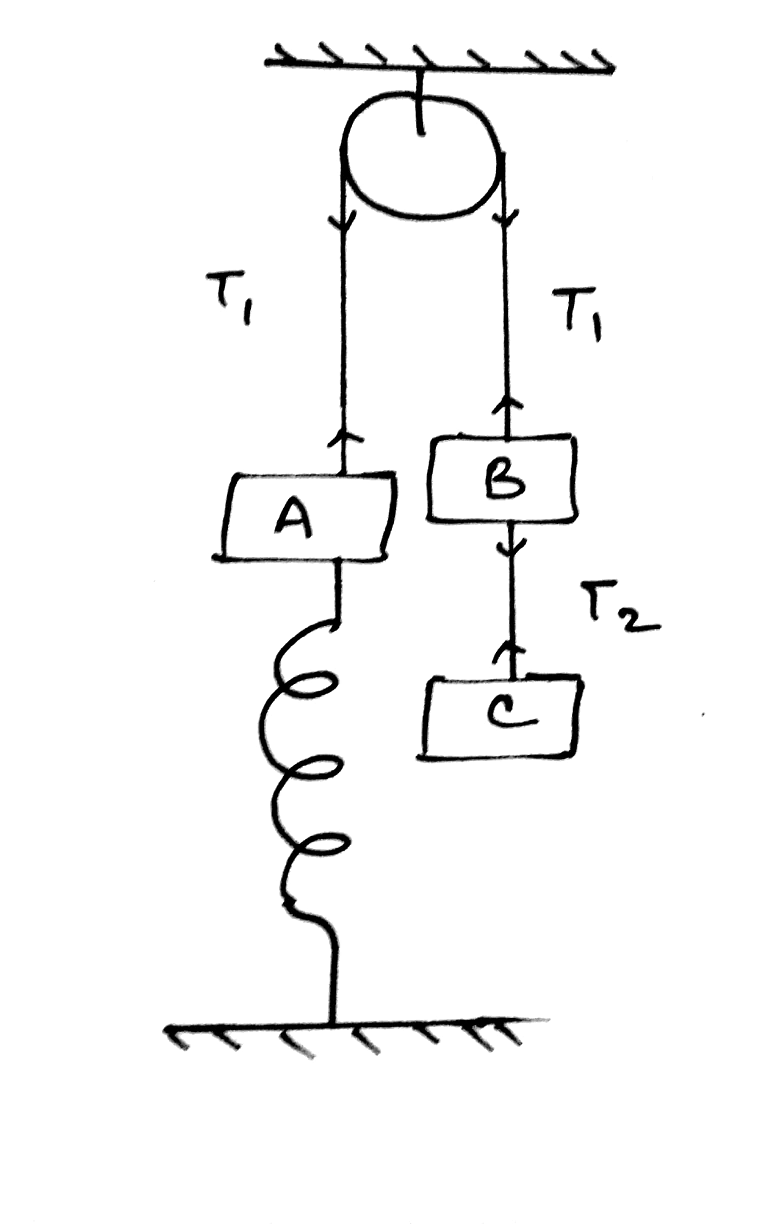
$$\mathrm{Given}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{block}\:\mathrm{A}\:\&\:\mathrm{C}\:=\:\mathrm{m} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{mass}\:\mathrm{of}\:\mathrm{block}\:\mathrm{B}\:=\:\mathrm{2m}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Spring}\:\mathrm{constant}\:=\:\mathrm{k}. \\ $$$$\mathrm{Find}\:\mathrm{acc}^{\mathrm{n}} \:\mathrm{of}\:\mathrm{the}\:\mathrm{blocks}\:\mathrm{A},\mathrm{B}\:\&\:\mathrm{C}\:\mathrm{at}\:\mathrm{the} \\ $$$$\mathrm{instant}\:\mathrm{when}\:\mathrm{the}\:\mathrm{string}\:\mathrm{between}\:\mathrm{B\&C} \\ $$$$\mathrm{is}\:\mathrm{cut}? \\ $$

Answered by MrW3 last updated on 09/Jul/18

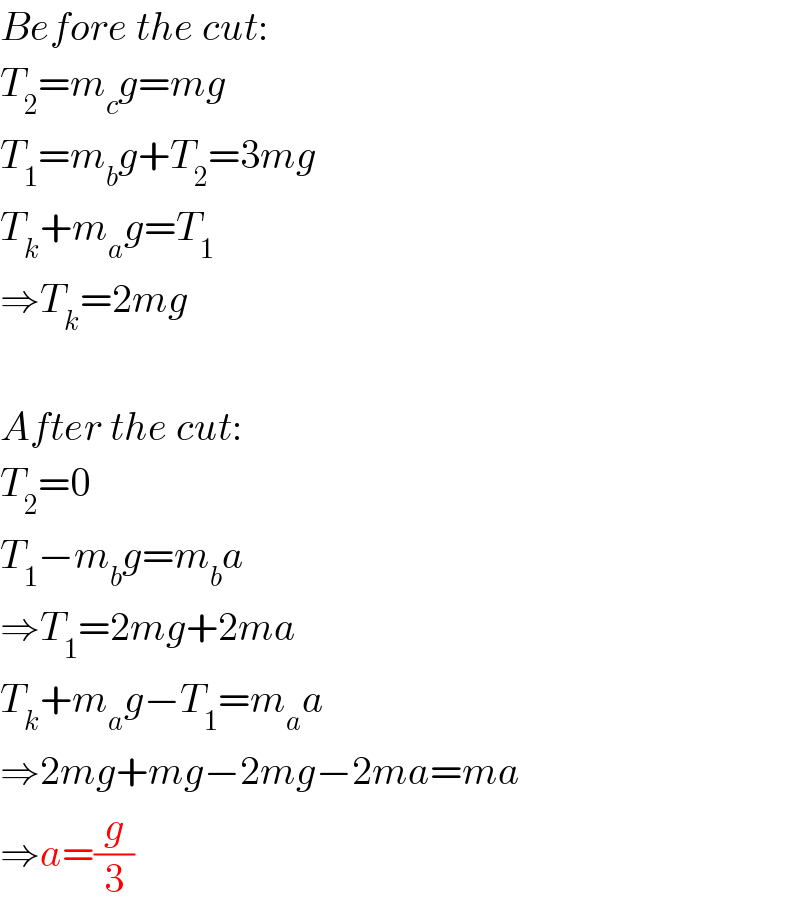
Before the cut: T_2 =m_c g=mg T_1 =m_b g+T_2 =3mg T_k +m_a g=T_1 ⇒T_k =2mg After the cut: T_2 =0 T_1 −m_b g=m_b a ⇒T_1 =2mg+2ma T_k +m_a g−T_1 =m_a a ⇒2mg+mg−2mg−2ma=ma ⇒a=(g/3)

$${Before}\:{the}\:{cut}: \\ $$$${T}_{\mathrm{2}} ={m}_{{c}} {g}={mg} \\ $$$${T}_{\mathrm{1}} ={m}_{{b}} {g}+{T}_{\mathrm{2}} =\mathrm{3}{mg} \\ $$$${T}_{{k}} +{m}_{{a}} {g}={T}_{\mathrm{1}} \\ $$$$\Rightarrow{T}_{{k}} =\mathrm{2}{mg} \\ $$$$ \\ $$$${After}\:{the}\:{cut}: \\ $$$${T}_{\mathrm{2}} =\mathrm{0} \\ $$$${T}_{\mathrm{1}} −{m}_{{b}} {g}={m}_{{b}} {a} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\mathrm{2}{mg}+\mathrm{2}{ma} \\ $$$${T}_{{k}} +{m}_{{a}} {g}−{T}_{\mathrm{1}} ={m}_{{a}} {a} \\ $$$$\Rightarrow\mathrm{2}{mg}+{mg}−\mathrm{2}{mg}−\mathrm{2}{ma}={ma} \\ $$$$\Rightarrow{a}=\frac{{g}}{\mathrm{3}} \\ $$

Commented by rahul 19 last updated on 09/Jul/18

Sir, i want to know why after the cut, T_1 and T_k remains same ? Why not after the cut new tension develops?

$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{why}\:\mathrm{after}\:\mathrm{the}\:\mathrm{cut}, \\ $$$$\mathrm{T}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{T}_{\mathrm{k}} \:\mathrm{remains}\:\mathrm{same}\:?\:\mathrm{Why}\:\mathrm{not} \\ $$$$\mathrm{after}\:\mathrm{the}\:\mathrm{cut}\:\mathrm{new}\:\mathrm{tension}\:\mathrm{develops}? \\ $$

Commented by ajfour last updated on 09/Jul/18

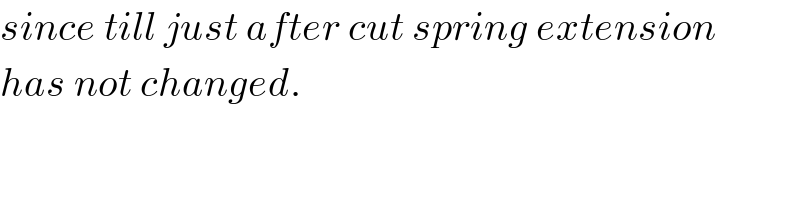
$${since}\:{till}\:{just}\:{after}\:{cut}\:{spring}\:{extension} \\ $$$${has}\:{not}\:{changed}. \\ $$

Commented by rahul 19 last updated on 09/Jul/18

Thank you sir !��

Commented by MrW3 last updated on 09/Jul/18

$${forces}\:{in}\:{strings}\:{and}\:{in}\:{springs} \\ $$$${will}\:{change}\:{when}\:{their}\:{deformation} \\ $$$${changes}\:{or}\:{when}\:{the}\:{acceleration}\:{of} \\ $$$${object}\:\:{changes}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply