Question-39678

Question Number 39678 by ajfour last updated on 09/Jul/18

Commented by ajfour last updated on 09/Jul/18

△ABC is projection of an equilateral △APQ. Find the height p,q of vertices P and Q above ground in terms of a,b,c.

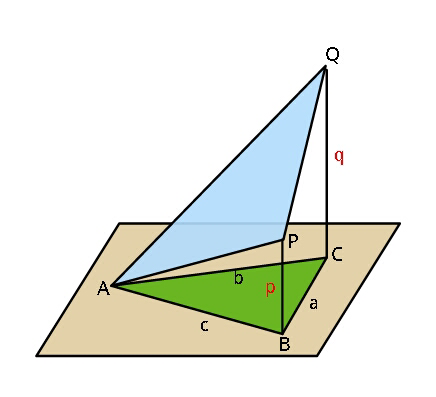
$$\bigtriangleup{ABC}\:{is}\:{projection}\:{of}\:{an}\: \\ $$$${equilateral}\:\bigtriangleup{APQ}.\:{Find}\:{the}\: \\ $$$${height}\:{p},{q}\:{of}\:{vertices}\:{P}\:{and}\:{Q} \\ $$$${above}\:{ground}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}. \\ $$

Answered by MrW3 last updated on 09/Jul/18

AP^2 =c^2 +p^2 AQ^2 =b^2 +q^2 PQ^2 =a^2 +(q−p)^2 since AP=AQ=PQ, b^2 +q^2 =a^2 +(q−p)^2 ...(i) ⇒b^2 =a^2 +p^2 −2pq ⇒q=((a^2 −b^2 +p^2 )/(2p)) p^2 −q^2 =b^2 −c^2 ...(ii) p^2 −(((a^2 −b^2 )^2 +p^4 +2(a^2 −b^2 )p^2 )/(4p^2 ))=b^2 −c^2 3p^4 −2(a^2 +b^2 −2c^2 )p^2 −(a^2 −b^2 )^2 =0 ⇒p^2 =(((a^2 +b^2 −2c^2 )+(√((a^2 +b^2 −2c^2 )^2 +3(a^2 −b^2 )^2 )))/3) ⇒p=(√(((a^2 +b^2 −2c^2 )+(√((a^2 +b^2 −2c^2 )^2 +3(a^2 −b^2 )^2 )))/3)) ⇒q=(√(((a^2 +c^2 −2b^2 )+(√((a^2 +c^2 −2b^2 )^2 +3(a^2 −c^2 )^2 )))/3))

$${AP}^{\mathrm{2}} ={c}^{\mathrm{2}} +{p}^{\mathrm{2}} \\ $$$${AQ}^{\mathrm{2}} ={b}^{\mathrm{2}} +{q}^{\mathrm{2}} \\ $$$${PQ}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({q}−{p}\right)^{\mathrm{2}} \\ $$$${since}\:{AP}={AQ}={PQ}, \\ $$$${b}^{\mathrm{2}} +{q}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({q}−{p}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\Rightarrow{b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{2}{pq} \\ $$$$\Rightarrow{q}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{p}^{\mathrm{2}} }{\mathrm{2}{p}} \\ $$$${p}^{\mathrm{2}} −{q}^{\mathrm{2}} ={b}^{\mathrm{2}} −{c}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$${p}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +{p}^{\mathrm{4}} +\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){p}^{\mathrm{2}} }{\mathrm{4}{p}^{\mathrm{2}} }={b}^{\mathrm{2}} −{c}^{\mathrm{2}} \\ $$$$\mathrm{3}{p}^{\mathrm{4}} −\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} \right){p}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} \right)+\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{3}} \\ $$$$\Rightarrow{p}=\sqrt{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} \right)+\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{3}}} \\ $$$$\Rightarrow{q}=\sqrt{\frac{\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right)+\sqrt{\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{3}}} \\ $$

Commented by MrW3 last updated on 10/Jul/18

$${This}\:{is}\:{to}\:{say}\:{every}\:{triangle}\:{can}\:{be} \\ $$$${projected}\:{from}\:{an}\:{equilateral}\:{triangle}. \\ $$

Commented by ajfour last updated on 10/Jul/18

$${Very}\:{nicely}\:{handled}\:{Sir},\:{cannot} \\ $$$${be}\:{better}!\:{Thanks}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply