Question Number 39709 by Raj Singh last updated on 10/Jul/18

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jul/18
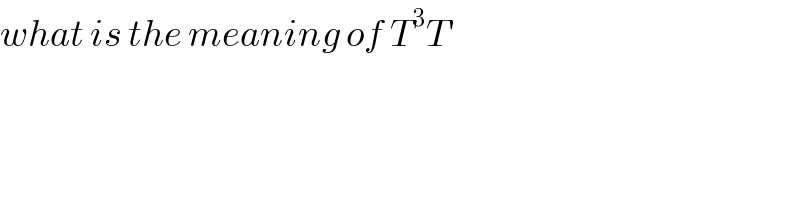
$${what}\:{is}\:{the}\:{meaning}\:{of}\:{T}^{\mathrm{3}} {T}'\:\:\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Jul/18

$${let}\:{point}\:{T}\:{is}\:{ct},\frac{{c}}{{t}} \\ $$$${eqn}\:{of}\:{normal}\:\:\left({y}−\frac{{c}}{{t}}\right)=\left(−\frac{\mathrm{1}}{{m}}\right)\left({x}−{ct}\right) \\ $$$${x}\frac{{dy}}{{dx}}+{y}=\mathrm{0}\:\:\:{so}\:\frac{{dy}}{{dx}}=\frac{−{y}}{{x}\:}\:\:{hence}\:\:{m}=\frac{−\frac{{c}}{{t}}}{{ct}} \\ $$$${m}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }\:\:\:\:\:{so}\:\:\frac{−\mathrm{1}}{{m}}={t}^{\mathrm{2}} \\ $$$${so}\:{normal}\:{eqn}\:\:\left({y}−\frac{{c}}{{t}}\right)=\left({t}^{\mathrm{2}} \right)\left({x}−{ct}\right) \\ $$$${now}\:{let}\:{T}'=\left({ct}_{\mathrm{1}} ,\frac{{c}}{{t}_{\mathrm{1}} }\right) \\ $$$$\left(\frac{{c}}{{t}_{\mathrm{1}} }−\frac{{c}}{{t}}\right)={t}^{\mathrm{2}} \left({ct}_{\mathrm{1}} −{ct}\right) \\ $$$$\left(\frac{{ct}−{ct}_{\mathrm{1}} }{{tt}_{\mathrm{1}} }\right)−{t}^{\mathrm{2}} \left({ct}_{\mathrm{1}} −{ct}\right)=\mathrm{0}\:{ihave}\:{done}\:{some}\:{mistske} \\ $$$${edited} \\ $$$$ \\ $$$$\left({ct}−{ct}_{\mathrm{1}} \right)\left(\frac{\mathrm{1}}{{tt}_{\mathrm{1}} }+{t}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${t}^{\mathrm{3}} {t}_{\mathrm{1}} +\mathrm{1}=\mathrm{0}\:\:\:\:\:\:{so}\:\:{t}^{\mathrm{3}} {t}_{\mathrm{1}} =−\mathrm{1} \\ $$$${point}\:{T}\left({ct},\frac{{c}}{{t}}\right)\:\:{and}\:{point}\:{T}'\left(\frac{{c}}{−{t}^{\mathrm{3}} },\frac{−{ct}^{\mathrm{3}} }{}\right) \\ $$
Commented by Raj Singh last updated on 10/Jul/18

$${how}\:{you}\:{find}\:\left({ct},{c}/{t}\right) \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jul/18

$${ct},\frac{{c}}{{t}}\:\:{is}\:{a}\:{point}\:{lies}\:{on}\:{the}\:{curve}…{parsmetric} \\ $$
