Question Number 39811 by ajfour last updated on 11/Jul/18

Commented by ajfour last updated on 11/Jul/18

$${The}\:{outer}\:{frame}\:{is}\:{a}\:{unit}\:{square}. \\ $$$${Find}\:{areas}\:{of}\:{red},\:{green},\:{and} \\ $$$${blue}\:{regions}\:{in}\:{terms}\:{of}\:\alpha. \\ $$
Answered by MrW3 last updated on 11/Jul/18
![tan β=((1−1×tan α)/1)=1−tan α ⇒β=tan^(−1) (1−tan α) ⇒sin β=((1−tan α)/( (√(1+(1−tan α)^2 )))) ⇒cos β=(1/( (√(1+(1−tan α)^2 )))) side length of blue square: 1×tan α×cos β=((tan α)/( (√(1+(1−tan α)^2 )))) ⇒A_(Blue) =((tan^2 α)/(1+(1−tan α)^2 )) Red triangle: side a=1×sin α side b with (b/(sin α))=(1/(sin (α+β))) ⇒b=((1×sin α)/(sin (α+β)))=((sin α (√(1+(1−tan α)^2 )))/(sin α +cos α (1−tan α)))=tan α (√(1+(1−tan α)^2 )) ⇒A_(Red) =(1/2)×sin α×tan α (√(1+(1−tan α)^2 ))×cos (α+β) (1/2)×sin α×tan α×[cos α−sin α (1−tan α)] ⇒A_(Red) =(((2−sin 2α) tan^2 α)/4) Green triangle: side c with c=1×sin β−b=((1−tan α)/( (√(1+(1−tan α)^2 ))))−tan α (√(1+(1−tan α)^2 )) =((1−tan α−tan α [1+(1−tan α)^2 ])/( (√(1+(1−tan α)^2 )))) =((1−2tan α−tan α(1−tan α)^2 )/( (√(1+(1−tan α)^2 )))) side d with d=c tan γ=c tan (α+β)=c ((tan α+(1−tan α))/(1−tan α(1−tan α))) =((1−2tan α−tan α(1−tan α)^2 )/((1−tan α+tan^2 α)(√(1+(1−tan α)^2 )))) A_(Green) =((cd)/2)=(1/2)×((1−tan α−tan α [1+(1−tan α)^2 ])/( (√(1+(1−tan α)^2 ))))×((1−2tan α−tan α(1−tan α)^2 )/((1−tan α+tan^2 α)(√(1+(1−tan α)^2 )))) ⇒A_(Green) =(([1−2tan α−tan α(1−tan α)^2 ]^2 )/(2(1−tan α+tan^2 α)[1+(1−tan α)^2 ]))](https://www.tinkutara.com/question/Q39830.png)
$$\mathrm{tan}\:\beta=\frac{\mathrm{1}−\mathrm{1}×\mathrm{tan}\:\alpha}{\mathrm{1}}=\mathrm{1}−\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\beta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{tan}\:\alpha\right) \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{1}−\mathrm{tan}\:\alpha}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$${side}\:{length}\:{of}\:{blue}\:{square}: \\ $$$$\mathrm{1}×\mathrm{tan}\:\alpha×\mathrm{cos}\:\beta=\frac{\mathrm{tan}\:\alpha}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{\mathrm{tan}^{\mathrm{2}} \:\alpha}{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${Red}\:{triangle}: \\ $$$${side}\:{a}=\mathrm{1}×\mathrm{sin}\:\alpha \\ $$$${side}\:{b}\:{with} \\ $$$$\frac{{b}}{\mathrm{sin}\:\alpha}=\frac{\mathrm{1}}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}×\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{\mathrm{sin}\:\alpha\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }}{\mathrm{sin}\:\alpha\:+\mathrm{cos}\:\alpha\:\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)}=\mathrm{tan}\:\alpha\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{A}_{{Red}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{sin}\:\alpha×\mathrm{tan}\:\alpha\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }×\mathrm{cos}\:\left(\alpha+\beta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{sin}\:\alpha×\mathrm{tan}\:\alpha×\left[\mathrm{cos}\:\alpha−\mathrm{sin}\:\alpha\:\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)\right] \\ $$$$\Rightarrow{A}_{{Red}} =\frac{\left(\mathrm{2}−\mathrm{sin}\:\mathrm{2}\alpha\right)\:\mathrm{tan}^{\mathrm{2}} \:\alpha}{\mathrm{4}} \\ $$$$ \\ $$$${Green}\:{triangle}: \\ $$$${side}\:{c}\:{with} \\ $$$${c}=\mathrm{1}×\mathrm{sin}\:\beta−{b}=\frac{\mathrm{1}−\mathrm{tan}\:\alpha}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }}−\mathrm{tan}\:\alpha\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{tan}\:\alpha−\mathrm{tan}\:\alpha\:\left[\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} \right]}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}−\mathrm{2tan}\:\alpha−\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$${side}\:{d}\:{with} \\ $$$${d}={c}\:\mathrm{tan}\:\gamma={c}\:\mathrm{tan}\:\left(\alpha+\beta\right)={c}\:\frac{\mathrm{tan}\:\alpha+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)}{\mathrm{1}−\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)} \\ $$$$=\frac{\mathrm{1}−\mathrm{2tan}\:\alpha−\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{tan}\:\alpha+\mathrm{tan}^{\mathrm{2}} \:\alpha\right)\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$${A}_{{Green}} =\frac{{cd}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}−\mathrm{tan}\:\alpha−\mathrm{tan}\:\alpha\:\left[\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} \right]}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }}×\frac{\mathrm{1}−\mathrm{2tan}\:\alpha−\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{tan}\:\alpha+\mathrm{tan}^{\mathrm{2}} \:\alpha\right)\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{A}_{{Green}} =\frac{\left[\mathrm{1}−\mathrm{2tan}\:\alpha−\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} \right]^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{tan}\:\alpha+\mathrm{tan}^{\mathrm{2}} \:\alpha\right)\left[\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)^{\mathrm{2}} \right]} \\ $$
Commented by MrW3 last updated on 11/Jul/18
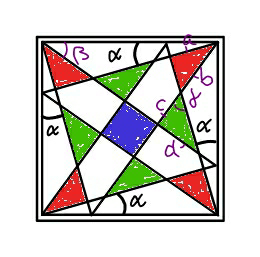
Commented by ajfour last updated on 12/Jul/18

$${Great}!\:\left({patience}\:{and}\:{idea}\:{both}\right),{Sir} \\ $$$$\:{Thank}\:{you}.\:{I}\:{will}\:{also}\:{try}.\: \\ $$
