Question-39851

Question Number 39851 by Raj Singh last updated on 12/Jul/18

Commented by MrW3 last updated on 12/Jul/18

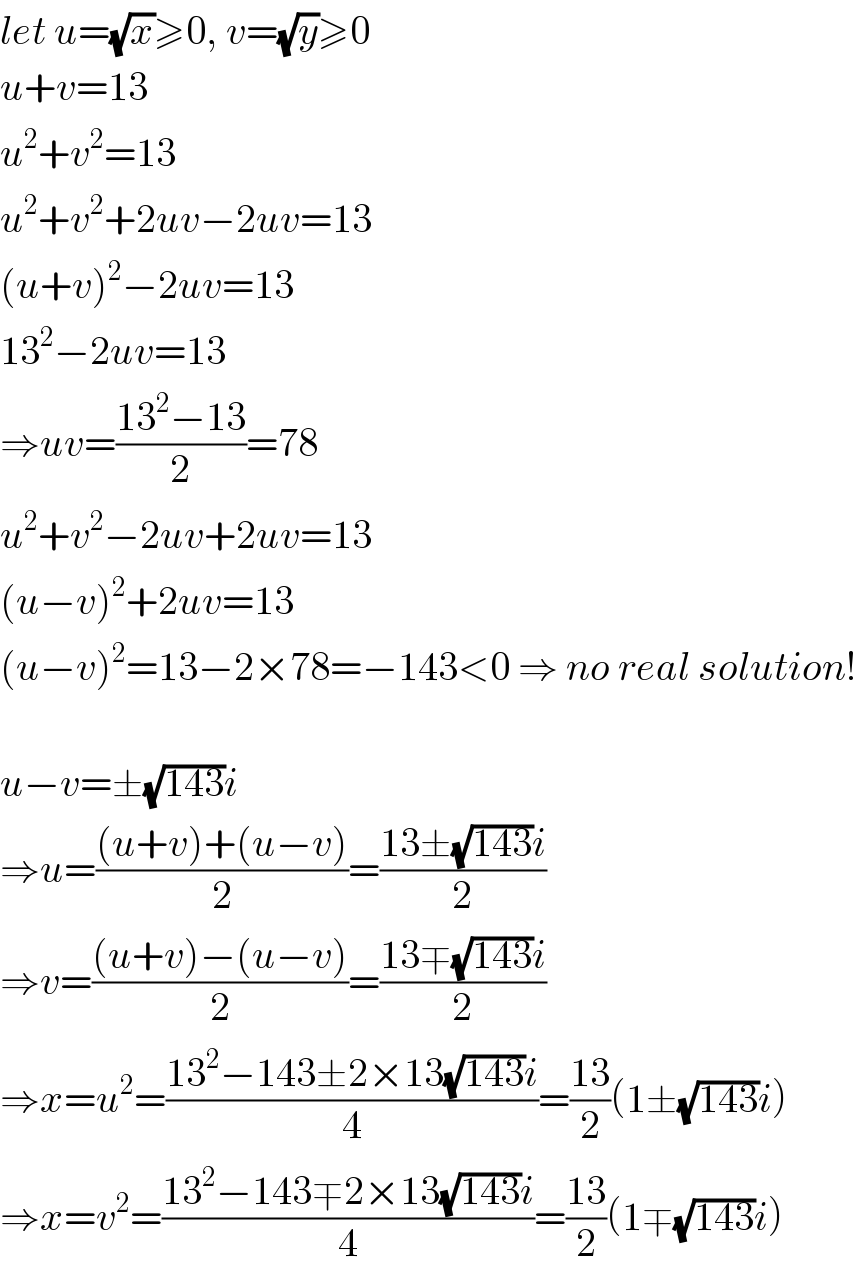
let u=(√x)≥0, v=(√y)≥0 u+v=13 u^2 +v^2 =13 u^2 +v^2 +2uv−2uv=13 (u+v)^2 −2uv=13 13^2 −2uv=13 ⇒uv=((13^2 −13)/2)=78 u^2 +v^2 −2uv+2uv=13 (u−v)^2 +2uv=13 (u−v)^2 =13−2×78=−143<0 ⇒ no real solution! u−v=±(√(143))i ⇒u=(((u+v)+(u−v))/2)=((13±(√(143))i)/2) ⇒v=(((u+v)−(u−v))/2)=((13∓(√(143))i)/2) ⇒x=u^2 =((13^2 −143±2×13(√(143))i)/4)=((13)/2)(1±(√(143))i) ⇒x=v^2 =((13^2 −143∓2×13(√(143))i)/4)=((13)/2)(1∓(√(143))i)

$${let}\:{u}=\sqrt{{x}}\geqslant\mathrm{0},\:{v}=\sqrt{{y}}\geqslant\mathrm{0} \\ $$$${u}+{v}=\mathrm{13} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{13} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} +\mathrm{2}{uv}−\mathrm{2}{uv}=\mathrm{13} \\ $$$$\left({u}+{v}\right)^{\mathrm{2}} −\mathrm{2}{uv}=\mathrm{13} \\ $$$$\mathrm{13}^{\mathrm{2}} −\mathrm{2}{uv}=\mathrm{13} \\ $$$$\Rightarrow{uv}=\frac{\mathrm{13}^{\mathrm{2}} −\mathrm{13}}{\mathrm{2}}=\mathrm{78} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} −\mathrm{2}{uv}+\mathrm{2}{uv}=\mathrm{13} \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} +\mathrm{2}{uv}=\mathrm{13} \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} =\mathrm{13}−\mathrm{2}×\mathrm{78}=−\mathrm{143}<\mathrm{0}\:\Rightarrow\:{no}\:{real}\:{solution}! \\ $$$$ \\ $$$${u}−{v}=\pm\sqrt{\mathrm{143}}{i} \\ $$$$\Rightarrow{u}=\frac{\left({u}+{v}\right)+\left({u}−{v}\right)}{\mathrm{2}}=\frac{\mathrm{13}\pm\sqrt{\mathrm{143}}{i}}{\mathrm{2}} \\ $$$$\Rightarrow{v}=\frac{\left({u}+{v}\right)−\left({u}−{v}\right)}{\mathrm{2}}=\frac{\mathrm{13}\mp\sqrt{\mathrm{143}}{i}}{\mathrm{2}} \\ $$$$\Rightarrow{x}={u}^{\mathrm{2}} =\frac{\mathrm{13}^{\mathrm{2}} −\mathrm{143}\pm\mathrm{2}×\mathrm{13}\sqrt{\mathrm{143}}{i}}{\mathrm{4}}=\frac{\mathrm{13}}{\mathrm{2}}\left(\mathrm{1}\pm\sqrt{\mathrm{143}}{i}\right) \\ $$$$\Rightarrow{x}={v}^{\mathrm{2}} =\frac{\mathrm{13}^{\mathrm{2}} −\mathrm{143}\mp\mathrm{2}×\mathrm{13}\sqrt{\mathrm{143}}{i}}{\mathrm{4}}=\frac{\mathrm{13}}{\mathrm{2}}\left(\mathrm{1}\mp\sqrt{\mathrm{143}}{i}\right) \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 12/Jul/18

(√x) +(√(13−x)) =13 x+13−x+2(√(13x−x^2 )) =169 (√(13x−x^2 )) =78 13x−x^2 =6084 x^2 −13x+6084=0 x=((−b±(√(b^2 −4ac)))/(2a)) x=((13±(√(169−4×6084)) )/2) =((13±(√(−24267)) )/2)=((13±i(√(24167)))/2) x=((13+i(√(24167)))/2) y= ((13−i(√(24167)))/2) x=((13−i(√(24167)))/2) y=((13+i(√(24267)))/2)

$$\sqrt{{x}}\:+\sqrt{\mathrm{13}−{x}}\:=\mathrm{13} \\ $$$${x}+\mathrm{13}−{x}+\mathrm{2}\sqrt{\mathrm{13}{x}−{x}^{\mathrm{2}} \:}\:=\mathrm{169} \\ $$$$\sqrt{\mathrm{13}{x}−{x}^{\mathrm{2}} }\:=\mathrm{78} \\ $$$$\mathrm{13}{x}−{x}^{\mathrm{2}} =\mathrm{6084} \\ $$$${x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{6084}=\mathrm{0} \\ $$$${x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$${x}=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{4}×\mathrm{6084}}\:}{\mathrm{2}} \\ $$$$ \\ $$$$=\frac{\mathrm{13}\pm\sqrt{−\mathrm{24267}}\:}{\mathrm{2}}=\frac{\mathrm{13}\pm{i}\sqrt{\mathrm{24167}}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{13}+{i}\sqrt{\mathrm{24167}}}{\mathrm{2}}\:\:\:{y}=\:\frac{\mathrm{13}−{i}\sqrt{\mathrm{24167}}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{13}−{i}\sqrt{\mathrm{24167}}}{\mathrm{2}}\:\:{y}=\frac{\mathrm{13}+{i}\sqrt{\mathrm{24267}}}{\mathrm{2}} \\ $$

Answered by MJS last updated on 12/Jul/18

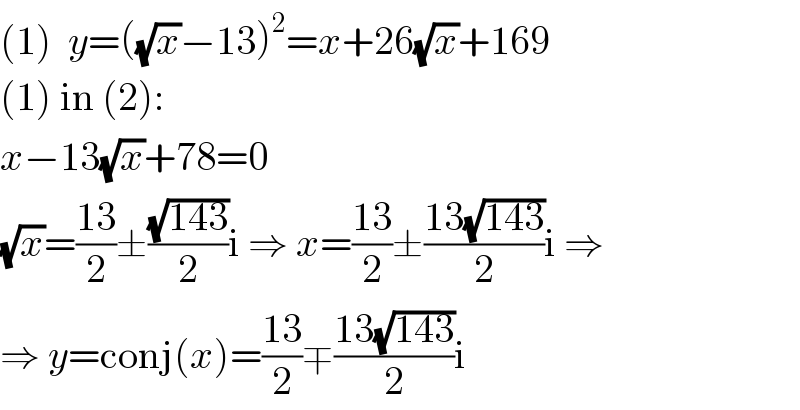
(1) y=((√x)−13)^2 =x+26(√x)+169 (1) in (2): x−13(√x)+78=0 (√x)=((13)/2)±((√(143))/2)i ⇒ x=((13)/2)±((13(√(143)))/2)i ⇒ ⇒ y=conj(x)=((13)/2)∓((13(√(143)))/2)i

$$\left(\mathrm{1}\right)\:\:{y}=\left(\sqrt{{x}}−\mathrm{13}\right)^{\mathrm{2}} ={x}+\mathrm{26}\sqrt{{x}}+\mathrm{169} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{in}\:\left(\mathrm{2}\right): \\ $$$${x}−\mathrm{13}\sqrt{{x}}+\mathrm{78}=\mathrm{0} \\ $$$$\sqrt{{x}}=\frac{\mathrm{13}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{143}}}{\mathrm{2}}\mathrm{i}\:\Rightarrow\:{x}=\frac{\mathrm{13}}{\mathrm{2}}\pm\frac{\mathrm{13}\sqrt{\mathrm{143}}}{\mathrm{2}}\mathrm{i}\:\Rightarrow \\ $$$$\Rightarrow\:{y}=\mathrm{conj}\left({x}\right)=\frac{\mathrm{13}}{\mathrm{2}}\mp\frac{\mathrm{13}\sqrt{\mathrm{143}}}{\mathrm{2}}\mathrm{i} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply