Menu Close

Question-39854

Tinku Tara 0 Comments
Pin




Question Number 39854 by ajfour last updated on 12/Jul/18
Commented by ajfour last updated on 12/Jul/18
Choose the correct options: (i) a≈1.6 (ii) b≈2.7 (iii) a ≈ 1.8 (iv) b ≈ 2.4
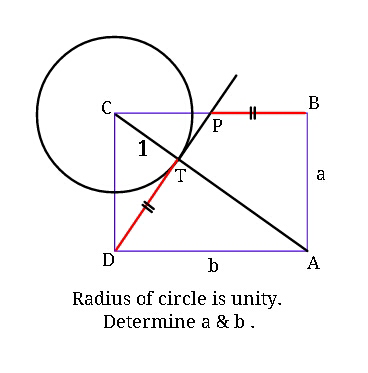
$${Choose}\:{the}\:{correct}\:{options}: \\ $$$$\left({i}\right)\:{a}\approx\mathrm{1}.\mathrm{6}\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:\:{b}\approx\mathrm{2}.\mathrm{7} \\ $$$$\left({iii}\right)\:\:{a}\:\approx\:\mathrm{1}.\mathrm{8}\:\:\:\left({iv}\right)\:\:{b}\:\approx\:\mathrm{2}.\mathrm{4} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Jul/18
every problem you post really praiseworthy you please repost those probems remain unsolved till dateso that we get option . to choose..
$${every}\:{problem}\:{you}\:{post}\:{really}\:{praiseworthy} \\ $$$${you}\:{please}\:{repost}\:{those}\:{probems}\:{remain} \\ $$$${unsolved}\:{till}\:{dateso}\:{that}\:{we}\:{get}\:{option}\:. \\ $$$${to}\:{choose}.. \\ $$$$ \\ $$
Answered by MrW3 last updated on 12/Jul/18
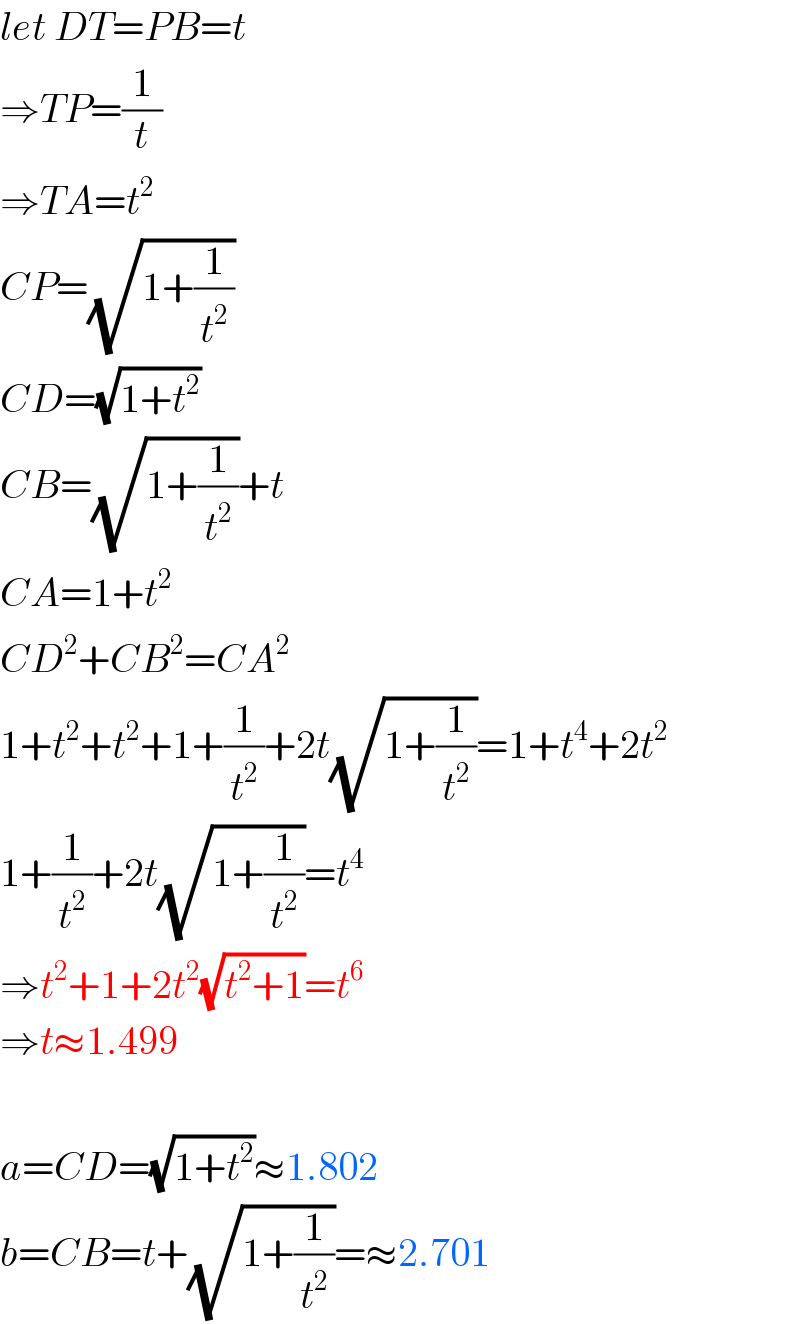
let DT=PB=t ⇒TP=(1/t) ⇒TA=t^2 CP=(√(1+(1/t^2 ))) CD=(√(1+t^2 )) CB=(√(1+(1/t^2 )))+t CA=1+t^2 CD^2 +CB^2 =CA^2 1+t^2 +t^2 +1+(1/t^2 )+2t(√(1+(1/t^2 )))=1+t^4 +2t^2 1+(1/t^2 )+2t(√(1+(1/t^2 )))=t^4 ⇒t^2 +1+2t^2 (√(t^2 +1))=t^6 ⇒t≈1.499 a=CD=(√(1+t^2 ))≈1.802 b=CB=t+(√(1+(1/t^2 )))=≈2.701
$${let}\:{DT}={PB}={t} \\ $$$$\Rightarrow{TP}=\frac{\mathrm{1}}{{t}} \\ $$$$\Rightarrow{TA}={t}^{\mathrm{2}} \\ $$$${CP}=\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }} \\ $$$${CD}=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${CB}=\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}+{t} \\ $$$${CA}=\mathrm{1}+{t}^{\mathrm{2}} \\ $$$${CD}^{\mathrm{2}} +{CB}^{\mathrm{2}} ={CA}^{\mathrm{2}} \\ $$$$\mathrm{1}+{t}^{\mathrm{2}} +{t}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{2}{t}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}=\mathrm{1}+{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{2}{t}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}={t}^{\mathrm{4}} \\ $$$$\Rightarrow{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}}={t}^{\mathrm{6}} \\ $$$$\Rightarrow{t}\approx\mathrm{1}.\mathrm{499} \\ $$$$ \\ $$$${a}={CD}=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\approx\mathrm{1}.\mathrm{802} \\ $$$${b}={CB}={t}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}=\approx\mathrm{2}.\mathrm{701} \\ $$
Commented by ajfour last updated on 12/Jul/18
Alright Sir, thanks ′gain.
$${Alright}\:{Sir},\:{thanks}\:'{gain}. \\ $$
Answered by ajfour last updated on 12/Jul/18
Let ∠CDP = ∠ACB = θ As DT = BP ⇒ acos θ = (a/(tan θ))−atan θ ⇒ sin θcos^2 θ = cos^2 θ−sin^2 θ let sin θ = x ⇒ x(1−x^2 )=1−2x^2 ⇒ x^3 −2x^2 −x+1=0 _________________________ let x= t+(2/3) ⇒ t^3 +2t^2 +((4t)/3)+(8/(27))−2t^2 −((8t)/3)−((24)/(27)) −((3t)/3)−((18)/(27))+((27)/(27)) =0 ⇒ t^3 −((7t)/3)−(7/(27))=0 let t= u+v ⇒ u^3 +v^3 +(u+v)(3uv−(7/3))=(7/(27)) let uv = (7/9) ⇒ u^3 v^3 = ((343)/(729)) and u^3 +v^3 =(7/(27)) u^3 and v^3 are then roots of z^2 −((7z)/(27))+((343)/(729)) =0 z = (((7/(27))±(√(((49)/(27×27))−((1372)/(729)))))/2) t= u+v (appropriate value < 0 ) t=(((7+i(√(1323)))/(54)))^(1/3) +(((7−i(√(1323)))/(54)))^(1/3) let t= r^(1/3) (cos θ+isin θ)^(1/3) +r^(1/3) (cos θ−isin θ)^(1/3) where r= ((√(49+1323))/(54)) =((√(1372))/(54)) rcos θ = (7/(54)) ⇒ cos (2π−θ) = (7/( (√(1372)))) ⇒ x =t+(2/3)= 2r^(1/3) cos (θ/3)+(2/3) x = 2(((√(1372))/(54)))^(1/3) cos (((2π)/3)−(1/3)cos^(−1) (7/( (√(1372)))))+(2/3) _________________________ ⇒ x≈ 0.55496 a= (1/(sin 𝛉)) =(1/x) ≈ 1.802 b=acot 𝛉 = a(√((1/(sin^2 𝛉))−1)) ≈ 1.802×(√((1/((0.55496)^2 ))−1)) ⇒ b ≈ 2.701 .
$${Let}\:\:\angle{CDP}\:=\:\angle{ACB}\:=\:\theta \\ $$$${As}\:\:\:\:\boldsymbol{{DT}}\:=\:\boldsymbol{{BP}} \\ $$$$\Rightarrow\:\:\:{a}\mathrm{cos}\:\theta\:=\:\frac{{a}}{\mathrm{tan}\:\theta}−{a}\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\theta\mathrm{cos}\:^{\mathrm{2}} \theta\:=\:\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${let}\:\mathrm{sin}\:\theta\:=\:{x} \\ $$$$\Rightarrow\:\:\:{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\boldsymbol{{x}}^{\mathrm{3}} −\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${let}\:{x}=\:{t}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} +\frac{\mathrm{4}{t}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{27}}−\mathrm{2}{t}^{\mathrm{2}} −\frac{\mathrm{8}{t}}{\mathrm{3}}−\frac{\mathrm{24}}{\mathrm{27}} \\ $$$$\:\:\:\:\:\:\:−\frac{\mathrm{3}{t}}{\mathrm{3}}−\frac{\mathrm{18}}{\mathrm{27}}+\frac{\mathrm{27}}{\mathrm{27}}\:=\mathrm{0} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} −\frac{\mathrm{7}{t}}{\mathrm{3}}−\frac{\mathrm{7}}{\mathrm{27}}=\mathrm{0} \\ $$$${let}\:\:{t}=\:{u}+{v} \\ $$$$\Rightarrow\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} +\left({u}+{v}\right)\left(\mathrm{3}{uv}−\frac{\mathrm{7}}{\mathrm{3}}\right)=\frac{\mathrm{7}}{\mathrm{27}} \\ $$$${let}\:\:\:{uv}\:=\:\frac{\mathrm{7}}{\mathrm{9}}\:\:\Rightarrow\:\:{u}^{\mathrm{3}} {v}^{\mathrm{3}} \:=\:\frac{\mathrm{343}}{\mathrm{729}} \\ $$$${and}\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} =\frac{\mathrm{7}}{\mathrm{27}} \\ $$$${u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \:{are}\:{then}\:{roots}\:{of} \\ $$$$\:\:\:\:\:\:{z}^{\mathrm{2}} −\frac{\mathrm{7}{z}}{\mathrm{27}}+\frac{\mathrm{343}}{\mathrm{729}}\:=\mathrm{0} \\ $$$$\:\:\:\:{z}\:=\:\frac{\frac{\mathrm{7}}{\mathrm{27}}\pm\sqrt{\frac{\mathrm{49}}{\mathrm{27}×\mathrm{27}}−\frac{\mathrm{1372}}{\mathrm{729}}}}{\mathrm{2}}\: \\ $$$$\:\:\:{t}=\:{u}+{v}\:\:\:\:\:\:\:\:\:\:\left({appropriate}\:{value}\:<\:\mathrm{0}\:\right) \\ $$$$\:{t}=\left(\frac{\mathrm{7}+{i}\sqrt{\mathrm{1323}}}{\mathrm{54}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{\mathrm{7}−{i}\sqrt{\mathrm{1323}}}{\mathrm{54}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${let}\:\:{t}=\:{r}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:+{r}^{\mathrm{1}/\mathrm{3}} \left(\mathrm{cos}\:\theta−{i}\mathrm{sin}\:\theta\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${where}\:\:\:{r}=\:\frac{\sqrt{\mathrm{49}+\mathrm{1323}}}{\mathrm{54}}\:=\frac{\sqrt{\mathrm{1372}}}{\mathrm{54}} \\ $$$$\:\:{r}\mathrm{cos}\:\theta\:=\:\frac{\mathrm{7}}{\mathrm{54}}\:\:\:\Rightarrow\:\mathrm{cos}\:\left(\mathrm{2}\pi−\theta\right)\:=\:\frac{\mathrm{7}}{\:\sqrt{\mathrm{1372}}} \\ $$$$\Rightarrow\:\:\:{x}\:={t}+\frac{\mathrm{2}}{\mathrm{3}}=\:\mathrm{2}{r}^{\mathrm{1}/\mathrm{3}} \mathrm{cos}\:\frac{\theta}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:\:\:\:\boldsymbol{{x}}\:=\:\mathrm{2}\left(\frac{\sqrt{\mathrm{1372}}}{\mathrm{54}}\right)^{\mathrm{1}/\mathrm{3}} \mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{7}}{\:\sqrt{\mathrm{1372}}}\right)+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\boldsymbol{{x}}\approx\:\mathrm{0}.\mathrm{55496} \\ $$$$\:\boldsymbol{{a}}=\:\frac{\mathrm{1}}{\mathrm{sin}\:\boldsymbol{\theta}}\:=\frac{\mathrm{1}}{{x}}\:\approx\:\mathrm{1}.\mathrm{802} \\ $$$$\:\boldsymbol{{b}}=\boldsymbol{{a}}\mathrm{cot}\:\boldsymbol{\theta}\:=\:\boldsymbol{{a}}\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \boldsymbol{\theta}}−\mathrm{1}} \\ $$$$\:\:\:\:\approx\:\mathrm{1}.\mathrm{802}×\sqrt{\frac{\mathrm{1}}{\left(\mathrm{0}.\mathrm{55496}\right)^{\mathrm{2}} }−\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\boldsymbol{{b}}\:\approx\:\mathrm{2}.\mathrm{701}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *