Menu Close

Question-39921

Tinku Tara 0 Comments
Pin




Question Number 39921 by Raj Singh last updated on 13/Jul/18
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
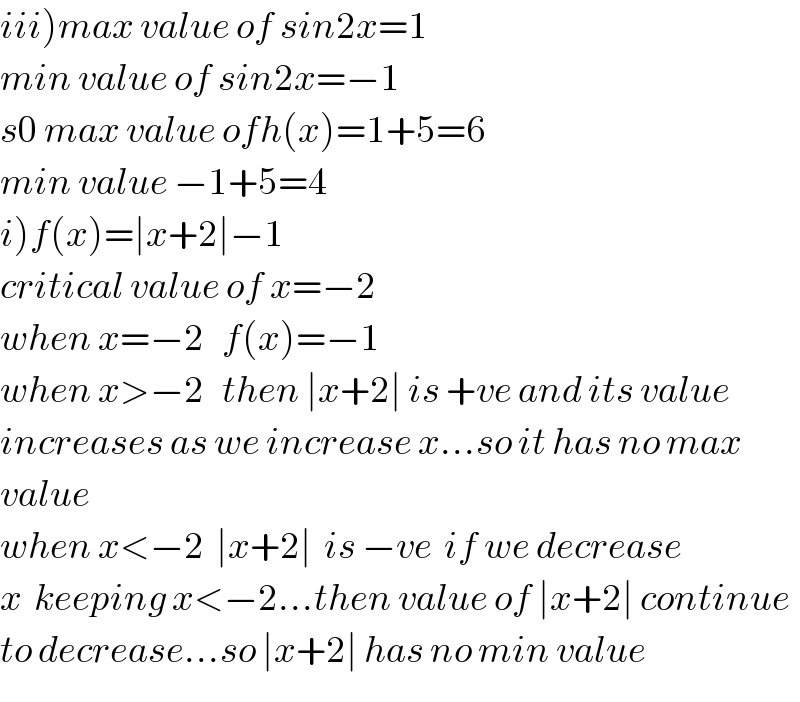
iii)max value of sin2x=1 min value of sin2x=−1 s0 max value ofh(x)=1+5=6 min value −1+5=4 i)f(x)=∣x+2∣−1 critical value of x=−2 when x=−2 f(x)=−1 when x>−2 then ∣x+2∣ is +ve and its value increases as we increase x...so it has no max value when x<−2 ∣x+2∣ is −ve if we decrease x keeping x<−2...then value of ∣x+2∣ continue to decrease...so ∣x+2∣ has no min value
$$\left.{iii}\right){max}\:{value}\:{of}\:{sin}\mathrm{2}{x}=\mathrm{1} \\ $$$${min}\:{value}\:{of}\:{sin}\mathrm{2}{x}=−\mathrm{1} \\ $$$${s}\mathrm{0}\:{max}\:{value}\:{ofh}\left({x}\right)=\mathrm{1}+\mathrm{5}=\mathrm{6} \\ $$$${min}\:{value}\:−\mathrm{1}+\mathrm{5}=\mathrm{4} \\ $$$$\left.{i}\right){f}\left({x}\right)=\mid{x}+\mathrm{2}\mid−\mathrm{1} \\ $$$${critical}\:{value}\:{of}\:{x}=−\mathrm{2} \\ $$$${when}\:{x}=−\mathrm{2}\:\:\:{f}\left({x}\right)=−\mathrm{1} \\ $$$${when}\:{x}>−\mathrm{2}\:\:\:{then}\:\mid{x}+\mathrm{2}\mid\:{is}\:+{ve}\:{and}\:{its}\:{value} \\ $$$${increases}\:{as}\:{we}\:{increase}\:{x}…{so}\:{it}\:{has}\:{no}\:{max} \\ $$$${value} \\ $$$${when}\:{x}<−\mathrm{2}\:\:\mid{x}+\mathrm{2}\mid\:\:{is}\:−{ve}\:\:{if}\:{we}\:{decrease} \\ $$$${x}\:\:{keeping}\:{x}<−\mathrm{2}…{then}\:{value}\:{of}\:\mid{x}+\mathrm{2}\mid\:{continue} \\ $$$${to}\:{decrease}…{so}\:\mid{x}+\mathrm{2}\mid\:{has}\:{no}\:{min}\:{value} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
ii)g(x)=−∣x+1∣+3 critical value of x=−1 at x=−1 g(x)=3 now when x>−1 and we increase x keeping condition x>−1 value of g(x) decreases so it has no min value... when x<−1 we continue decrease the value of x...then the value of x+1<0 so −∣x+1∣ become +ve...thus the value of g(x) increases ...thus g(x) has no max value
$$\left.{ii}\right){g}\left({x}\right)=−\mid{x}+\mathrm{1}\mid+\mathrm{3} \\ $$$${critical}\:{value}\:{of}\:{x}=−\mathrm{1} \\ $$$${at}\:{x}=−\mathrm{1}\:\:{g}\left({x}\right)=\mathrm{3} \\ $$$${now}\:{when}\:{x}>−\mathrm{1}\:{and}\:{we}\:{increase}\:{x}\:{keeping} \\ $$$${condition}\:{x}>−\mathrm{1}\:{value}\:{of}\:{g}\left({x}\right)\:{decreases} \\ $$$${so}\:{it}\:{has}\:{no}\:{min}\:{value}… \\ $$$${when}\:{x}<−\mathrm{1}\:\:{we}\:{continue}\:{decrease}\:{the} \\ $$$${value}\:{of}\:{x}…{then}\:{the}\:{value}\:{of}\:{x}+\mathrm{1}<\mathrm{0} \\ $$$${so}\:−\mid{x}+\mathrm{1}\mid\:{become}\:+{ve}…{thus}\:{the}\:{value} \\ $$$${of}\:{g}\left({x}\right)\:{increases}\:…{thus}\:{g}\left({x}\right)\:{has}\:{no}\:{max}\:{value} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
iv)for any value of x,min value of sin4x=−1 max value of sin4x=+1 so min value of f(x)=∣−1+3∣=2 max value f(x)=∣1+3∣=4 if the problem is f(x)=∣sin(4x+3)∣ then min value of sin(4x+3)=−1 thdn max value of sin(4x+3)=1 but value of f(x)=∣−1∣=1 f(x)=∣1∣=1 so f(x) has no min no max value... so
$$\left.{iv}\right){for}\:{any}\:{value}\:{of}\:{x},{min}\:{value}\:{of}\:{sin}\mathrm{4}{x}=−\mathrm{1} \\ $$$${max}\:{value}\:{of}\:{sin}\mathrm{4}{x}=+\mathrm{1} \\ $$$${so}\:{min}\:{value}\:{of}\:{f}\left({x}\right)=\mid−\mathrm{1}+\mathrm{3}\mid=\mathrm{2} \\ $$$${max}\:{value}\:{f}\left({x}\right)=\mid\mathrm{1}+\mathrm{3}\mid=\mathrm{4} \\ $$$${if}\:{the}\:{problem}\:{is}\:{f}\left({x}\right)=\mid{sin}\left(\mathrm{4}{x}+\mathrm{3}\right)\mid \\ $$$${then}\:{min}\:{value}\:{of}\:{sin}\left(\mathrm{4}{x}+\mathrm{3}\right)=−\mathrm{1} \\ $$$${thdn}\:{max}\:{value}\:{of}\:{sin}\left(\mathrm{4}{x}+\mathrm{3}\right)=\mathrm{1} \\ $$$${but}\:{value}\:{of}\:{f}\left({x}\right)=\mid−\mathrm{1}\mid=\mathrm{1} \\ $$$${f}\left({x}\right)=\mid\mathrm{1}\mid=\mathrm{1} \\ $$$${so}\:{f}\left({x}\right)\:{has}\:{no}\:{min}\:{no}\:{max}\:{value}… \\ $$$${so}\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
v)h(x)=x+1 as x→1 h(x)→2 x→−1 h(x)→0 so value of h(x) lies between 0 and 2 h(x) (0,2)...but the range of h(x) does not include lowes value 0 highest value 2 thus h(x) has no max or min value...
$$\left.{v}\right){h}\left({x}\right)={x}+\mathrm{1}\:\:{as}\:{x}\rightarrow\mathrm{1}\:\:{h}\left({x}\right)\rightarrow\mathrm{2} \\ $$$${x}\rightarrow−\mathrm{1}\:\:{h}\left({x}\right)\rightarrow\mathrm{0} \\ $$$${so}\:{value}\:{of}\:{h}\left({x}\right)\:\:{lies}\:{between}\:\mathrm{0}\:{and}\:\mathrm{2} \\ $$$${h}\left({x}\right)\:\:\left(\mathrm{0},\mathrm{2}\right)…{but}\:{the}\:{range}\:{of}\:{h}\left({x}\right)\:{does}\:{not} \\ $$$${include}\:{lowes}\:{value}\:\mathrm{0}\:{highest}\:{value}\:\mathrm{2} \\ $$$${thus}\:{h}\left({x}\right)\:{has}\:{no}\:{max}\:{or}\:{min}\:{value}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *