Question Number 39930 by Raj Singh last updated on 13/Jul/18

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
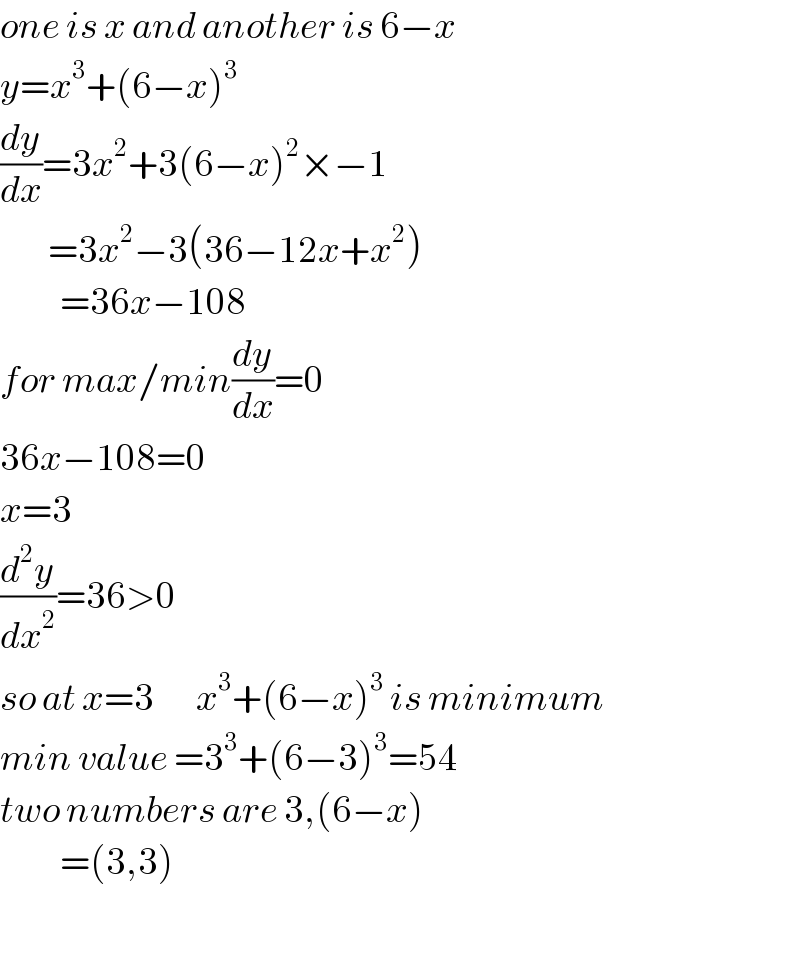
$${one}\:{is}\:{x}\:{and}\:{another}\:{is}\:\mathrm{6}−{x} \\ $$$${y}={x}^{\mathrm{3}} +\left(\mathrm{6}−{x}\right)^{\mathrm{3}} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}\left(\mathrm{6}−{x}\right)^{\mathrm{2}} ×−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{36}−\mathrm{12}{x}+{x}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{36}{x}−\mathrm{108} \\ $$$${for}\:{max}/{min}\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{36}{x}−\mathrm{108}=\mathrm{0} \\ $$$${x}=\mathrm{3} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{36}>\mathrm{0} \\ $$$${so}\:{at}\:{x}=\mathrm{3}\:\:\:\:\:\:\:{x}^{\mathrm{3}} +\left(\mathrm{6}−{x}\right)^{\mathrm{3}} \:{is}\:{minimum} \\ $$$${min}\:{value}\:=\mathrm{3}^{\mathrm{3}} +\left(\mathrm{6}−\mathrm{3}\right)^{\mathrm{3}} =\mathrm{54} \\ $$$${two}\:{numbers}\:{are}\:\mathrm{3},\left(\mathrm{6}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{3},\mathrm{3}\right) \\ $$$$ \\ $$
