Question Number 39970 by rahul 19 last updated on 14/Jul/18

Answered by MrW3 last updated on 14/Jul/18
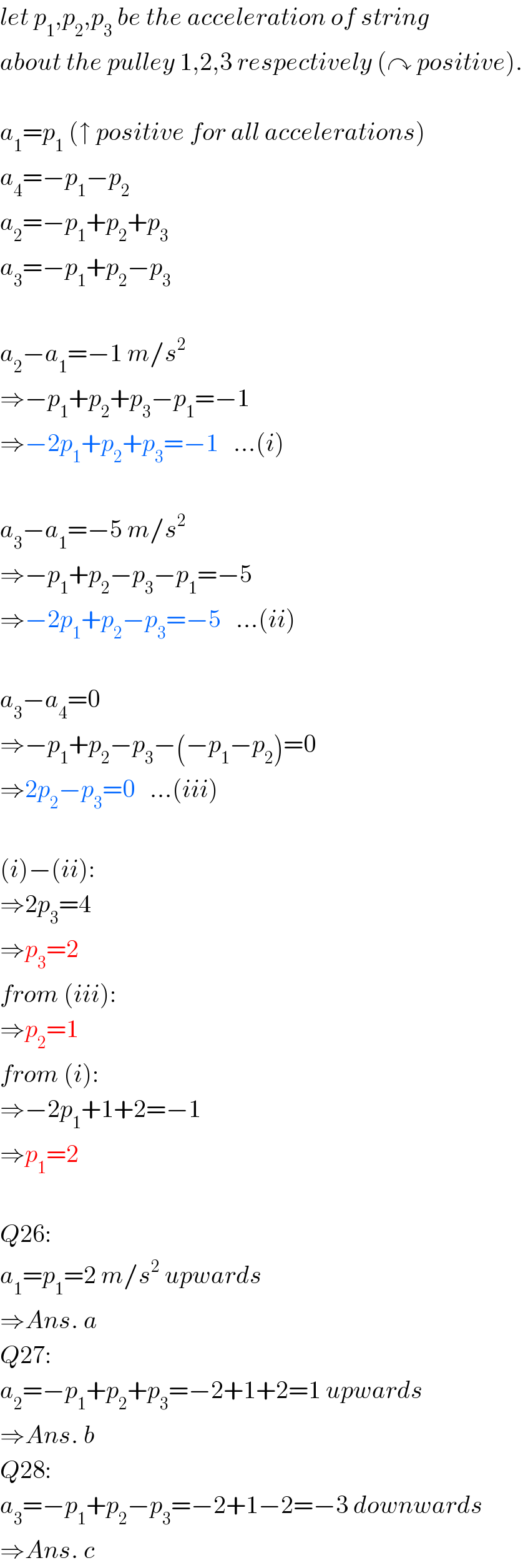
$${let}\:{p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,{p}_{\mathrm{3}} \:{be}\:{the}\:{acceleration}\:{of}\:{string} \\ $$$${about}\:{the}\:{pulley}\:\mathrm{1},\mathrm{2},\mathrm{3}\:{respectively}\:\left(\curvearrowright\:{positive}\right). \\ $$$$ \\ $$$${a}_{\mathrm{1}} ={p}_{\mathrm{1}} \:\left(\uparrow\:{positive}\:{for}\:{all}\:{accelerations}\right) \\ $$$${a}_{\mathrm{4}} =−{p}_{\mathrm{1}} −{p}_{\mathrm{2}} \\ $$$${a}_{\mathrm{2}} =−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} +{p}_{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} =−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} \\ $$$$ \\ $$$${a}_{\mathrm{2}} −{a}_{\mathrm{1}} =−\mathrm{1}\:{m}/{s}^{\mathrm{2}} \\ $$$$\Rightarrow−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} +{p}_{\mathrm{3}} −{p}_{\mathrm{1}} =−\mathrm{1} \\ $$$$\Rightarrow−\mathrm{2}{p}_{\mathrm{1}} +{p}_{\mathrm{2}} +{p}_{\mathrm{3}} =−\mathrm{1}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${a}_{\mathrm{3}} −{a}_{\mathrm{1}} =−\mathrm{5}\:{m}/{s}^{\mathrm{2}} \\ $$$$\Rightarrow−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} −{p}_{\mathrm{1}} =−\mathrm{5} \\ $$$$\Rightarrow−\mathrm{2}{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} =−\mathrm{5}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${a}_{\mathrm{3}} −{a}_{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} −\left(−{p}_{\mathrm{1}} −{p}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{p}_{\mathrm{2}} −{p}_{\mathrm{3}} =\mathrm{0}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\Rightarrow\mathrm{2}{p}_{\mathrm{3}} =\mathrm{4} \\ $$$$\Rightarrow{p}_{\mathrm{3}} =\mathrm{2} \\ $$$${from}\:\left({iii}\right): \\ $$$$\Rightarrow{p}_{\mathrm{2}} =\mathrm{1} \\ $$$${from}\:\left({i}\right): \\ $$$$\Rightarrow−\mathrm{2}{p}_{\mathrm{1}} +\mathrm{1}+\mathrm{2}=−\mathrm{1} \\ $$$$\Rightarrow{p}_{\mathrm{1}} =\mathrm{2} \\ $$$$ \\ $$$${Q}\mathrm{26}: \\ $$$${a}_{\mathrm{1}} ={p}_{\mathrm{1}} =\mathrm{2}\:{m}/{s}^{\mathrm{2}} \:{upwards} \\ $$$$\Rightarrow{Ans}.\:{a} \\ $$$${Q}\mathrm{27}: \\ $$$${a}_{\mathrm{2}} =−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} +{p}_{\mathrm{3}} =−\mathrm{2}+\mathrm{1}+\mathrm{2}=\mathrm{1}\:{upwards} \\ $$$$\Rightarrow{Ans}.\:{b} \\ $$$${Q}\mathrm{28}: \\ $$$${a}_{\mathrm{3}} =−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} =−\mathrm{2}+\mathrm{1}−\mathrm{2}=−\mathrm{3}\:{downwards} \\ $$$$\Rightarrow{Ans}.\:{c} \\ $$
Commented by rahul 19 last updated on 15/Jul/18

$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{to}\:\mathrm{write}\:\mathrm{the}\:\mathrm{initial}\:\mathrm{3}\:\mathrm{eq}.\mathrm{s} \\ $$$$\mathrm{a}_{\mathrm{4}} =\:−\mathrm{p}_{\mathrm{1}} −\mathrm{p}_{\mathrm{2}} \\ $$$$\mathrm{a}_{\mathrm{2}} =−\mathrm{p}_{\mathrm{1}} +\mathrm{p}_{\mathrm{2}} +\mathrm{p}_{\mathrm{3}} \\ $$$$\mathrm{a}_{\mathrm{3}} =−\mathrm{p}_{\mathrm{1}} +\mathrm{p}_{\mathrm{2}} −\mathrm{p}_{\mathrm{3}} \:? \\ $$$$\mathrm{Need}\:\mathrm{more}\:\mathrm{explaination}! \\ $$
Commented by MrW3 last updated on 15/Jul/18

Commented by MrW3 last updated on 15/Jul/18

$${Each}\:{string}\:{rolls}\:{about}\:{a}\:{pulley}.\:{Let}'{s} \\ $$$${say}\:{the}\:{acceleration}\:{of}\:{the}\:{strings}\:{are} \\ $$$${p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,{p}_{\mathrm{3}} \:{respectively}. \\ $$$${Pulley}\:{I}\:{is}\:{fixed},\:{therefore}\:{the} \\ $$$${acceleration}\:{of}\:{block}\:\mathrm{1}\:{is} \\ $$$${a}_{\mathrm{1}} ={p}_{\mathrm{1}} \:\left({upwards},\:{hence}\:+{ve}\right) \\ $$$${and}\:{the}\:{acceleration}\:{of}\:{pulley}\:{II}\:{is} \\ $$$${a}_{{II}} =−{p}_{\mathrm{1}} \:\left({downwards},\:{hence}\:−{ve}\right). \\ $$$${Block}\:\mathrm{4}\:{moves}\:{relatively}\:{to}\:{pulley}\:{II} \\ $$$${with}\:{p}_{\mathrm{2}} ,\:{therefore} \\ $$$${a}_{\mathrm{4}} ={a}_{{II}} −{p}_{\mathrm{2}} =−{p}_{\mathrm{1}} −{p}_{\mathrm{2}} \\ $$$${Similarly} \\ $$$${a}_{{III}} ={a}_{{II}} +{p}_{\mathrm{2}} =−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} \\ $$$${Block}\:\mathrm{2}\:{and}\:\mathrm{3}\:{move}\:{relatively}\:{to}\: \\ $$$${pulley}\:{III}\:{with}\:{p}_{\mathrm{3}} ,\:{hence} \\ $$$${a}_{\mathrm{3}} ={a}_{{III}} −{p}_{\mathrm{3}} \:=−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} −{p}_{\mathrm{3}} \:{and} \\ $$$${a}_{\mathrm{2}} ={a}_{{III}} +{p}_{\mathrm{3}} \:=−{p}_{\mathrm{1}} +{p}_{\mathrm{2}} +{p}_{\mathrm{3}} \\ $$
Commented by MrW3 last updated on 15/Jul/18
$${I}\:{hope}\:{it}'{s}\:{clear}\:{now}. \\ $$
Commented by rahul 19 last updated on 15/Jul/18
Thank you so much sir ! ��������
