Menu Close

Question-39985

Tinku Tara 0 Comments
Pin




Question Number 39985 by ajfour last updated on 14/Jul/18
Answered by ajfour last updated on 15/Jul/18
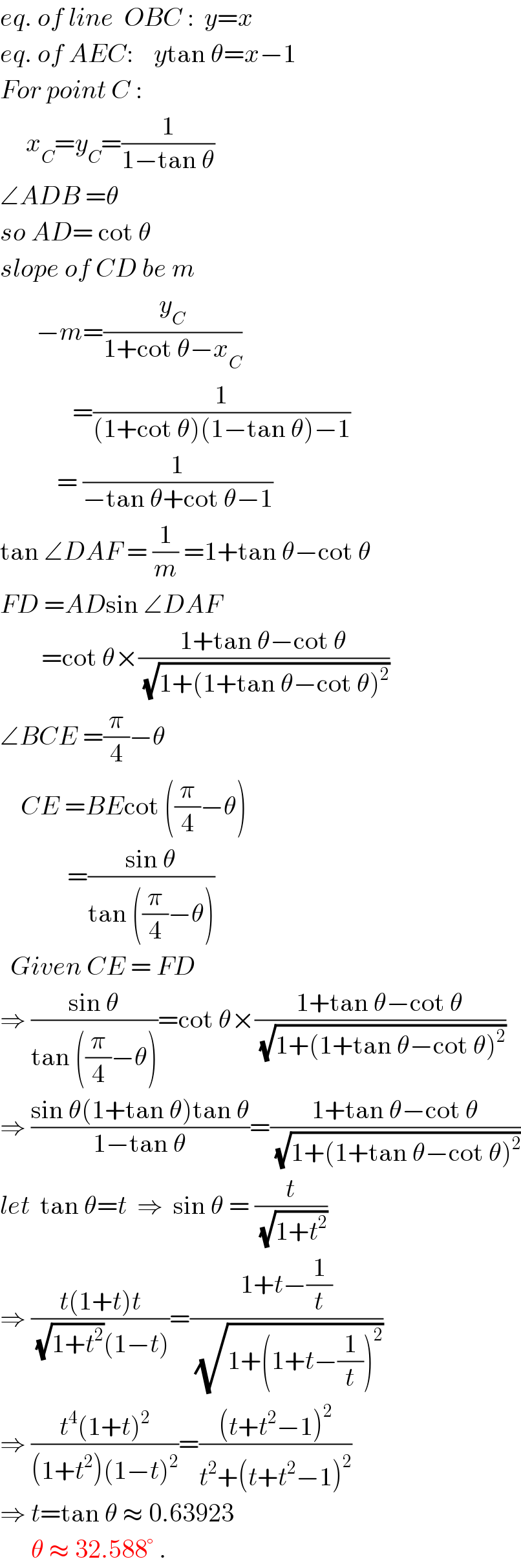
eq. of line OBC : y=x eq. of AEC: ytan θ=x−1 For point C : x_C =y_C =(1/(1−tan θ)) ∠ADB =θ so AD= cot θ slope of CD be m −m=(y_C /(1+cot θ−x_C )) =(1/((1+cot θ)(1−tan θ)−1)) = (1/(−tan θ+cot θ−1)) tan ∠DAF = (1/m) =1+tan θ−cot θ FD =ADsin ∠DAF =cot θ×((1+tan θ−cot θ)/( (√(1+(1+tan θ−cot θ)^2 )))) ∠BCE =(π/4)−θ CE =BEcot ((π/4)−θ) =((sin θ)/(tan ((π/4)−θ))) Given CE = FD ⇒ ((sin θ)/(tan ((π/4)−θ)))=cot θ×((1+tan θ−cot θ)/( (√(1+(1+tan θ−cot θ)^2 )))) ⇒ ((sin θ(1+tan θ)tan θ)/(1−tan θ))=((1+tan θ−cot θ)/( (√(1+(1+tan θ−cot θ)^2 )))) let tan θ=t ⇒ sin θ = (t/( (√(1+t^2 )))) ⇒ ((t(1+t)t)/( (√(1+t^2 ))(1−t)))=((1+t−(1/t))/( (√(1+(1+t−(1/t))^2 )))) ⇒ ((t^4 (1+t)^2 )/((1+t^2 )(1−t)^2 ))=(((t+t^2 −1)^2 )/(t^2 +(t+t^2 −1)^2 )) ⇒ t=tan θ ≈ 0.63923 θ ≈ 32.588° .
$${eq}.\:{of}\:{line}\:\:{OBC}\::\:\:{y}={x} \\ $$$${eq}.\:{of}\:{AEC}:\:\:\:\:{y}\mathrm{tan}\:\theta={x}−\mathrm{1} \\ $$$${For}\:{point}\:{C}\:: \\ $$$$\:\:\:\:\:{x}_{{C}} ={y}_{{C}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\theta}\:\: \\ $$$$\angle{ADB}\:=\theta \\ $$$${so}\:{AD}=\:\mathrm{cot}\:\theta \\ $$$${slope}\:{of}\:{CD}\:{be}\:{m} \\ $$$$\:\:\:\:\:\:\:−{m}=\frac{{y}_{{C}} }{\mathrm{1}+\mathrm{cot}\:\theta−{x}_{{C}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{cot}\:\theta\right)\left(\mathrm{1}−\mathrm{tan}\:\theta\right)−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{−\mathrm{tan}\:\theta+\mathrm{cot}\:\theta−\mathrm{1}} \\ $$$$\mathrm{tan}\:\angle{DAF}\:=\:\frac{\mathrm{1}}{{m}}\:=\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta \\ $$$${FD}\:={AD}\mathrm{sin}\:\angle{DAF} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{cot}\:\theta×\frac{\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta\right)^{\mathrm{2}} }} \\ $$$$\angle{BCE}\:=\frac{\pi}{\mathrm{4}}−\theta \\ $$$$\:\:\:\:{CE}\:={BE}\mathrm{cot}\:\left(\frac{\pi}{\mathrm{4}}−\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\theta\right)} \\ $$$$\:\:{Given}\:{CE}\:=\:{FD} \\ $$$$\Rightarrow\:\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\theta\right)}=\mathrm{cot}\:\theta×\frac{\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\frac{\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{tan}\:\theta\right)\mathrm{tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:\theta}=\frac{\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+\mathrm{tan}\:\theta−\mathrm{cot}\:\theta\right)^{\mathrm{2}} }} \\ $$$${let}\:\:\mathrm{tan}\:\theta={t}\:\:\Rightarrow\:\:\mathrm{sin}\:\theta\:=\:\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\frac{{t}\left(\mathrm{1}+{t}\right){t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\left(\mathrm{1}−{t}\right)}=\frac{\mathrm{1}+{t}−\frac{\mathrm{1}}{{t}}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}+{t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\frac{{t}^{\mathrm{4}} \left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }=\frac{\left({t}+{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +\left({t}+{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:{t}=\mathrm{tan}\:\theta\:\approx\:\mathrm{0}.\mathrm{63923} \\ $$$$\:\:\:\:\:\:\theta\:\approx\:\mathrm{32}.\mathrm{588}°\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *