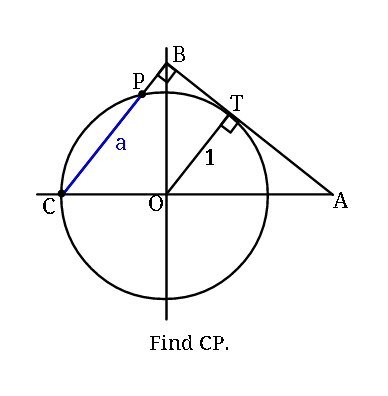
Question Number 39993 by ajfour last updated on 14/Jul/18
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Jul/18

$${let}\:\angle{AOT}=\theta \\ $$$${OT}\parallel\:{toBC}\:{so}\:\frac{{AO}}{{AC}}=\frac{{AT}}{{AB}}=\frac{{OT}}{{BC}} \\ $$$${point}\:{T}\left({cos}\theta,{sin}\theta\right)\:\:{andpoint}\:{C}\left(−\mathrm{1},\mathrm{0}\right) \\ $$$${eqn}\:\:\:{of}\:{OT}\:{is}\:{y}={xtan}\theta \\ $$$${eqn}\:{ofCB}\:{is}\:{y}=\left({x}+\mathrm{1}\right){tan}\theta \\ $$$${eqn}\:{of}\:{circle}\:{is}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${solve}\:{y}=\left({x}+\mathrm{1}\right){tan}\theta\:{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{x}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta+\mathrm{2}{xtan}^{\mathrm{2}} \theta+{tan}^{\mathrm{2}} \theta−\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({sec}^{\mathrm{2}} \theta\right)+{x}\left(\mathrm{2}{tan}^{\mathrm{2}} \theta\right)+{tan}^{\mathrm{2}} \theta−\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{xsin}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta−{cos}^{\mathrm{2}} \theta=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{x}\left(\mathrm{1}−{cos}\mathrm{2}\theta\right)−\left({cos}\mathrm{2}\theta\right)=\mathrm{0} \\ $$$${x}=\frac{−\left(\mathrm{1}−{cos}\mathrm{2}\theta\right)\pm\sqrt{\mathrm{1}−\mathrm{2}{cos}\mathrm{2}\theta+{cos}^{\mathrm{2}} \mathrm{2}\theta+\mathrm{4}{cos}\mathrm{2}\theta}}{\mathrm{2}} \\ $$$${x}=\frac{−\left(\mathrm{1}−{cos}\mathrm{2}\theta\right)\pm\left(\mathrm{1}+{cos}\mathrm{2}\theta\right)}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{1}+{cos}\mathrm{2}\theta+\mathrm{1}+{cos}\mathrm{2}\theta}{\mathrm{2}},\frac{−\mathrm{1}+{cos}\mathrm{2}\theta−\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}} \\ $$$${x}={cos}\mathrm{2}\theta,−\mathrm{1}\: \\ $$$${when}\:{x}={cos}\mathrm{2}\theta\:\:{y}={sin}\mathrm{2}\theta \\ $$$${when}\:{x}=−\mathrm{1}\:\:{so}\:{y}=\mathrm{0} \\ $$$${so}\:{point}\:{C}\left(−\mathrm{1},\mathrm{0}\right)\:{point}\:{P}\left({cos}\mathrm{2}\theta,{sin}\mathrm{2}\theta\right) \\ $$$${CP}=\sqrt{\left({cos}\mathrm{2}\theta\:+\mathrm{1}\right)^{\mathrm{2}} +\left({sin}\mathrm{2}\theta\right)^{\mathrm{2}} } \\ $$$$\:\:=\sqrt{{co}_{} {s}^{\mathrm{2}} \mathrm{2}\theta+\mathrm{2}{cos}\mathrm{2}\theta+\mathrm{1}+{sin}^{\mathrm{2}} \mathrm{2}\theta} \\ $$$$=\sqrt{\mathrm{2}\left(\mathrm{1}+{cos}\mathrm{2}\theta\right)} \\ $$$$=\sqrt{\mathrm{4}{cos}^{\mathrm{2}} \theta}=\mathrm{2}{cos}\theta\:\:{where}\:\theta=\angle{AOT} \\ $$$${wait}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 15/Jul/18
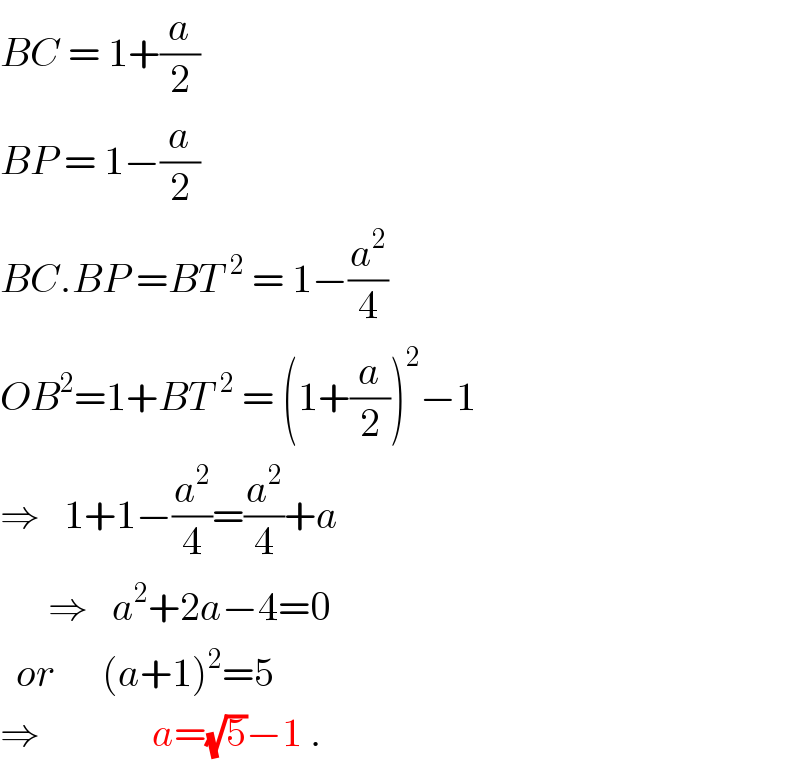
$${BC}\:=\:\mathrm{1}+\frac{{a}}{\mathrm{2}} \\ $$$${BP}\:=\:\mathrm{1}−\frac{{a}}{\mathrm{2}} \\ $$$${BC}.{BP}\:={BT}^{\:\:\mathrm{2}} \:=\:\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${OB}^{\mathrm{2}} =\mathrm{1}+{BT}^{\:\:\mathrm{2}} \:=\:\left(\mathrm{1}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:\:\:\mathrm{1}+\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{a} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\:{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{4}=\mathrm{0} \\ $$$$\:\:{or}\:\:\:\:\:\:\left({a}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{5} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\sqrt{\mathrm{5}}−\mathrm{1}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jul/18
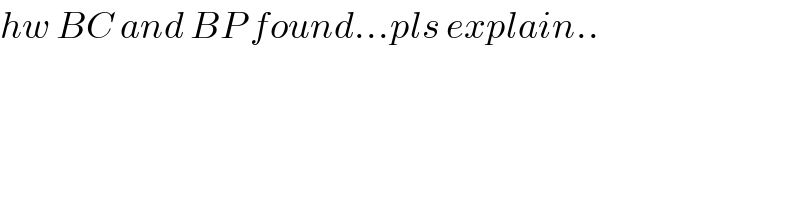
$${hw}\:{BC}\:{and}\:{BP}\:{found}…{pls}\:{explain}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jul/18

$${yes}\:{i}\:{got}\:{it}..{perpedicuar}\:{from}\:{centre}\:{bisect}\:{the} \\ $$$${chord}…{and}\:{perpendicular}\:{from}\:{centre} \\ $$$${make}\:{a}\:{rectangle}…{opposite}\:{side}\:{are}\:{same}\:{equals}\: \\ $$$${to}\:\mathrm{1} \\ $$
