Menu Close

Question-39995

Tinku Tara 0 Comments
Pin




Question Number 39995 by behi83417@gmail.com last updated on 14/Jul/18
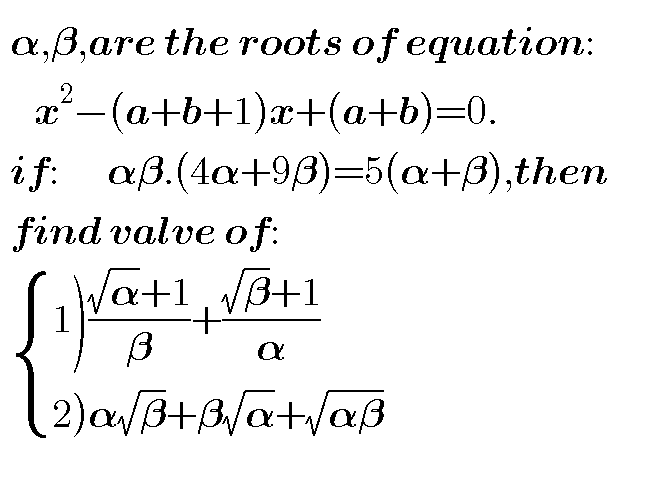
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jul/18
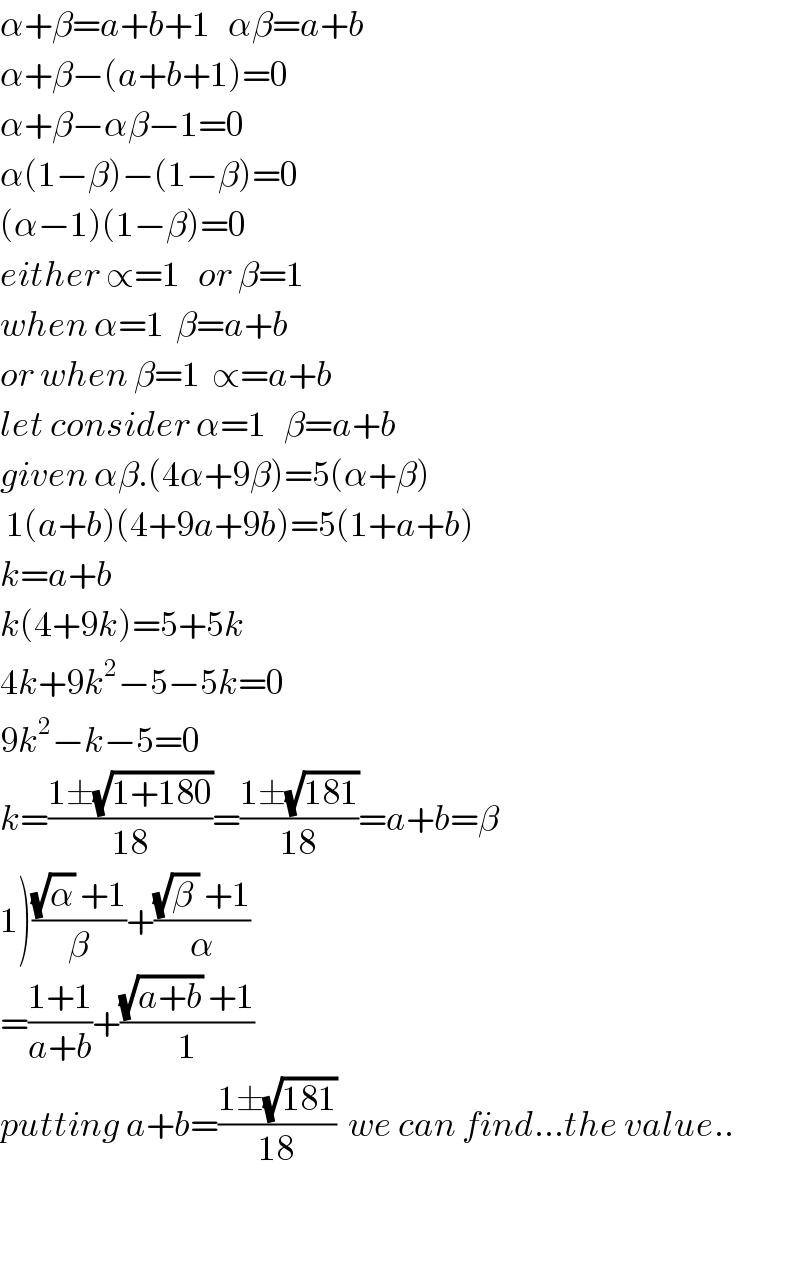
α+β=a+b+1 αβ=a+b α+β−(a+b+1)=0 α+β−αβ−1=0 α(1−β)−(1−β)=0 (α−1)(1−β)=0 either ∝=1 or β=1 when α=1 β=a+b or when β=1 ∝=a+b let consider α=1 β=a+b given αβ.(4α+9β)=5(α+β) 1(a+b)(4+9a+9b)=5(1+a+b) k=a+b k(4+9k)=5+5k 4k+9k^2 −5−5k=0 9k^2 −k−5=0 k=((1±(√(1+180)))/(18))=((1±(√(181)))/(18))=a+b=β 1)(((√α) +1)/β)+(((√(β )) +1)/α) =((1+1)/(a+b))+(((√(a+b)) +1)/1) putting a+b=((1±(√(181)))/(18)) we can find...the value..
$$\alpha+\beta={a}+{b}+\mathrm{1}\:\:\:\alpha\beta={a}+{b} \\ $$$$\alpha+\beta−\left({a}+{b}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\alpha+\beta−\alpha\beta−\mathrm{1}=\mathrm{0} \\ $$$$\alpha\left(\mathrm{1}−\beta\right)−\left(\mathrm{1}−\beta\right)=\mathrm{0} \\ $$$$\left(\alpha−\mathrm{1}\right)\left(\mathrm{1}−\beta\right)=\mathrm{0} \\ $$$${either}\:\propto=\mathrm{1}\:\:\:{or}\:\beta=\mathrm{1} \\ $$$${when}\:\alpha=\mathrm{1}\:\:\beta={a}+{b} \\ $$$${or}\:{when}\:\beta=\mathrm{1}\:\:\propto={a}+{b} \\ $$$${let}\:{consider}\:\alpha=\mathrm{1}\:\:\:\beta={a}+{b} \\ $$$${given}\:\alpha\beta.\left(\mathrm{4}\alpha+\mathrm{9}\beta\right)=\mathrm{5}\left(\alpha+\beta\right) \\ $$$$\:\mathrm{1}\left({a}+{b}\right)\left(\mathrm{4}+\mathrm{9}{a}+\mathrm{9}{b}\right)=\mathrm{5}\left(\mathrm{1}+{a}+{b}\right) \\ $$$${k}={a}+{b} \\ $$$${k}\left(\mathrm{4}+\mathrm{9}{k}\right)=\mathrm{5}+\mathrm{5}{k} \\ $$$$\mathrm{4}{k}+\mathrm{9}{k}^{\mathrm{2}} −\mathrm{5}−\mathrm{5}{k}=\mathrm{0} \\ $$$$\mathrm{9}{k}^{\mathrm{2}} −{k}−\mathrm{5}=\mathrm{0} \\ $$$${k}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{180}}}{\mathrm{18}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{181}}}{\mathrm{18}}={a}+{b}=\beta \\ $$$$\left.\mathrm{1}\right)\frac{\sqrt{\alpha}\:+\mathrm{1}}{\beta}+\frac{\sqrt{\beta\:}\:+\mathrm{1}}{\alpha} \\ $$$$=\frac{\mathrm{1}+\mathrm{1}}{{a}+{b}}+\frac{\sqrt{{a}+{b}}\:+\mathrm{1}}{\mathrm{1}} \\ $$$${putting}\:{a}+{b}=\frac{\mathrm{1}\pm\sqrt{\mathrm{181}}}{\mathrm{18}}\:\:{we}\:{can}\:{find}…{the}\:{value}.. \\ $$$$ \\ $$
Answered by MJS last updated on 15/Jul/18
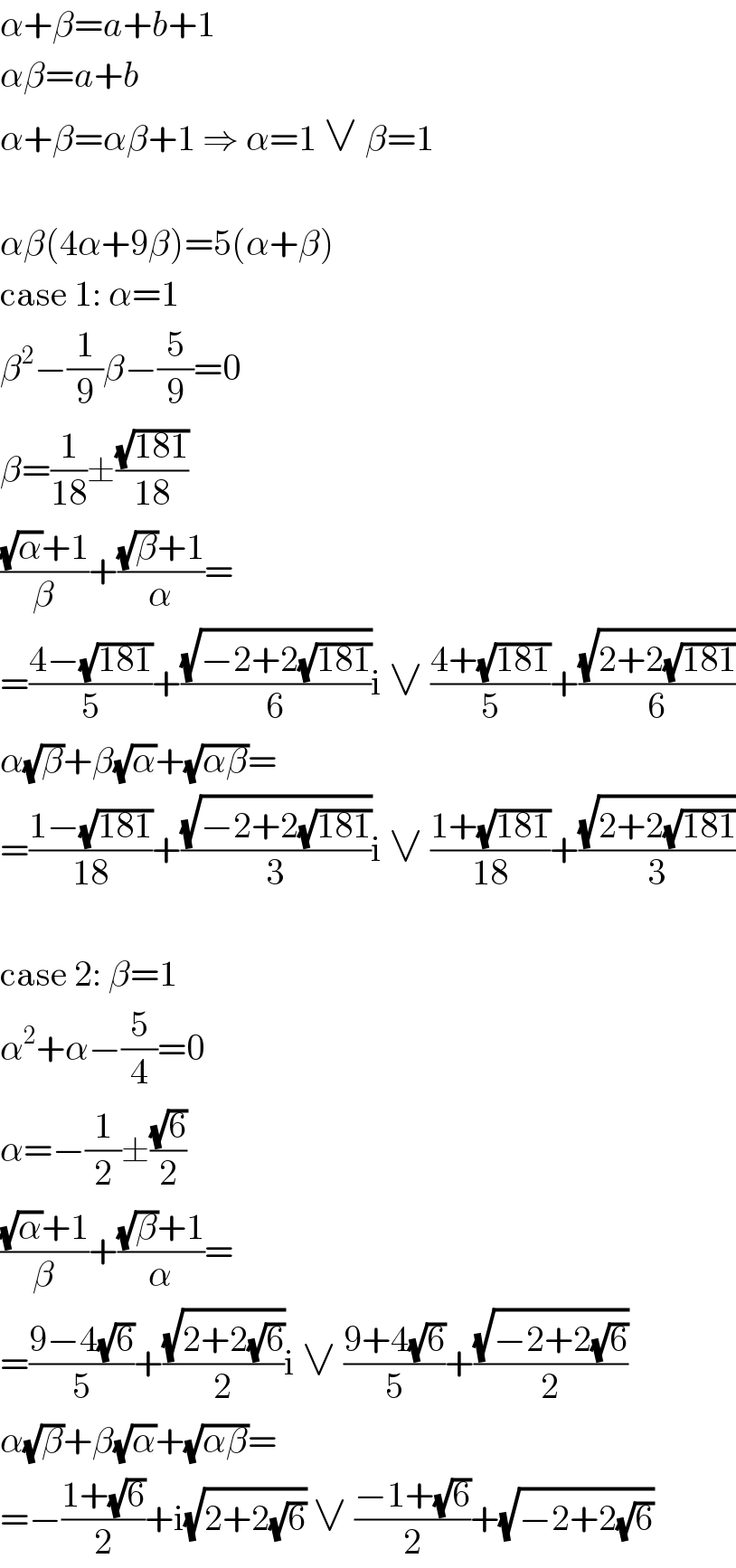
α+β=a+b+1 αβ=a+b α+β=αβ+1 ⇒ α=1 ∨ β=1 αβ(4α+9β)=5(α+β) case 1: α=1 β^2 −(1/9)β−(5/9)=0 β=(1/(18))±((√(181))/(18)) (((√α)+1)/β)+(((√β)+1)/α)= =((4−(√(181)))/5)+((√(−2+2(√(181))))/6)i ∨ ((4+(√(181)))/5)+((√(2+2(√(181))))/6) α(√β)+β(√α)+(√(αβ))= =((1−(√(181)))/(18))+((√(−2+2(√(181))))/3)i ∨ ((1+(√(181)))/(18))+((√(2+2(√(181))))/3) case 2: β=1 α^2 +α−(5/4)=0 α=−(1/2)±((√6)/2) (((√α)+1)/β)+(((√β)+1)/α)= =((9−4(√6))/5)+((√(2+2(√6)))/2)i ∨ ((9+4(√6))/5)+((√(−2+2(√6)))/2) α(√β)+β(√α)+(√(αβ))= =−((1+(√6))/2)+i(√(2+2(√6))) ∨ ((−1+(√6))/2)+(√(−2+2(√6)))
$$\alpha+\beta={a}+{b}+\mathrm{1} \\ $$$$\alpha\beta={a}+{b} \\ $$$$\alpha+\beta=\alpha\beta+\mathrm{1}\:\Rightarrow\:\alpha=\mathrm{1}\:\vee\:\beta=\mathrm{1} \\ $$$$ \\ $$$$\alpha\beta\left(\mathrm{4}\alpha+\mathrm{9}\beta\right)=\mathrm{5}\left(\alpha+\beta\right) \\ $$$$\mathrm{case}\:\mathrm{1}:\:\alpha=\mathrm{1} \\ $$$$\beta^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{9}}\beta−\frac{\mathrm{5}}{\mathrm{9}}=\mathrm{0} \\ $$$$\beta=\frac{\mathrm{1}}{\mathrm{18}}\pm\frac{\sqrt{\mathrm{181}}}{\mathrm{18}} \\ $$$$\frac{\sqrt{\alpha}+\mathrm{1}}{\beta}+\frac{\sqrt{\beta}+\mathrm{1}}{\alpha}= \\ $$$$=\frac{\mathrm{4}−\sqrt{\mathrm{181}}}{\mathrm{5}}+\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{181}}}}{\mathrm{6}}\mathrm{i}\:\vee\:\frac{\mathrm{4}+\sqrt{\mathrm{181}}}{\mathrm{5}}+\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{181}}}}{\mathrm{6}} \\ $$$$\alpha\sqrt{\beta}+\beta\sqrt{\alpha}+\sqrt{\alpha\beta}= \\ $$$$=\frac{\mathrm{1}−\sqrt{\mathrm{181}}}{\mathrm{18}}+\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{181}}}}{\mathrm{3}}\mathrm{i}\:\vee\:\frac{\mathrm{1}+\sqrt{\mathrm{181}}}{\mathrm{18}}+\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{181}}}}{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{2}:\:\beta=\mathrm{1} \\ $$$$\alpha^{\mathrm{2}} +\alpha−\frac{\mathrm{5}}{\mathrm{4}}=\mathrm{0} \\ $$$$\alpha=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$$\frac{\sqrt{\alpha}+\mathrm{1}}{\beta}+\frac{\sqrt{\beta}+\mathrm{1}}{\alpha}= \\ $$$$=\frac{\mathrm{9}−\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{5}}+\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}}}{\mathrm{2}}\mathrm{i}\:\vee\:\frac{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{5}}+\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}}}{\mathrm{2}} \\ $$$$\alpha\sqrt{\beta}+\beta\sqrt{\alpha}+\sqrt{\alpha\beta}= \\ $$$$=−\frac{\mathrm{1}+\sqrt{\mathrm{6}}}{\mathrm{2}}+\mathrm{i}\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}}\:\vee\:\frac{−\mathrm{1}+\sqrt{\mathrm{6}}}{\mathrm{2}}+\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jul/18
thank u sir...
$${thank}\:{u}\:{sir}… \\ $$
Commented by behi83417@gmail.com last updated on 15/Jul/18
thank you sir MJS and sir tanmay.
$${thank}\:{you}\:{sir}\:{MJS}\:{and}\:{sir}\:{tanmay}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *