Menu Close

Question-40063

Tinku Tara 0 Comments
Pin




Question Number 40063 by ajfour last updated on 15/Jul/18
Answered by ajfour last updated on 16/Jul/18
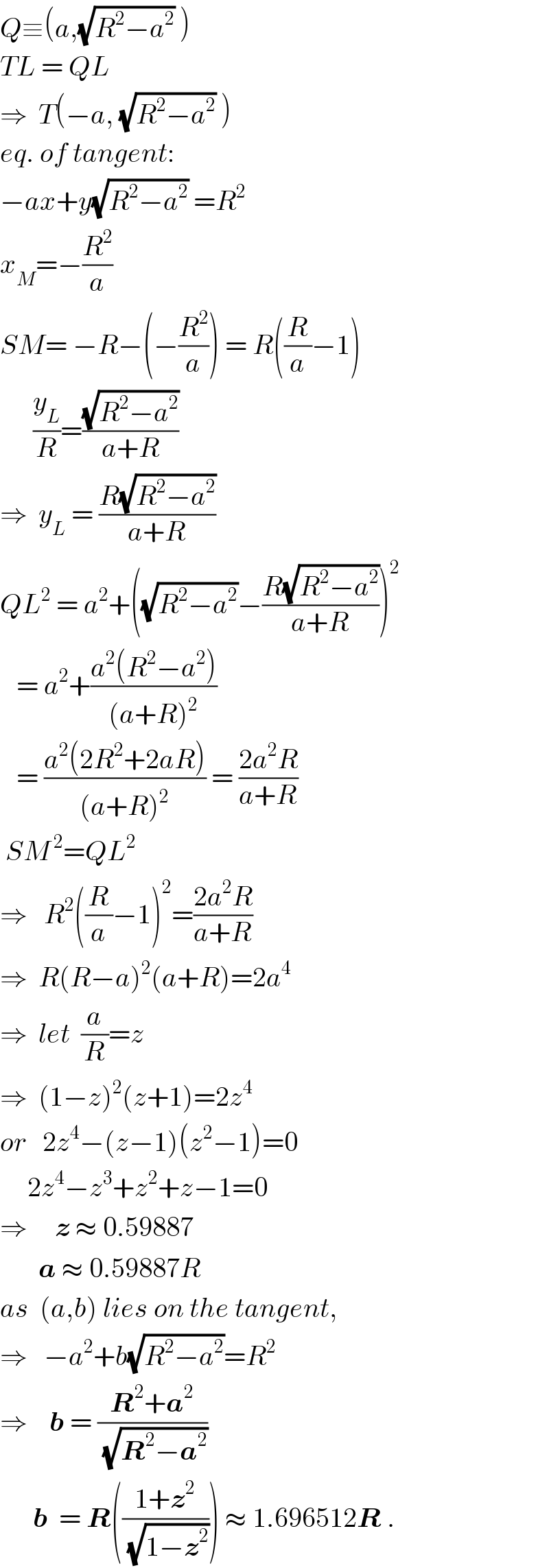
Q≡(a,(√(R^2 −a^2 )) ) TL = QL ⇒ T(−a, (√(R^2 −a^2 )) ) eq. of tangent: −ax+y(√(R^2 −a^2 )) =R^2 x_M =−(R^2 /a) SM= −R−(−(R^2 /a)) = R((R/a)−1) (y_L /R)=((√(R^2 −a^2 ))/(a+R)) ⇒ y_L = ((R(√(R^2 −a^2 )))/(a+R)) QL^2 = a^2 +((√(R^2 −a^2 ))−((R(√(R^2 −a^2 )))/(a+R)))^2 = a^2 +((a^2 (R^2 −a^2 ))/((a+R)^2 )) = ((a^2 (2R^2 +2aR))/((a+R)^2 )) = ((2a^2 R)/(a+R)) SM^( 2) =QL^2 ⇒ R^2 ((R/a)−1)^2 =((2a^2 R)/(a+R)) ⇒ R(R−a)^2 (a+R)=2a^4 ⇒ let (a/R)=z ⇒ (1−z)^2 (z+1)=2z^4 or 2z^4 −(z−1)(z^2 −1)=0 2z^4 −z^3 +z^2 +z−1=0 ⇒ z ≈ 0.59887 a ≈ 0.59887R as (a,b) lies on the tangent, ⇒ −a^2 +b(√(R^2 −a^2 ))=R^2 ⇒ b = ((R^2 +a^2 )/( (√(R^2 −a^2 )))) b = R(((1+z^2 )/( (√(1−z^2 ))))) ≈ 1.696512R .
$${Q}\equiv\left({a},\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:\right) \\ $$$${TL}\:=\:{QL} \\ $$$$\Rightarrow\:\:{T}\left(−{a},\:\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:\right) \\ $$$${eq}.\:{of}\:{tangent}: \\ $$$$−{ax}+{y}\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:={R}^{\mathrm{2}} \\ $$$${x}_{{M}} =−\frac{{R}^{\mathrm{2}} }{{a}} \\ $$$${SM}=\:−{R}−\left(−\frac{{R}^{\mathrm{2}} }{{a}}\right)\:=\:{R}\left(\frac{{R}}{{a}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\frac{{y}_{{L}} }{{R}}=\frac{\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}+{R}} \\ $$$$\Rightarrow\:\:{y}_{{L}} \:=\:\frac{{R}\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}+{R}} \\ $$$${QL}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} +\left(\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\frac{{R}\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}+{R}}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\:{a}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\left({a}+{R}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{{a}^{\mathrm{2}} \left(\mathrm{2}{R}^{\mathrm{2}} +\mathrm{2}{aR}\right)}{\left({a}+{R}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{2}{a}^{\mathrm{2}} {R}}{{a}+{R}} \\ $$$$\:{SM}^{\:\mathrm{2}} ={QL}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{R}^{\mathrm{2}} \left(\frac{{R}}{{a}}−\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{2}{a}^{\mathrm{2}} {R}}{{a}+{R}} \\ $$$$\Rightarrow\:\:{R}\left({R}−{a}\right)^{\mathrm{2}} \left({a}+{R}\right)=\mathrm{2}{a}^{\mathrm{4}} \\ $$$$\Rightarrow\:\:{let}\:\:\frac{{a}}{{R}}={z} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{z}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)=\mathrm{2}{z}^{\mathrm{4}} \\ $$$${or}\:\:\:\mathrm{2}{z}^{\mathrm{4}} −\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{2}{z}^{\mathrm{4}} −{z}^{\mathrm{3}} +{z}^{\mathrm{2}} +{z}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\boldsymbol{{z}}\:\approx\:\mathrm{0}.\mathrm{59887} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{a}}\:\approx\:\mathrm{0}.\mathrm{59887}{R} \\ $$$${as}\:\:\left({a},{b}\right)\:{lies}\:{on}\:{the}\:{tangent}, \\ $$$$\Rightarrow\:\:\:−{a}^{\mathrm{2}} +{b}\sqrt{{R}^{\mathrm{2}} −{a}^{\mathrm{2}} }={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\boldsymbol{{b}}\:=\:\frac{\boldsymbol{{R}}^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} }{\:\sqrt{\boldsymbol{{R}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\boldsymbol{{b}}\:\:=\:\boldsymbol{{R}}\left(\frac{\mathrm{1}+\boldsymbol{{z}}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\boldsymbol{{z}}^{\mathrm{2}} }}\right)\:\approx\:\mathrm{1}.\mathrm{696512}\boldsymbol{{R}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *