Menu Close

Question-40170

Tinku Tara 0 Comments
Pin




Question Number 40170 by ajfour last updated on 16/Jul/18
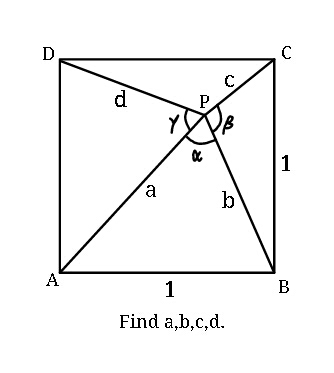
Commented by ajfour last updated on 16/Jul/18
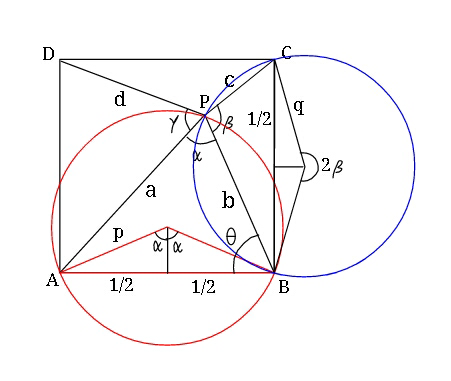
Commented by ajfour last updated on 16/Jul/18
p=(1/(2sin α)) q=(1/(2sin β)) lets take B as origin and x-axis leftwards, y-axis upwards; eq. of red circle: (y−(1/(2tan α)))^2 +(x−(1/2))^2 =p^2 similarly eq. of blue circle: (y−(1/2))^2 +(x−(1/(2tan β)))^2 =q^2 eq. of common chord: ((1/2)−(1/(2tan α)))(2y−(1/2)−(1/(2tan α))) −((1/2)−(1/(2tan β)))(2x−(1/2)−(1/(2tan β))) =p^2 −q^2 slope of chord is tan θ = (((1/2)−(1/(2tan β)))/((1/2)−(1/(2tan α)))) ⇒ tan θ = ((tan α)/(tan β))(((tan β−1)/(tan α−1))) Now (a/(sin θ)) =(1/(sin α)) ⇒ a = ((sin 𝛉)/(sin 𝛂)) a =((cos α(tan β−1))/( (√(tan^2 α(tan β−1)^2 +tan^2 β(tan α−1)^2 )))) (c/(cos θ))=(1/(sin β)) c = ((cos 𝛃(tan α−1))/( (√(tan^2 α(tan β−1)^2 +tan^2 β(tan α−1)^2 )))) ....
$${p}=\frac{\mathrm{1}}{\mathrm{2sin}\:\alpha}\:\:\:\:\:\:{q}=\frac{\mathrm{1}}{\mathrm{2sin}\:\beta} \\ $$$${lets}\:{take}\:{B}\:{as}\:{origin}\:{and} \\ $$$${x}-{axis}\:{leftwards},\:{y}-{axis}\:{upwards}; \\ $$$${eq}.\:{of}\:{red}\:{circle}: \\ $$$$\left({y}−\frac{\mathrm{1}}{\mathrm{2tan}\:\alpha}\right)^{\mathrm{2}} +\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${similarly}\:{eq}.\:{of}\:{blue}\:{circle}: \\ $$$$\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({x}−\frac{\mathrm{1}}{\mathrm{2tan}\:\beta}\right)^{\mathrm{2}} ={q}^{\mathrm{2}} \\ $$$${eq}.\:{of}\:{common}\:{chord}: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\alpha}\right)\left(\mathrm{2}{y}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\alpha}\right) \\ $$$$\:\:\:\:−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\beta}\right)\left(\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\beta}\right) \\ $$$$\:\:\:\:={p}^{\mathrm{2}} −{q}^{\mathrm{2}} \\ $$$${slope}\:{of}\:{chord}\:{is} \\ $$$$\:\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\beta}}{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2tan}\:\alpha}} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta\:=\:\frac{\mathrm{tan}\:\alpha}{\mathrm{tan}\:\beta}\left(\frac{\mathrm{tan}\:\beta−\mathrm{1}}{\mathrm{tan}\:\alpha−\mathrm{1}}\right) \\ $$$${Now}\:\:\:\frac{{a}}{\mathrm{sin}\:\theta}\:=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$$$\:\:\Rightarrow\:\:\:\boldsymbol{{a}}\:=\:\frac{\mathrm{sin}\:\boldsymbol{\theta}}{\mathrm{sin}\:\boldsymbol{\alpha}} \\ $$$$\:\boldsymbol{{a}}\:=\frac{\mathrm{cos}\:\alpha\left(\mathrm{tan}\:\beta−\mathrm{1}\right)}{\:\sqrt{\mathrm{tan}\:^{\mathrm{2}} \alpha\left(\mathrm{tan}\:\beta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{tan}\:^{\mathrm{2}} \beta\left(\mathrm{tan}\:\alpha−\mathrm{1}\right)^{\mathrm{2}} }}\: \\ $$$$\frac{{c}}{\mathrm{cos}\:\theta}=\frac{\mathrm{1}}{\mathrm{sin}\:\beta} \\ $$$$\boldsymbol{{c}}\:=\:\frac{\mathrm{cos}\:\boldsymbol{\beta}\left(\mathrm{tan}\:\alpha−\mathrm{1}\right)}{\:\sqrt{\mathrm{tan}\:^{\mathrm{2}} \alpha\left(\mathrm{tan}\:\beta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{tan}\:^{\mathrm{2}} \beta\left(\mathrm{tan}\:\alpha−\mathrm{1}\right)^{\mathrm{2}} }}\: \\ $$$$…. \\ $$
Commented by MrW3 last updated on 16/Jul/18
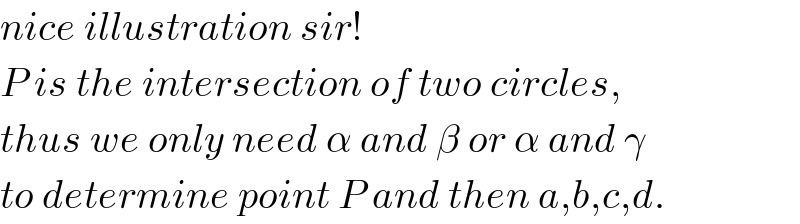
nice illustration sir! P is the intersection of two circles, thus we only need α and β or α and γ to determine point P and then a,b,c,d.
$${nice}\:{illustration}\:{sir}! \\ $$$${P}\:{is}\:{the}\:{intersection}\:{of}\:{two}\:{circles}, \\ $$$${thus}\:{we}\:{only}\:{need}\:\alpha\:{and}\:\beta\:{or}\:\alpha\:{and}\:\gamma \\ $$$${to}\:{determine}\:{point}\:{P}\:{and}\:{then}\:{a},{b},{c},{d}. \\ $$
Answered by MrW3 last updated on 16/Jul/18
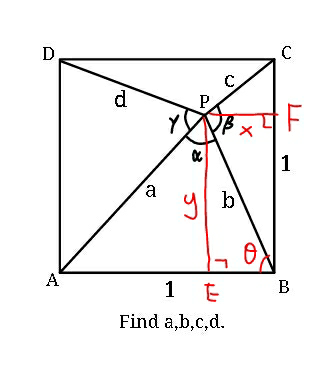
Commented by MrW3 last updated on 17/Jul/18
(1/(sin α))=(b/(sin (α+θ))) ⇒b=((sin (α+θ))/(sin α))=cos θ+((sin θ)/(tan α)) (1/(sin β))=(b/(sin (β+(π/2)−θ))) ⇒b=((sin [(π/2)−(θ−β)])/(sin β))=((cos (θ−β))/(sin β))=((cos θ)/(tan β))+sin θ cos θ+((sin θ)/(tan α))=((cos θ)/(tan β))+sin θ tan β (1−tan α) sin θ=tan α (1−tan β) cos θ ⇒tan θ=((tan α (1−tan β))/(tan β (1−tan α)))=((1−cot β)/(1−cot α)) ⇒sin θ=((1−cot β)/( (√((1−cot α)^2 +(1−cot β)^2 )))) ⇒cos θ=((1−cot α)/( (√((1−cot α)^2 +(1−cot β)^2 )))) ⇒θ=tan^(−1) ((1−cot β)/(1−cot α)) (a/(sin θ))=(1/(sin α)) ⇒a=((sin θ)/(sin α)) ⇒a=((1−cot β)/(sin α (√((1−cot α)^2 +(1−cot β)^2 )))) b=cos θ+((sin θ)/(tan α)) ⇒b=((1−cot α cot β)/( (√((1−cot α)^2 +(1−cot β)^2 )))) (c/(sin ((π/2)−θ)))=(1/(sin β)) ⇒c=((cos θ)/(sin β)) ⇒c=((1−cot α)/(sin β (√((1−cot α)^2 +(1−cot β)^2 )))) ⇒d=((1−cot α)/(sin γ (√((1−cot γ)^2 +(1−cot α)^2 )))) but d can also be expressed without γ: ⇒x=b cos θ ⇒y=b sin θ ⇒d=(√((1−x)^2 +(1−y)^2 )) =(√(2+x^2 +y^2 −2(x+y))) =(√(2+b^2 −2b(cos θ+sin θ))) ⇒d=(√(2+(((1−cot α cot β)[5−2(cot α+cot β)])/((1−cot α)^2 +(1−cot β)^2 )))) i.e. we only need two parameters from α,β,γ to determine a,b,c,d.
$$\frac{\mathrm{1}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\left(\alpha+\theta\right)} \\ $$$$\Rightarrow{b}=\frac{\mathrm{sin}\:\left(\alpha+\theta\right)}{\mathrm{sin}\:\alpha}=\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\beta}=\frac{{b}}{\mathrm{sin}\:\left(\beta+\frac{\pi}{\mathrm{2}}−\theta\right)} \\ $$$$\Rightarrow{b}=\frac{\mathrm{sin}\:\left[\frac{\pi}{\mathrm{2}}−\left(\theta−\beta\right)\right]}{\mathrm{sin}\:\beta}=\frac{\mathrm{cos}\:\left(\theta−\beta\right)}{\mathrm{sin}\:\beta}=\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}+\mathrm{sin}\:\theta \\ $$$$\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha}=\frac{\mathrm{cos}\:\theta}{\mathrm{tan}\:\beta}+\mathrm{sin}\:\theta \\ $$$$\mathrm{tan}\:\beta\:\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)\:\mathrm{sin}\:\theta=\mathrm{tan}\:\alpha\:\left(\mathrm{1}−\mathrm{tan}\:\beta\right)\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{tan}\:\alpha\:\left(\mathrm{1}−\mathrm{tan}\:\beta\right)}{\mathrm{tan}\:\beta\:\left(\mathrm{1}−\mathrm{tan}\:\alpha\right)}=\frac{\mathrm{1}−\mathrm{cot}\:\beta}{\mathrm{1}−\mathrm{cot}\:\alpha} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{1}−\mathrm{cot}\:\beta}{\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}−\mathrm{cot}\:\alpha}{\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−\mathrm{cot}\:\beta}{\mathrm{1}−\mathrm{cot}\:\alpha} \\ $$$$\frac{{a}}{\mathrm{sin}\:\theta}=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow{a}=\frac{\mathrm{sin}\:\theta}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}−\mathrm{cot}\:\beta}{\mathrm{sin}\:\alpha\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$${b}=\mathrm{cos}\:\theta+\frac{\mathrm{sin}\:\theta}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}−\mathrm{cot}\:\alpha\:\mathrm{cot}\:\beta}{\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$$\frac{{c}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\beta} \\ $$$$\Rightarrow{c}=\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\beta} \\ $$$$\Rightarrow{c}=\frac{\mathrm{1}−\mathrm{cot}\:\alpha}{\mathrm{sin}\:\beta\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{d}=\frac{\mathrm{1}−\mathrm{cot}\:\alpha}{\mathrm{sin}\:\gamma\:\sqrt{\left(\mathrm{1}−\mathrm{cot}\:\gamma\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$${but}\:{d}\:{can}\:{also}\:{be}\:{expressed}\:{without}\:\gamma: \\ $$$$\Rightarrow{x}={b}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{y}={b}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{d}=\sqrt{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left(\mathrm{1}−{y}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{2}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}\left({x}+{y}\right)} \\ $$$$=\sqrt{\mathrm{2}+{b}^{\mathrm{2}} −\mathrm{2}{b}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)} \\ $$$$\Rightarrow{d}=\sqrt{\mathrm{2}+\frac{\left(\mathrm{1}−\mathrm{cot}\:\alpha\:\mathrm{cot}\:\beta\right)\left[\mathrm{5}−\mathrm{2}\left(\mathrm{cot}\:\alpha+\mathrm{cot}\:\beta\right)\right]}{\left(\mathrm{1}−\mathrm{cot}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{cot}\:\beta\right)^{\mathrm{2}} }} \\ $$$${i}.{e}.\:{we}\:{only}\:{need}\:{two}\:{parameters}\:{from} \\ $$$$\alpha,\beta,\gamma\:{to}\:{determine}\:{a},{b},{c},{d}. \\ $$
Commented by ajfour last updated on 16/Jul/18
Very enlightening Sir!
$${Very}\:{enlightening}\:{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *