Question Number 40173 by scientist last updated on 16/Jul/18
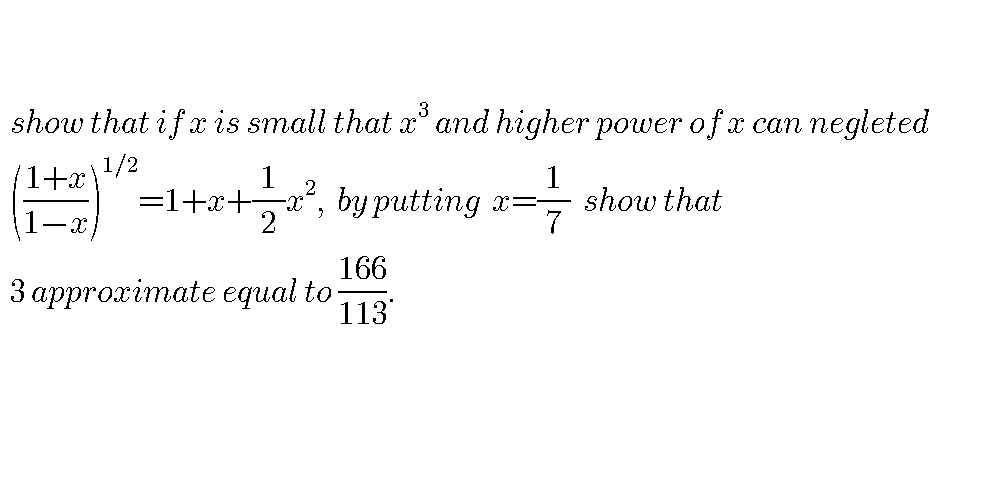
Commented by math khazana by abdo last updated on 17/Jul/18
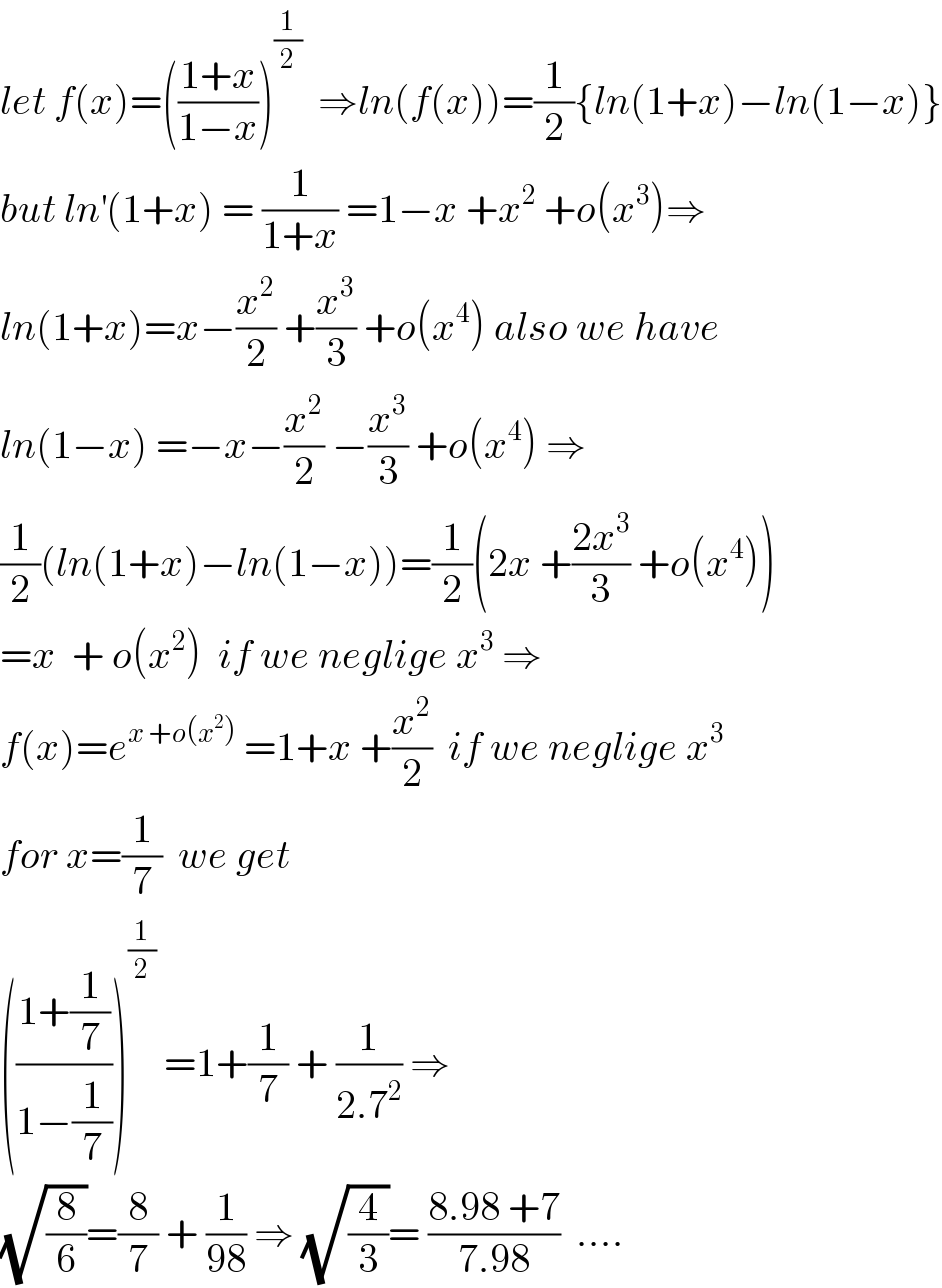
$${let}\:{f}\left({x}\right)=\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\Rightarrow{ln}\left({f}\left({x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\right\} \\ $$$${but}\:{ln}^{'} \left(\mathrm{1}+{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\mathrm{1}−{x}\:+{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{3}} \right)\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{4}} \right)\:{also}\:{we}\:{have} \\ $$$${ln}\left(\mathrm{1}−{x}\right)\:=−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}\:+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{3}}\:+{o}\left({x}^{\mathrm{4}} \right)\right) \\ $$$$={x}\:\:+\:{o}\left({x}^{\mathrm{2}} \right)\:\:{if}\:{we}\:{neglige}\:{x}^{\mathrm{3}} \:\Rightarrow \\ $$$${f}\left({x}\right)={e}^{{x}\:+{o}\left({x}^{\mathrm{2}} \right)} \:=\mathrm{1}+{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:{if}\:{we}\:{neglige}\:{x}^{\mathrm{3}} \\ $$$${for}\:{x}=\frac{\mathrm{1}}{\mathrm{7}}\:\:{we}\:{get} \\ $$$$\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{2}.\mathrm{7}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sqrt{\frac{\mathrm{8}}{\mathrm{6}}}=\frac{\mathrm{8}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{98}}\:\Rightarrow\:\sqrt{\frac{\mathrm{4}}{\mathrm{3}}}=\:\frac{\mathrm{8}.\mathrm{98}\:+\mathrm{7}}{\mathrm{7}.\mathrm{98}}\:\:…. \\ $$
Answered by MJS last updated on 16/Jul/18

$$\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}+{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$$\mathrm{1}+{x}=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{1}+{x}=\mathrm{1}+{x}−\left({x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{5}} \right) \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{ignore}\:{x}^{{n}} \:\mathrm{with}\:{n}\geqslant\mathrm{3}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\approx\mathrm{1}.\mathrm{15470} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }=\frac{\mathrm{113}}{\mathrm{98}}\approx\mathrm{1}.\mathrm{15306} \\ $$$$\mathrm{the}\:\mathrm{mistake}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{610}}\:\mathrm{or}\:\mathrm{0}.\mathrm{14\%} \\ $$$$\left(\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{where}\:\frac{\mathrm{166}}{\mathrm{113}}\:\mathrm{comes}\:\mathrm{from}\right) \\ $$
