Question Number 40277 by Raj Singh last updated on 18/Jul/18

Answered by MJS last updated on 18/Jul/18
![(d/dθ)[sin^p θ cos^q θ]=sin^(p−1) θ cos^(q−1) θ (pcos^2 θ −qsin^2 θ) zeros at sin θ =0 ⇒ θ=2nπ cos θ =0 ⇒ θ=(2n+1)(π/2) pcos^2 θ −qsin^2 θ =0 pc^2 −qs^2 =0 p(1−s^2 )−qs^2 =0 p−ps^2 −qs^2 =0 sin^2 θ =(p/(p+q)) ⇒ cos^2 θ =1−(p/(p+q))=(q/(p+q)) ⇒ tan^2 θ =(p/q) ⇒ θ=arctan (√(p/q))](https://www.tinkutara.com/question/Q40281.png)
$$\frac{{d}}{{d}\theta}\left[\mathrm{sin}^{{p}} \:\theta\:\mathrm{cos}^{{q}} \:\theta\right]=\mathrm{sin}^{{p}−\mathrm{1}} \:\theta\:\mathrm{cos}^{{q}−\mathrm{1}} \:\theta\:\left({p}\mathrm{cos}^{\mathrm{2}} \:\theta\:−{q}\mathrm{sin}^{\mathrm{2}} \:\theta\right) \\ $$$$\mathrm{zeros}\:\mathrm{at} \\ $$$$\mathrm{sin}\:\theta\:=\mathrm{0}\:\Rightarrow\:\theta=\mathrm{2}{n}\pi \\ $$$$\mathrm{cos}\:\theta\:=\mathrm{0}\:\Rightarrow\:\theta=\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$${p}\mathrm{cos}^{\mathrm{2}} \:\theta\:−{q}\mathrm{sin}^{\mathrm{2}} \:\theta\:=\mathrm{0} \\ $$$${pc}^{\mathrm{2}} −{qs}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}\left(\mathrm{1}−{s}^{\mathrm{2}} \right)−{qs}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}−{ps}^{\mathrm{2}} −{qs}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta\:=\frac{{p}}{{p}+{q}} \\ $$$$\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \:\theta\:=\mathrm{1}−\frac{{p}}{{p}+{q}}=\frac{{q}}{{p}+{q}} \\ $$$$\Rightarrow\:\mathrm{tan}^{\mathrm{2}} \:\theta\:=\frac{{p}}{{q}} \\ $$$$\Rightarrow\:\theta=\mathrm{arctan}\:\sqrt{\frac{{p}}{{q}}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jul/18
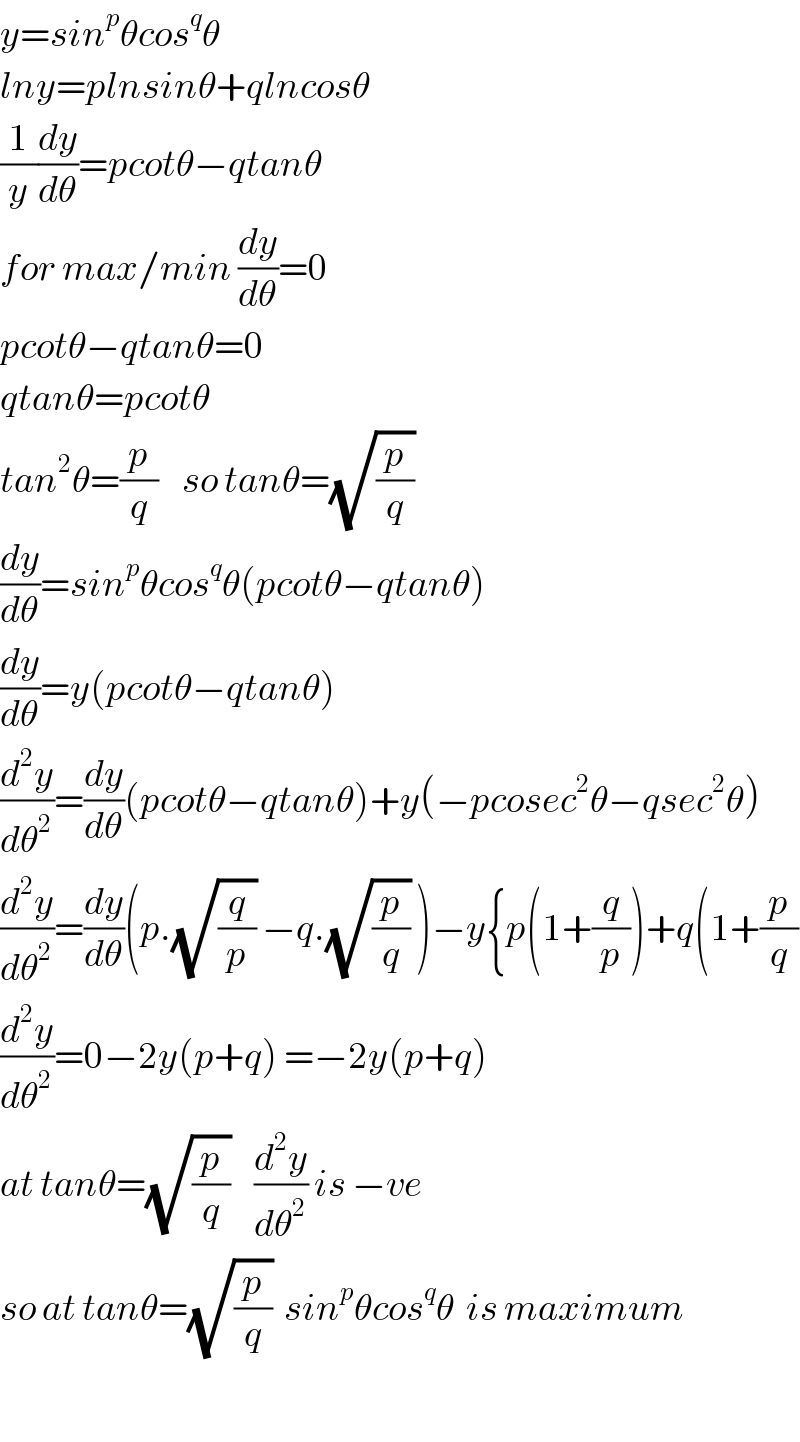
$${y}={sin}^{{p}} \theta{cos}^{{q}} \theta \\ $$$${lny}={plnsin}\theta+{qlncos}\theta \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{d}\theta}={pcot}\theta−{qtan}\theta \\ $$$${for}\:{max}/{min}\:\frac{{dy}}{{d}\theta}=\mathrm{0} \\ $$$${pcot}\theta−{qtan}\theta=\mathrm{0} \\ $$$${qtan}\theta={pcot}\theta \\ $$$${tan}^{\mathrm{2}} \theta=\frac{{p}}{{q}}\:\:\:\:{so}\:{tan}\theta=\sqrt{\frac{{p}}{{q}}} \\ $$$$\frac{{dy}}{{d}\theta}={sin}^{{p}} \theta{cos}^{{q}} \theta\left({pcot}\theta−{qtan}\theta\right) \\ $$$$\frac{{dy}}{{d}\theta}={y}\left({pcot}\theta−{qtan}\theta\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{d}\theta^{\mathrm{2}} }=\frac{{dy}}{{d}\theta}\left({pcot}\theta−{qtan}\theta\right)+{y}\left(−{pcosec}^{\mathrm{2}} \theta−{qsec}^{\mathrm{2}} \theta\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{d}\theta^{\mathrm{2}} }=\frac{{dy}}{{d}\theta}\left({p}.\sqrt{\frac{{q}}{{p}}}\:−{q}.\sqrt{\frac{{p}}{{q}}}\:\right)−{y}\left\{{p}\left(\mathrm{1}+\frac{{q}}{{p}}\right)+{q}\left(\mathrm{1}+\frac{{p}}{{q}}\right.\right. \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{d}\theta^{\mathrm{2}} }=\mathrm{0}−\mathrm{2}{y}\left({p}+{q}\right)\:=−\mathrm{2}{y}\left({p}+{q}\right) \\ $$$${at}\:{tan}\theta=\sqrt{\frac{{p}}{{q}}}\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{d}\theta^{\mathrm{2}} }\:{is}\:−{ve} \\ $$$${so}\:{at}\:{tan}\theta=\sqrt{\frac{{p}}{{q}}}\:\:{sin}^{{p}} \theta{cos}^{{q}} \theta\:\:{is}\:{maximum} \\ $$$$ \\ $$
