Question Number 40344 by behi83417@gmail.com last updated on 20/Jul/18
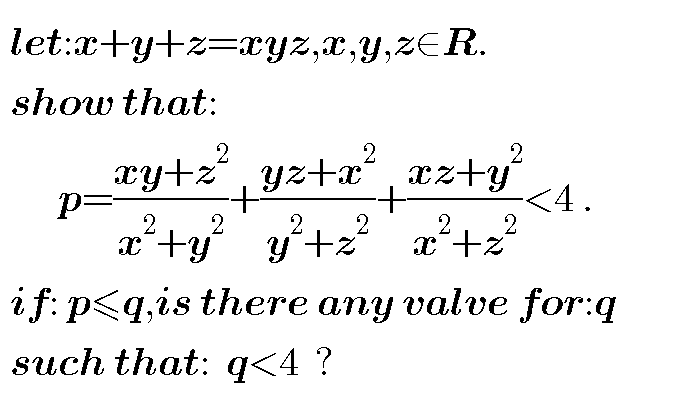
Commented by MJS last updated on 20/Jul/18
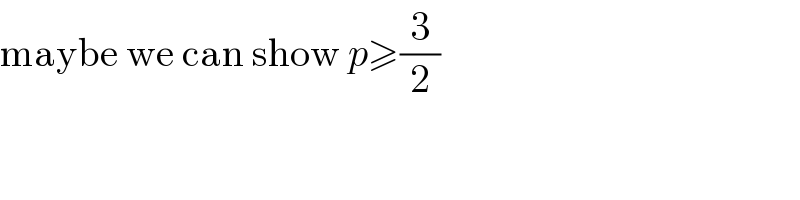
$$\mathrm{maybe}\:\mathrm{we}\:\mathrm{can}\:\mathrm{show}\:{p}\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 21/Jul/18
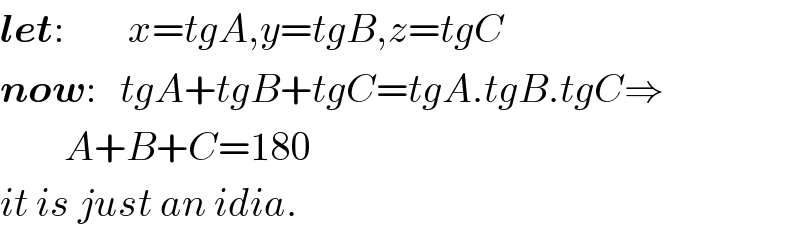
$$\boldsymbol{{let}}:\:\:\:\:\:\:\:\:{x}={tgA},{y}={tgB},{z}={tgC} \\ $$$$\boldsymbol{{now}}:\:\:\:{tgA}+{tgB}+{tgC}={tgA}.{tgB}.{tgC}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:{A}+{B}+{C}=\mathrm{180} \\ $$$${it}\:{is}\:{just}\:{an}\:{idia}. \\ $$
Answered by MJS last updated on 20/Jul/18

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{true} \\ $$$${x}=\mathrm{1} \\ $$$${y}=\mathrm{4} \\ $$$${z}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${p}=\frac{\mathrm{283571}}{\mathrm{51714}}>\mathrm{4} \\ $$
Commented by behi83417@gmail.com last updated on 20/Jul/18
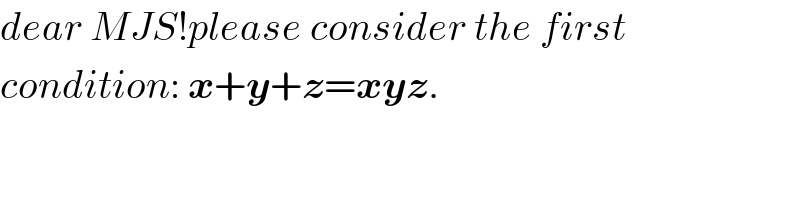
$${dear}\:{MJS}!{please}\:{consider}\:{the}\:{first} \\ $$$${condition}:\:\boldsymbol{{x}}+\boldsymbol{{y}}+\boldsymbol{{z}}=\boldsymbol{{xyz}}. \\ $$
Commented by MJS last updated on 20/Jul/18

$$\mathrm{I}\:\mathrm{did}: \\ $$$$\mathrm{1}+\mathrm{4}+\frac{\mathrm{5}}{\mathrm{3}}=\frac{\mathrm{20}}{\mathrm{3}} \\ $$$$\mathrm{1}×\mathrm{4}×\frac{\mathrm{5}}{\mathrm{3}}=\frac{\mathrm{20}}{\mathrm{3}} \\ $$
Commented by MrW3 last updated on 20/Jul/18

$${x}+{y}+{z}={xyz} \\ $$$$\Rightarrow{z}=\frac{{x}+{y}}{{xy}−\mathrm{1}} \\ $$$${p}=…={F}\left({x},{y}\right) \\ $$$${F}\left({x},{y}\right)\:{has}\:{no}\:{maxima}. \\ $$$${p}={F}\left(\mathrm{1},\mathrm{4}\right)\:=\mathrm{5}.\mathrm{48}…>\mathrm{4} \\ $$$${p}={F}\left(\mathrm{1},\mathrm{100}\right)=\mathrm{4900}.\mathrm{5}…>\mathrm{4} \\ $$$${p}={F}\left(\mathrm{1},\mathrm{1000}\right)=\mathrm{499000}.\mathrm{5}…>\mathrm{4} \\ $$$$ \\ $$$${statement}\:{that}\:{p}<{q}\:\left(=\mathrm{4}\:{or}\:{what}\:{ever}\right) \\ $$$${is}\:{not}\:{true}. \\ $$
