Question Number 40376 by behi83417@gmail.com last updated on 21/Jul/18
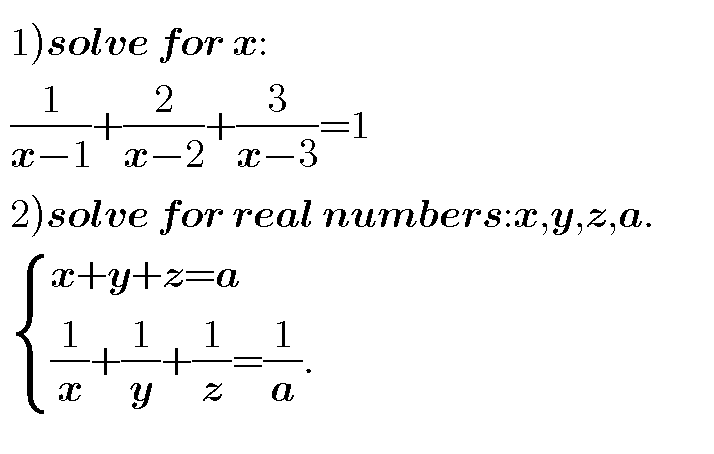
Commented by MrW3 last updated on 21/Jul/18

$$\left(\mathrm{1}\right) \\ $$$${let}\:{u}={x}−\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{u}+\mathrm{1}}+\frac{\mathrm{3}}{{u}−\mathrm{1}}=\mathrm{1}−\frac{\mathrm{2}}{{u}} \\ $$$$\frac{\mathrm{4}{u}+\mathrm{2}}{{u}^{\mathrm{2}} −\mathrm{1}}=\frac{{u}−\mathrm{2}}{{u}} \\ $$$$\mathrm{4}{u}^{\mathrm{2}} +\mathrm{2}{u}={u}^{\mathrm{3}} −{u}−\mathrm{2}{u}^{\mathrm{2}} +\mathrm{2} \\ $$$${u}^{\mathrm{3}} −\mathrm{6}{u}^{\mathrm{2}} −\mathrm{3}{u}+\mathrm{2}=\mathrm{0} \\ $$$${u}={x}−\mathrm{2}=−\mathrm{0}.\mathrm{8056},\:\mathrm{0}.\mathrm{3868},\:\mathrm{6}.\mathrm{4188} \\ $$$$\Rightarrow{x}=\mathrm{1}.\mathrm{1944},\:\mathrm{2}.\mathrm{3868},\:\mathrm{8}.\mathrm{4188} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${solution}\:{is}: \\ $$$${one}\:{of}\:{the}\:{three}\:{variables}\:{is}\:{a},\:{the} \\ $$$${other}\:{two}\:{can}\:{be}\:{any}\:{value}\:{but}\:{with} \\ $$$${different}\:+\:{and}\:−\:{sign},\:{e}.{g}. \\ $$$$\begin{cases}{{x}={r}={any}\:{real}\:{number}}\\{{y}=−{r}}\\{{z}={a}}\end{cases} \\ $$
Commented by behi83417@gmail.com last updated on 21/Jul/18
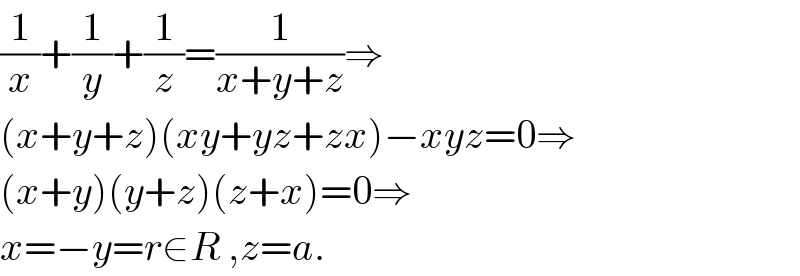
$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{x}+{y}+{z}}\Rightarrow \\ $$$$\left({x}+{y}+{z}\right)\left({xy}+{yz}+{zx}\right)−{xyz}=\mathrm{0}\Rightarrow \\ $$$$\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)=\mathrm{0}\Rightarrow \\ $$$${x}=−{y}={r}\in{R}\:,{z}={a}. \\ $$
Commented by behi83417@gmail.com last updated on 21/Jul/18
$${thanks}\:{in}\:{advance}\:{dear}\:{master}. \\ $$
