Question-40469

Question Number 40469 by MrW3 last updated on 22/Jul/18

Commented by MrW3 last updated on 22/Jul/18

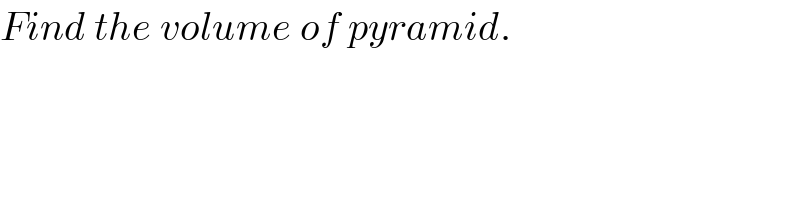
$${Find}\:{the}\:{volume}\:{of}\:{pyramid}. \\ $$

Commented by MJS last updated on 22/Jul/18

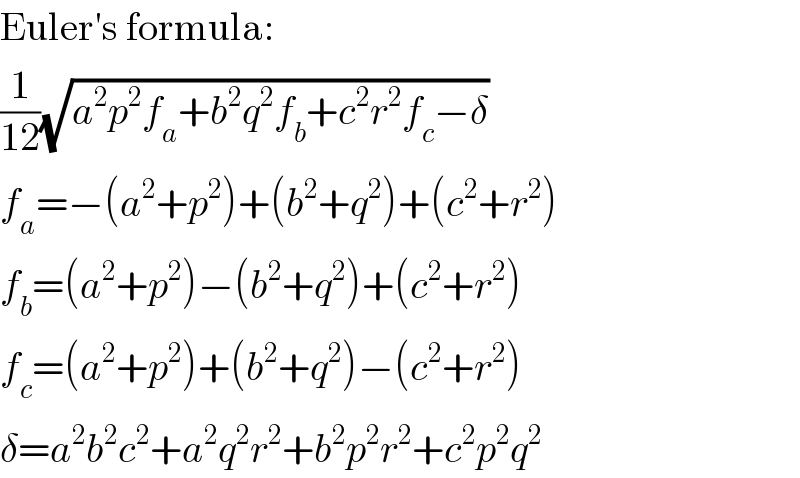
Euler′s formula: (1/(12))(√(a^2 p^2 f_a +b^2 q^2 f_b +c^2 r^2 f_c −δ)) f_a =−(a^2 +p^2 )+(b^2 +q^2 )+(c^2 +r^2 ) f_b =(a^2 +p^2 )−(b^2 +q^2 )+(c^2 +r^2 ) f_c =(a^2 +p^2 )+(b^2 +q^2 )−(c^2 +r^2 ) δ=a^2 b^2 c^2 +a^2 q^2 r^2 +b^2 p^2 r^2 +c^2 p^2 q^2

$$\mathrm{Euler}'\mathrm{s}\:\mathrm{formula}: \\ $$$$\frac{\mathrm{1}}{\mathrm{12}}\sqrt{{a}^{\mathrm{2}} {p}^{\mathrm{2}} {f}_{{a}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} {f}_{{b}} +{c}^{\mathrm{2}} {r}^{\mathrm{2}} {f}_{{c}} −\delta} \\ $$$${f}_{{a}} =−\left({a}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)+\left({b}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+\left({c}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$${f}_{{b}} =\left({a}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)−\left({b}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+\left({c}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$${f}_{{c}} =\left({a}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)+\left({b}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−\left({c}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\delta={a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} +{b}^{\mathrm{2}} {p}^{\mathrm{2}} {r}^{\mathrm{2}} +{c}^{\mathrm{2}} {p}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$

Commented by MrW3 last updated on 22/Jul/18

$${thank}\:{you}\:{sir}! \\ $$

Commented by MJS last updated on 22/Jul/18

there′s also a matrix−formula for a simplex in R^n (in R^1 the simplex is a line segment, in R^2 a triangle and in R^3 a tetrahedron, the Euler−formula for R^2 is the same as Heron′s A_(△abc) =(1/4)(√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))) but I couldn′t find this matrix...

$$\mathrm{there}'\mathrm{s}\:\mathrm{also}\:\mathrm{a}\:\mathrm{matrix}−\mathrm{formula}\:\mathrm{for}\:\mathrm{a}\:\mathrm{simplex} \\ $$$$\mathrm{in}\:\mathbb{R}^{{n}} \:\left(\mathrm{in}\:\mathbb{R}^{\mathrm{1}} \:\mathrm{the}\:\mathrm{simplex}\:\mathrm{is}\:\mathrm{a}\:\mathrm{line}\:\mathrm{segment},\:\mathrm{in}\right. \\ $$$$\mathbb{R}^{\mathrm{2}} \:\mathrm{a}\:\mathrm{triangle}\:\mathrm{and}\:\mathrm{in}\:\mathbb{R}^{\mathrm{3}} \:\mathrm{a}\:\mathrm{tetrahedron},\:\mathrm{the} \\ $$$$\mathrm{Euler}−\mathrm{formula}\:\mathrm{for}\:\mathbb{R}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{Heron}'\mathrm{s} \\ $$$$\left.{A}_{\bigtriangleup{abc}} =\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}\right) \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{couldn}'\mathrm{t}\:\mathrm{find}\:\mathrm{this}\:\mathrm{matrix}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply