Menu Close

Question-40551

Tinku Tara 0 Comments
Pin




Question Number 40551 by ajfour last updated on 24/Jul/18
Commented by ajfour last updated on 24/Jul/18
A chain of mass m, length l hangs the table edge only as much so that it just starts slipping down. Friction coefficient between chain and table being 𝛍. Find speed of chain as end B of chain reaches the table corner.
$${A}\:{chain}\:{of}\:{mass}\:\boldsymbol{{m}},\:{length}\:\boldsymbol{{l}} \\ $$$${hangs}\:{the}\:{table}\:{edge}\:{only}\:{as}\:{much} \\ $$$${so}\:{that}\:{it}\:{just}\:{starts}\:{slipping} \\ $$$${down}.\:{Friction}\:{coefficient}\: \\ $$$${between}\:{chain}\:{and}\:{table}\:{being}\:\boldsymbol{\mu}. \\ $$$${Find}\:{speed}\:{of}\:{chain}\:{as}\:{end}\:{B}\:{of} \\ $$$${chain}\:{reaches}\:{the}\:{table}\:{corner}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Jul/18
let when time=t y length of chain suspended l−y length on the tablle so wt of hanging chain is (m/l)yg↓ force on chain on table are 1)(m/l)(l−y)g↓ 2)friction μ((m/l))(l−y)g 3)forward force which cause the chain to move=(m/l)yg so acc=(((m/l)yg−μ((m/l))(l−y)g)/m)=v(dv/dy) (g/l)y−((μg)/l)(l−y)=v(dv/dy) ∫(g/l)ydy−∫μgdy+((μg)/l)∫ydy=∫vdv now initial suspended lenth of chain say y_0 so as per question (m/l)y_0 g=μ(m/l)(l−y_0 )g y_0 =μ(l−y_0 ) y_0 =((μl)/(1+μ)) wait i am intregating... (g/l)∫_((μl)/(1+μ)) ^l ydy −μg∫_((μl)/(1+μ)) ^l dy+((μg)/l)∫_((μl)/(1+μ)) ^l ydy=∫_0 ^v vdv (g/(2l))∣(y^2 )∣_((μl)/(1+μ)) ^l −μg(l−((μl)/(1+μ)))+((μg)/(2l)){(l^2 −(((μl)/(1+μ)))^2 }=(v^2 /2) (g/(2l)){l^2 −((μ^2 l^2 )/((1+μ)^2 ))}−μg((l/(1+μ)))+((μg)/(2l)){l^2 −((μ^2 l^2 )/((1+μ)^2 ))} (g/(2l))(1+μ)l^2 (((1+2μ+μ^2 −μ^2 )/((1+μ)^2 )))−μg((l/(1+μ)))=(v^2 /2) (g/(2l))l^2 (((1+2μ)/(1+μ)))−μg((l/(1+μ)))=(v^2 /2) ((gl(((1+2μ)/(1+μ)))−2μg((l/(1+μ)))=v^2 )/) ((gl+2μgl−2μgl)/(1+μ))=v^2 v=(√((gl)/(1+μ))) pls check...
$${let}\:{when}\:{time}={t}\:\:\:\:{y}\:{length}\:{of}\:{chain}\:{suspended} \\ $$$${l}−{y}\:\:{length}\:{on}\:{the}\:{tablle} \\ $$$${so}\:{wt}\:{of}\:{hanging}\:{chain}\:{is}\:\frac{{m}}{{l}}{yg}\downarrow \\ $$$${force}\:{on}\:{chain}\:{on}\:{table}\:\:{are} \\ $$$$\left.\mathrm{1}\right)\frac{{m}}{{l}}\left({l}−{y}\right){g}\downarrow \\ $$$$\left.\mathrm{2}\right){friction}\:\mu\left(\frac{{m}}{{l}}\right)\left({l}−{y}\right){g} \\ $$$$\left.\mathrm{3}\right){forward}\:{force}\:{which}\:{cause}\:{the}\:{chain}\:{to}\: \\ $$$${move}=\frac{{m}}{{l}}{yg} \\ $$$${so}\:{acc}=\frac{\frac{{m}}{{l}}{yg}−\mu\left(\frac{{m}}{{l}}\right)\left({l}−{y}\right){g}}{{m}}={v}\frac{{dv}}{{dy}} \\ $$$$\frac{{g}}{{l}}{y}−\frac{\mu{g}}{{l}}\left({l}−{y}\right)={v}\frac{{dv}}{{dy}} \\ $$$$\int\frac{{g}}{{l}}{ydy}−\int\mu{gdy}+\frac{\mu{g}}{{l}}\int{ydy}=\int{vdv} \\ $$$${now}\:{initial}\:{suspended}\:{lenth}\:{of}\:{chain}\:{say}\:{y}_{\mathrm{0}} \\ $$$${so}\:{as}\:{per}\:{question} \\ $$$$\frac{{m}}{{l}}{y}_{\mathrm{0}} {g}=\mu\frac{{m}}{{l}}\left({l}−{y}_{\mathrm{0}} \right){g} \\ $$$${y}_{\mathrm{0}} =\mu\left({l}−{y}_{\mathrm{0}} \right) \\ $$$${y}_{\mathrm{0}} =\frac{\mu{l}}{\mathrm{1}+\mu} \\ $$$${wait}\:{i}\:{am}\:{intregating}… \\ $$$$\frac{{g}}{{l}}\int_{\frac{\mu{l}}{\mathrm{1}+\mu}} ^{{l}} {ydy}\:\:−\mu{g}\int_{\frac{\mu{l}}{\mathrm{1}+\mu}} ^{{l}} {dy}+\frac{\mu{g}}{{l}}\int_{\frac{\mu{l}}{\mathrm{1}+\mu}} ^{{l}} {ydy}=\int_{\mathrm{0}} ^{{v}} {vdv} \\ $$$$\frac{{g}}{\mathrm{2}{l}}\mid\left({y}^{\mathrm{2}} \right)\mid_{\frac{\mu{l}}{\mathrm{1}+\mu}} ^{{l}} −\mu{g}\left({l}−\frac{\mu{l}}{\mathrm{1}+\mu}\right)+\frac{\mu{g}}{\mathrm{2}{l}}\left\{\left({l}^{\mathrm{2}} −\left(\frac{\mu{l}}{\mathrm{1}+\mu}\right)^{\mathrm{2}} \right\}=\frac{{v}^{\mathrm{2}} }{\mathrm{2}}\right. \\ $$$$\frac{{g}}{\mathrm{2}{l}}\left\{{l}^{\mathrm{2}} −\frac{\mu^{\mathrm{2}} {l}^{\mathrm{2}} }{\left(\mathrm{1}+\mu\right)^{\mathrm{2}} }\right\}−\mu{g}\left(\frac{{l}}{\mathrm{1}+\mu}\right)+\frac{\mu{g}}{\mathrm{2}{l}}\left\{{l}^{\mathrm{2}} −\frac{\mu^{\mathrm{2}} {l}^{\mathrm{2}} }{\left(\mathrm{1}+\mu\right)^{\mathrm{2}} }\right\} \\ $$$$\frac{{g}}{\mathrm{2}{l}}\left(\mathrm{1}+\mu\right){l}^{\mathrm{2}} \left(\frac{\mathrm{1}+\mathrm{2}\mu+\mu^{\mathrm{2}} −\mu^{\mathrm{2}} }{\left(\mathrm{1}+\mu\right)^{\mathrm{2}} }\right)−\mu{g}\left(\frac{{l}}{\mathrm{1}+\mu}\right)=\frac{{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{g}}{\mathrm{2}{l}}{l}^{\mathrm{2}} \left(\frac{\mathrm{1}+\mathrm{2}\mu}{\mathrm{1}+\mu}\right)−\mu{g}\left(\frac{{l}}{\mathrm{1}+\mu}\right)=\frac{{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{gl}\left(\frac{\mathrm{1}+\mathrm{2}\mu}{\mathrm{1}+\mu}\right)−\mathrm{2}\mu{g}\left(\frac{{l}}{\mathrm{1}+\mu}\right)={v}^{\mathrm{2}} }{} \\ $$$$\frac{{gl}+\mathrm{2}\mu{gl}−\mathrm{2}\mu{gl}}{\mathrm{1}+\mu}={v}^{\mathrm{2}} \\ $$$${v}=\sqrt{\frac{{gl}}{\mathrm{1}+\mu}}\:\:{pls}\:{check}… \\ $$
Commented by ajfour last updated on 24/Jul/18
Thank you Tanmay Sir; but mrW sir has solved it beautifully.
$${Thank}\:{you}\:{Tanmay}\:{Sir};\:{but}\:{mrW} \\ $$$${sir}\:{has}\:{solved}\:{it}\:{beautifully}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Jul/18
yes you are right...ihave reached destination but along the long path...
$${yes}\:{you}\:{are}\:{right}…{ihave}\:{reached}\:{destination} \\ $$$${but}\:{along}\:{the}\:{long}\:{path}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Jul/18
i have put the value of y_0 early...MWr_3 put the value in the final stage and i have calculated mass of chain by (m/(l )) factor so in calculation it takes time...but he put simply ρ=(m/l) again put the value of ρ in final stage...
$${i}\:{have}\:{put}\:{the}\:{value}\:{of}\:{y}_{\mathrm{0}} \:{early}…{MWr}_{\mathrm{3}} \:{put}\:{the} \\ $$$${value}\:{in}\:{the}\:{final}\:{stage}\:{and}\:{i}\:{have}\:{calculated} \\ $$$${mass}\:{of}\:{chain}\:{by}\:\frac{{m}}{{l}\:}\:{factor}\:{so}\:{in}\:{calculation} \\ $$$${it}\:{takes}\:{time}…{but}\:{he}\:{put}\:{simply}\:\rho=\frac{{m}}{{l}} \\ $$$${again}\:{put}\:{the}\:{value}\:{of}\:\rho\:{in}\:{final}\:{stage}… \\ $$
Answered by MrW3 last updated on 24/Jul/18
length of hanging part=y ρ=(m/l) y_0 ρg=μ(l−y_0 )ρg ⇒y_0 =(μ/(1+μ)) l yρg−μ(l−y)ρg=ma=lρ v(dv/dy) y−μ(l−y)=(l/g) v(dv/dy) ∫_y_0 ^l [(1+μ)y−μl]dy=(l/g) ∫_0 ^v vdv [(1+μ)(y^2 /2)−μly]_y_0 ^l =(l/g) (v^2 /2) (1/2)(1+μ)(l^2 −y_0 ^2 )−μl(l−y_0 )=(l/g) (v^2 /2) [(1+μ)(l+y_0 )−2μl](l−y_0 )=(l/g) v^2 [(1+μ)(1+(μ/(1+μ)))−2μ](1−(μ/(1+μ)))lg=v^2 ((lg)/(1+μ))=v^2 ⇒v=(√((lg)/(1+μ)))
$${length}\:{of}\:{hanging}\:{part}={y} \\ $$$$\rho=\frac{{m}}{{l}} \\ $$$${y}_{\mathrm{0}} \rho{g}=\mu\left({l}−{y}_{\mathrm{0}} \right)\rho{g} \\ $$$$\Rightarrow{y}_{\mathrm{0}} =\frac{\mu}{\mathrm{1}+\mu}\:{l} \\ $$$${y}\rho{g}−\mu\left({l}−{y}\right)\rho{g}={ma}={l}\rho\:{v}\frac{{dv}}{{dy}} \\ $$$${y}−\mu\left({l}−{y}\right)=\frac{{l}}{{g}}\:{v}\frac{{dv}}{{dy}} \\ $$$$\int_{{y}_{\mathrm{0}} } ^{{l}} \left[\left(\mathrm{1}+\mu\right){y}−\mu{l}\right]{dy}=\frac{{l}}{{g}}\:\int_{\mathrm{0}} ^{{v}} {vdv} \\ $$$$\left[\left(\mathrm{1}+\mu\right)\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−\mu{ly}\right]_{{y}_{\mathrm{0}} } ^{{l}} =\frac{{l}}{{g}}\:\frac{{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mu\right)\left({l}^{\mathrm{2}} −{y}_{\mathrm{0}} ^{\mathrm{2}} \right)−\mu{l}\left({l}−{y}_{\mathrm{0}} \right)=\frac{{l}}{{g}}\:\frac{{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left[\left(\mathrm{1}+\mu\right)\left({l}+{y}_{\mathrm{0}} \right)−\mathrm{2}\mu{l}\right]\left({l}−{y}_{\mathrm{0}} \right)=\frac{{l}}{{g}}\:{v}^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{1}+\mu\right)\left(\mathrm{1}+\frac{\mu}{\mathrm{1}+\mu}\right)−\mathrm{2}\mu\right]\left(\mathrm{1}−\frac{\mu}{\mathrm{1}+\mu}\right){lg}={v}^{\mathrm{2}} \\ $$$$\frac{{lg}}{\mathrm{1}+\mu}={v}^{\mathrm{2}} \\ $$$$\Rightarrow{v}=\sqrt{\frac{{lg}}{\mathrm{1}+\mu}} \\ $$
Commented by MrW3 last updated on 24/Jul/18
Thanks for checking!
$${Thanks}\:{for}\:{checking}! \\ $$
Commented by ajfour last updated on 24/Jul/18
I apologise Sir; its indeed correct. Thanks!
$${I}\:{apologise}\:{Sir};\:{its}\:{indeed}\:{correct}. \\ $$$${Thanks}! \\ $$
Commented by MrW3 last updated on 24/Jul/18
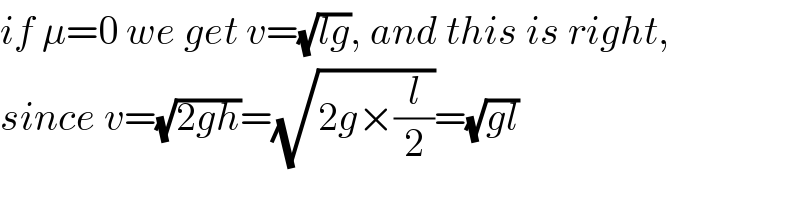
if μ=0 we get v=(√(lg)), and this is right, since v=(√(2gh))=(√(2g×(l/2)))=(√(gl))
$${if}\:\mu=\mathrm{0}\:{we}\:{get}\:{v}=\sqrt{{lg}},\:{and}\:{this}\:{is}\:{right}, \\ $$$${since}\:{v}=\sqrt{\mathrm{2}{gh}}=\sqrt{\mathrm{2}{g}×\frac{{l}}{\mathrm{2}}}=\sqrt{{gl}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *