Question Number 40615 by behi83417@gmail.com last updated on 24/Jul/18
Commented by behi83417@gmail.com last updated on 24/Jul/18
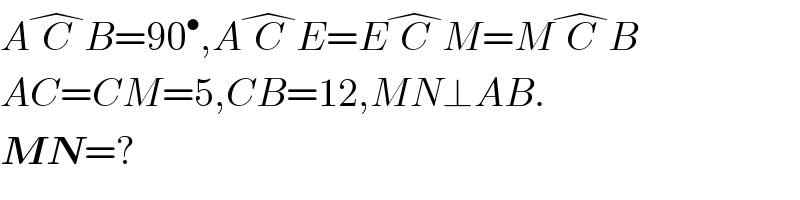
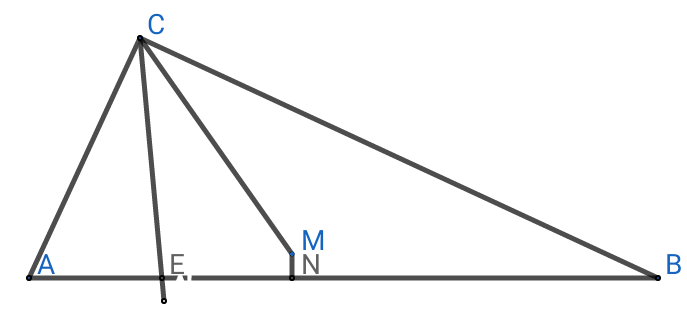
$${A}\overset{�} {{C}B}=\mathrm{90}^{\bullet} ,{A}\overset{�} {{C}E}={E}\overset{�} {{C}M}={M}\overset{�} {{C}B} \\ $$$${AC}={CM}=\mathrm{5},{CB}=\mathrm{12},{MN}\bot{AB}. \\ $$$$\boldsymbol{{MN}}=? \\ $$
Commented by ajfour last updated on 25/Jul/18
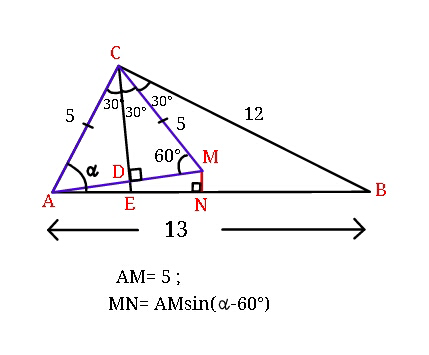
Answered by MJS last updated on 25/Jul/18
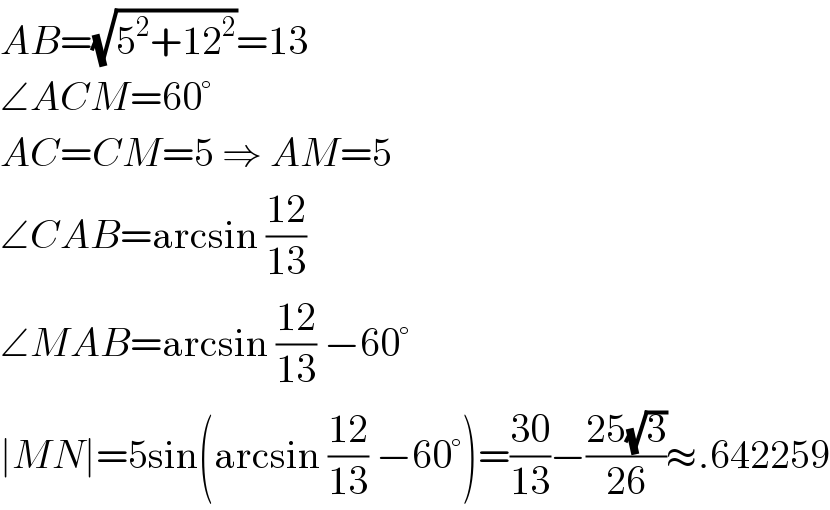
$${AB}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13} \\ $$$$\angle{ACM}=\mathrm{60}° \\ $$$${AC}={CM}=\mathrm{5}\:\Rightarrow\:{AM}=\mathrm{5} \\ $$$$\angle{CAB}=\mathrm{arcsin}\:\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\angle{MAB}=\mathrm{arcsin}\:\frac{\mathrm{12}}{\mathrm{13}}\:−\mathrm{60}° \\ $$$$\mid{MN}\mid=\mathrm{5sin}\left(\mathrm{arcsin}\:\frac{\mathrm{12}}{\mathrm{13}}\:−\mathrm{60}°\right)=\frac{\mathrm{30}}{\mathrm{13}}−\frac{\mathrm{25}\sqrt{\mathrm{3}}}{\mathrm{26}}\approx.\mathrm{642259} \\ $$
