Question-40625

Question Number 40625 by Raj Singh last updated on 25/Jul/18

Answered by MJS last updated on 25/Jul/18

∫(dx/( (√x)+(x)^(1/3) ))= [t=(x)^(1/6) → dx=6(x^5 )^(1/6) dt] =6∫(t^3 /(t+1))dt=6∫(t^2 −t+1−(1/(t+1)))dt= =6((1/3)t^3 −(1/2)t^2 +t−ln (t+1))= =2t^3 −3t^2 +6t−6ln (t+1)= =2(√x)−3(x)^(1/3) +6(x)^(1/6) −6ln (1+(x)^(1/6) ) +C

$$\int\frac{{dx}}{\:\sqrt{{x}}+\sqrt[{\mathrm{3}}]{{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{6}}]{{x}}\:\rightarrow\:{dx}=\mathrm{6}\sqrt[{\mathrm{6}}]{{x}^{\mathrm{5}} }{dt}\right] \\ $$$$=\mathrm{6}\int\frac{{t}^{\mathrm{3}} }{{t}+\mathrm{1}}{dt}=\mathrm{6}\int\left({t}^{\mathrm{2}} −{t}+\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$=\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{3}}{t}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +{t}−\mathrm{ln}\:\left({t}+\mathrm{1}\right)\right)= \\ $$$$=\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{6ln}\:\left({t}+\mathrm{1}\right)= \\ $$$$=\mathrm{2}\sqrt{{x}}−\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}+\mathrm{6}\sqrt[{\mathrm{6}}]{{x}}−\mathrm{6ln}\:\left(\mathrm{1}+\sqrt[{\mathrm{6}}]{{x}}\right)\:+{C} \\ $$

Commented by MJS last updated on 25/Jul/18

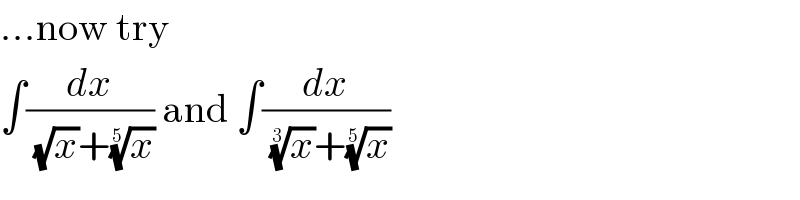
...now try ∫(dx/( (√x)+(x)^(1/5) )) and ∫(dx/( (x)^(1/3) +(x)^(1/5) ))

$$…\mathrm{now}\:\mathrm{try} \\ $$$$\int\frac{{dx}}{\:\sqrt{{x}}+\sqrt[{\mathrm{5}}]{{x}}}\:\mathrm{and}\:\int\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{5}}]{{x}}} \\ $$

Answered by Joel578 last updated on 25/Jul/18

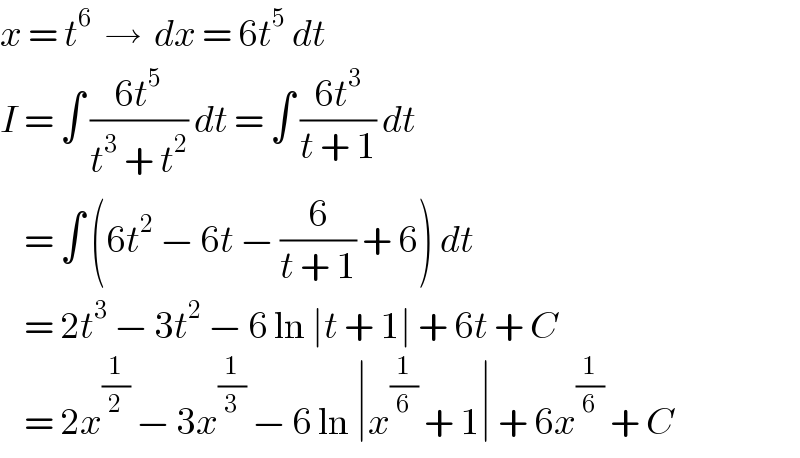
x = t^6 → dx = 6t^5 dt I = ∫ ((6t^5 )/(t^3 + t^2 )) dt = ∫ ((6t^3 )/(t + 1)) dt = ∫ (6t^2 − 6t − (6/(t + 1)) + 6) dt = 2t^3 − 3t^2 − 6 ln ∣t + 1∣ + 6t + C = 2x^(1/2) − 3x^(1/3) − 6 ln ∣x^(1/6) + 1∣ + 6x^(1/6) + C

$${x}\:=\:{t}^{\mathrm{6}} \:\:\rightarrow\:\:{dx}\:=\:\mathrm{6}{t}^{\mathrm{5}} \:{dt} \\ $$$${I}\:=\:\int\:\frac{\mathrm{6}{t}^{\mathrm{5}} }{{t}^{\mathrm{3}} \:+\:{t}^{\mathrm{2}} }\:{dt}\:=\:\int\:\frac{\mathrm{6}{t}^{\mathrm{3}} }{{t}\:+\:\mathrm{1}}\:{dt} \\ $$$$\:\:\:\:=\:\int\:\left(\mathrm{6}{t}^{\mathrm{2}} \:−\:\mathrm{6}{t}\:−\:\frac{\mathrm{6}}{{t}\:+\:\mathrm{1}}\:+\:\mathrm{6}\right)\:{dt} \\ $$$$\:\:\:\:=\:\mathrm{2}{t}^{\mathrm{3}} \:−\:\mathrm{3}{t}^{\mathrm{2}} \:−\:\mathrm{6}\:\mathrm{ln}\:\mid{t}\:+\:\mathrm{1}\mid\:+\:\mathrm{6}{t}\:+\:{C} \\ $$$$\:\:\:\:=\:\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \:−\:\mathrm{3}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \:−\:\mathrm{6}\:\mathrm{ln}\:\mid{x}^{\frac{\mathrm{1}}{\mathrm{6}}} \:+\:\mathrm{1}\mid\:+\:\mathrm{6}{x}^{\frac{\mathrm{1}}{\mathrm{6}}} \:+\:{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply