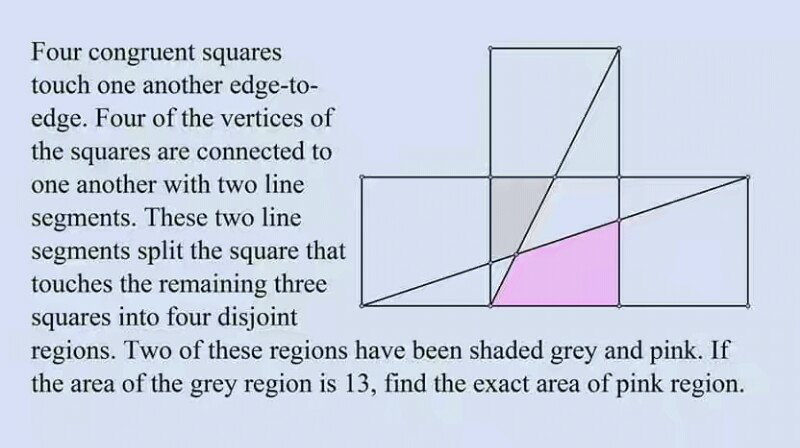
Question Number 40637 by Tawa1 last updated on 25/Jul/18
Answered by MJS last updated on 25/Jul/18
![l_1 : y=(x/3)+(a/3) l_2 : y=2x l_3 : y=a l_1 ∩l_2 (x/3)+(a/3)=2x ⇒ x=(a/5); y=((2a)/5) pink area ∫_0 ^(a/5) l_2 dx+∫_(a/5) ^a l_1 dx=[x^2 ]_0 ^(a/5) +[(x^2 /6)+((ax)/3)]_(a/5) ^a =((7a^2 )/(15)) grey area ∫_0 ^(a/5) (l_3 −l_1 )dx+∫_(a/5) ^(a/2) (l_3 −l_2 )dx=[((2ax)/3)−(x^2 /6)]_0 ^(a/5) +[ax−x^2 ]_(a/5) ^(a/2) =((13a^2 )/(60)) ((13a^2 )/(60))=13 ⇒ a=2(√(15)) ⇒ ((7a^2 )/(15))=28](https://www.tinkutara.com/question/Q40646.png)
$${l}_{\mathrm{1}} :\:{y}=\frac{{x}}{\mathrm{3}}+\frac{{a}}{\mathrm{3}} \\ $$$${l}_{\mathrm{2}} :\:{y}=\mathrm{2}{x} \\ $$$${l}_{\mathrm{3}} :\:{y}={a} \\ $$$${l}_{\mathrm{1}} \cap{l}_{\mathrm{2}} \\ $$$$\frac{{x}}{\mathrm{3}}+\frac{{a}}{\mathrm{3}}=\mathrm{2}{x}\:\Rightarrow\:{x}=\frac{{a}}{\mathrm{5}};\:{y}=\frac{\mathrm{2}{a}}{\mathrm{5}} \\ $$$$\mathrm{pink}\:\mathrm{area} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{{a}}{\mathrm{5}}} {\int}}{l}_{\mathrm{2}} {dx}+\underset{\frac{{a}}{\mathrm{5}}} {\overset{{a}} {\int}}{l}_{\mathrm{1}} {dx}=\left[{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{{a}}{\mathrm{5}}} +\left[\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{{ax}}{\mathrm{3}}\right]_{\frac{{a}}{\mathrm{5}}} ^{{a}} =\frac{\mathrm{7}{a}^{\mathrm{2}} }{\mathrm{15}} \\ $$$$\mathrm{grey}\:\mathrm{area} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{{a}}{\mathrm{5}}} {\int}}\left({l}_{\mathrm{3}} −{l}_{\mathrm{1}} \right){dx}+\underset{\frac{{a}}{\mathrm{5}}} {\overset{\frac{{a}}{\mathrm{2}}} {\int}}\left({l}_{\mathrm{3}} −{l}_{\mathrm{2}} \right){dx}=\left[\frac{\mathrm{2}{ax}}{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\right]_{\mathrm{0}} ^{\frac{{a}}{\mathrm{5}}} +\left[{ax}−{x}^{\mathrm{2}} \right]_{\frac{{a}}{\mathrm{5}}} ^{\frac{{a}}{\mathrm{2}}} =\frac{\mathrm{13}{a}^{\mathrm{2}} }{\mathrm{60}} \\ $$$$\frac{\mathrm{13}{a}^{\mathrm{2}} }{\mathrm{60}}=\mathrm{13}\:\Rightarrow\:{a}=\mathrm{2}\sqrt{\mathrm{15}}\:\Rightarrow\:\frac{\mathrm{7}{a}^{\mathrm{2}} }{\mathrm{15}}=\mathrm{28} \\ $$
Commented by Tawa1 last updated on 25/Jul/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by MrW3 last updated on 26/Jul/18
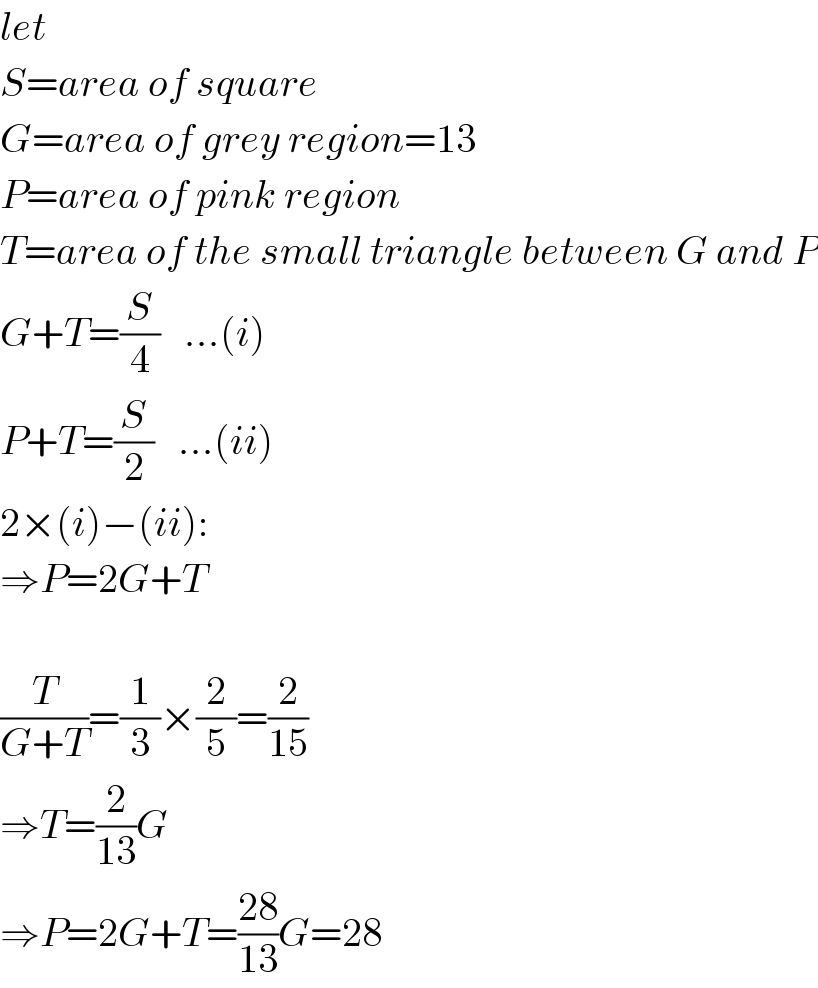
$${let} \\ $$$${S}={area}\:{of}\:{square} \\ $$$${G}={area}\:{of}\:{grey}\:{region}=\mathrm{13} \\ $$$${P}={area}\:{of}\:{pink}\:{region} \\ $$$${T}={area}\:{of}\:{the}\:{small}\:{triangle}\:{between}\:{G}\:{and}\:{P} \\ $$$${G}+{T}=\frac{{S}}{\mathrm{4}}\:\:\:…\left({i}\right) \\ $$$${P}+{T}=\frac{{S}}{\mathrm{2}}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{2}×\left({i}\right)−\left({ii}\right): \\ $$$$\Rightarrow{P}=\mathrm{2}{G}+{T} \\ $$$$ \\ $$$$\frac{{T}}{{G}+{T}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{2}}{\mathrm{15}} \\ $$$$\Rightarrow{T}=\frac{\mathrm{2}}{\mathrm{13}}{G} \\ $$$$\Rightarrow{P}=\mathrm{2}{G}+{T}=\frac{\mathrm{28}}{\mathrm{13}}{G}=\mathrm{28} \\ $$
