Menu Close

Question-40662

Tinku Tara 0 Comments
Pin




Question Number 40662 by Tinkutara last updated on 25/Jul/18
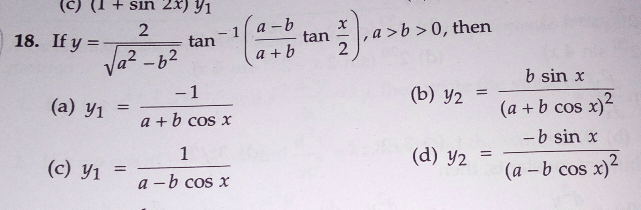
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18
pls check the question...it seems wrong...
$${pls}\:{check}\:{the}\:{question}…{it}\:{seems}\:{wrong}… \\ $$
Commented by maxmathsup by imad last updated on 25/Jul/18
if y_1 means derivative let w(x)=((√(a^2 −b^2 ))/2)y(x)⇒w(x)=arctan(((a−b)/(a+b))tan((x/2))) ⇒w^′ (x)=((((a−b)/(2(a+b))){1+tan^2 ((x/2))})/(1+(((a−b)^2 )/((a+b)^2 ))tan^2 ((x/2)))) =(((a−b))/(2(a+b)cos^2 ((x/2)){(((a+b)^2 +(a−b)^2 tan^2 ((x/2)))/((a+b)^2 ))})) =((a^2 −b^2 )/(2cos^2 ((x/2)){(a+b)^2 +(a−b)^2 ((1/(cos^2 ((x/2))))−1)})) =((a^2 −b^2 )/(2 cos^2 ((x/2)){(a+b)^2 cos^2 ((x/2)) +(a−b)^2 (1−cos^2 ((x/2)))(1/(cos^2 ((x/2)))))) = ((a^2 −b^2 )/(2{ ( (a+b)^2 −(a−b^2 ))cos^2 ((x/2)) +(a−b)^2 })) =((a^2 −b^2 )/(2{ 4ab cos^2 ((x/2)) +(a−b)^2 })) =((a^2 −b^2 )/(4ab(1+cosx) +2(a^2 −2ab +b^2 ))) =((a^2 −b^2 )/(4ab cosx +2a^2 +2b^2 )) = ((a^2 −b^2 )/(2(a^2 +b^2 +2ab cosx))) ⇒ y^((1)) (x) =(2/( (√(a^2 −b^2 ))))w^′ (x) = ((√(a^2 −b^2 ))/(a^2 +b^2 +2ab cosx)) so something went wrong in the question...
$${if}\:{y}_{\mathrm{1}} {means}\:{derivative}\:{let}\:{w}\left({x}\right)=\frac{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }}{\mathrm{2}}{y}\left({x}\right)\Rightarrow{w}\left({x}\right)={arctan}\left(\frac{{a}−{b}}{{a}+{b}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$\Rightarrow{w}^{'} \left({x}\right)=\frac{\frac{{a}−{b}}{\mathrm{2}\left({a}+{b}\right)}\left\{\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right\}}{\mathrm{1}+\frac{\left({a}−{b}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:=\frac{\left({a}−{b}\right)}{\mathrm{2}\left({a}+{b}\right){cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\left\{\frac{\left({a}+{b}\right)^{\mathrm{2}} \:+\left({a}−{b}\right)^{\mathrm{2}} {tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\left({a}+{b}\right)^{\mathrm{2}} }\right\}} \\ $$$$=\frac{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\left\{\left({a}+{b}\right)^{\mathrm{2}} \:+\left({a}−{b}\right)^{\mathrm{2}} \left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}−\mathrm{1}\right)\right\}} \\ $$$$=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}\:{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\left\{\left({a}+{b}\right)^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:+\left({a}−{b}\right)^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right.} \\ $$$$=\:\frac{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }{\mathrm{2}\left\{\:\:\left(\:\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}^{\mathrm{2}} \right)\right){cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:+\left({a}−{b}\right)^{\mathrm{2}} \right\}} \\ $$$$=\frac{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} }{\mathrm{2}\left\{\:\:\mathrm{4}{ab}\:{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:+\left({a}−{b}\right)^{\mathrm{2}} \right\}}\:=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{ab}\left(\mathrm{1}+{cosx}\right)\:+\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{2}{ab}\:+{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4}{ab}\:{cosx}\:+\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} }\:=\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\mathrm{2}{ab}\:{cosx}\right)}\:\Rightarrow \\ $$$${y}^{\left(\mathrm{1}\right)} \left({x}\right)\:=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}{w}^{'} \left({x}\right)\:=\:\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:+\mathrm{2}{ab}\:{cosx}}\:\:{so}\:{something}\:{went}\:{wrong}\:{in}\:{the} \\ $$$${question}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jul/18
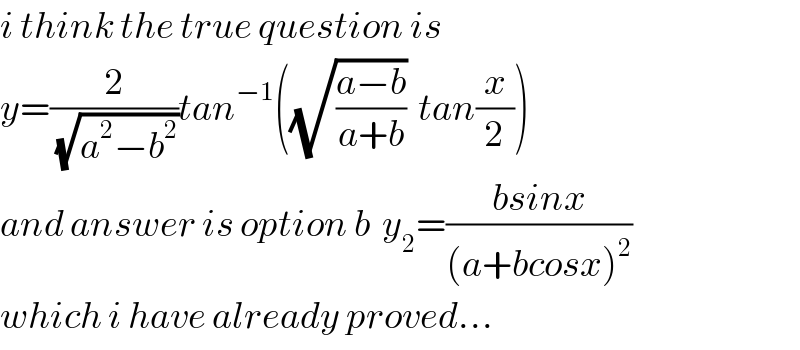
i think the true question is y=(2/( (√(a^2 −b^2 ))))tan^(−1) ((√((a−b)/(a+b))) tan(x/2)) and answer is option b y_2 =((bsinx)/((a+bcosx)^2 )) which i have already proved...
$${i}\:{think}\:{the}\:{true}\:{question}\:{is}\: \\ $$$${y}=\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{a}−{b}}{{a}+{b}}}\:\:{tan}\frac{{x}}{\mathrm{2}}\right) \\ $$$${and}\:{answer}\:{is}\:{option}\:{b}\:\:{y}_{\mathrm{2}} =\frac{{bsinx}}{\left({a}+{bcosx}\right)^{\mathrm{2}} } \\ $$$${which}\:{i}\:{have}\:{already}\:{proved}… \\ $$
Commented by Tinkutara last updated on 27/Jul/18
Thanks Sir imad.
Commented by math khazana by abdo last updated on 28/Jul/18
you are welcome sir.
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jul/18
Commented by Tinkutara last updated on 25/Jul/18
Sir no option matching?
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jul/18
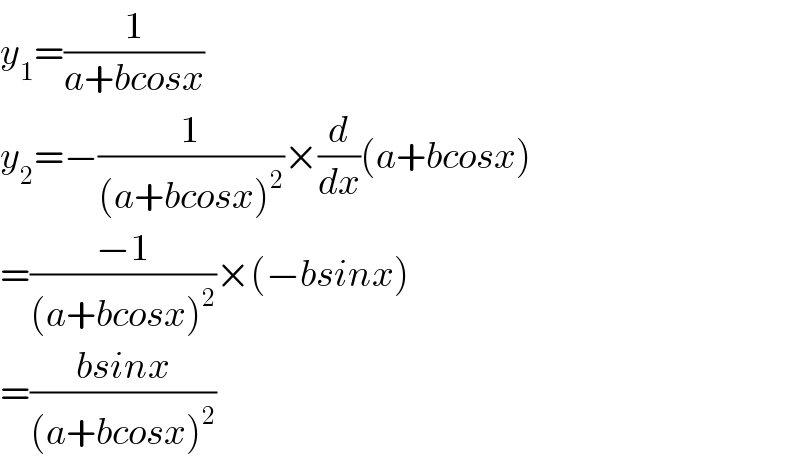
y_1 =(1/(a+bcosx)) y_2 =−(1/((a+bcosx)^2 ))×(d/dx)(a+bcosx) =((−1)/((a+bcosx)^2 ))×(−bsinx) =((bsinx)/((a+bcosx)^2 ))
$${y}_{\mathrm{1}} =\frac{\mathrm{1}}{{a}+{bcosx}} \\ $$$${y}_{\mathrm{2}} =−\frac{\mathrm{1}}{\left({a}+{bcosx}\right)^{\mathrm{2}} }×\frac{{d}}{{dx}}\left({a}+{bcosx}\right) \\ $$$$=\frac{−\mathrm{1}}{\left({a}+{bcosx}\right)^{\mathrm{2}} }×\left(−{bsinx}\right)\: \\ $$$$=\frac{{bsinx}}{\left({a}+{bcosx}\right)^{\mathrm{2}} } \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/Jul/18
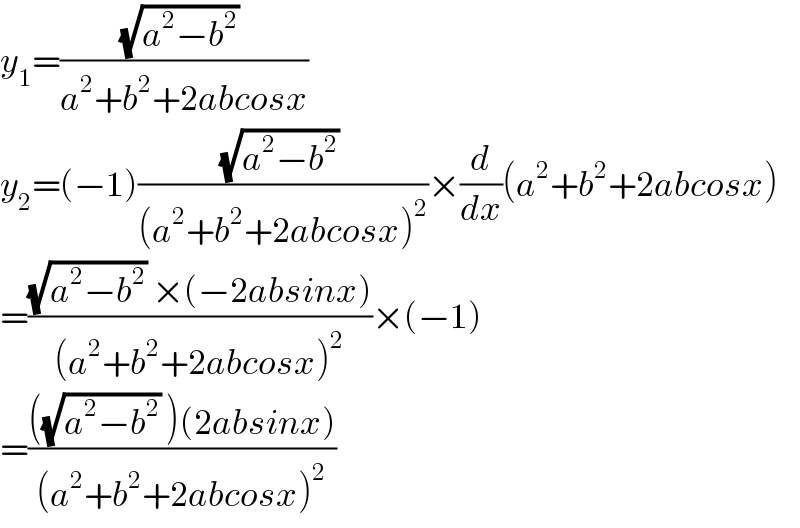
y_1 =(((√(a^2 −b^2 )) )/(a^2 +b^2 +2abcosx)) y_2 =(−1)(((√(a^2 −b^2 )) )/((a^2 +b^2 +2abcosx)^2 ))×(d/dx)(a^2 +b^2 +2abcosx) =(((√(a^2 −b^2 )) ×(−2absinx))/((a^2 +b^2 +2abcosx)^2 ))×(−1) =((((√(a^2 −b^2 )) )(2absinx))/((a^2 +b^2 +2abcosx)^2 ))
$${y}_{\mathrm{1}} =\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{abcosx}} \\ $$$${y}_{\mathrm{2}} =\left(−\mathrm{1}\right)\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{abcosx}\right)^{\mathrm{2}} }×\frac{{d}}{{dx}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{abcosx}\right) \\ $$$$=\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:×\left(−\mathrm{2}{absinx}\right)}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{abcosx}\right)^{\mathrm{2}} }×\left(−\mathrm{1}\right) \\ $$$$=\frac{\left(\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\right)\left(\mathrm{2}{absinx}\right)}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{abcosx}\right)^{\mathrm{2}} } \\ $$
Commented by Tinkutara last updated on 27/Jul/18
Thank you very much Sir! I got the answer. ��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *