Question Number 40740 by goal last updated on 27/Jul/18

Commented by goal last updated on 27/Jul/18

$${thank}\:{you}\:{sir} \\ $$
Commented by goal last updated on 27/Jul/18
$${question}\:{no}.\:\mathrm{9}\:{please}\:{solve}\:{this} \\ $$
Commented by goal last updated on 27/Jul/18
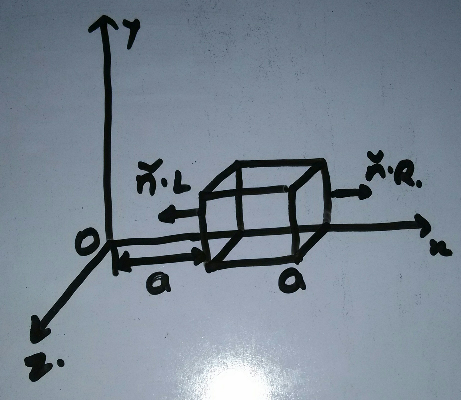
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18

$${flux}\:{for}\:{left}\:{plane}\:{at}\:{a}\:{distance}\:{a}\:{from}\:{origin} \\ $$$$\psi_{\mathrm{1}} =\alpha{a}^{\frac{\mathrm{1}}{\mathrm{2}}} {a}^{\mathrm{2}} {cos}\mathrm{180}^{\mathrm{0}} \\ $$$$\:\:=−\alpha{a}^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$$\psi_{\mathrm{2}} =\alpha\left(\mathrm{2}{a}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {a}^{\mathrm{2}} {cos}\mathrm{0}^{{o}} \:\:{for}\:{right}\:{plane} \\ $$$$\:\:=\alpha.\sqrt{\mathrm{2}}\:.{a}^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$${totalflux}=\alpha{a}^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right) \\ $$$$\oint{E}.{ds}=\frac{{Q}}{\epsilon_{\mathrm{0}} }\:\: \\ $$$${charge}=\frac{\alpha{a}^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)×\epsilon_{\mathrm{0}} }{} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18

$${its}\:{ok}… \\ $$
