Menu Close

Question-40745

Tinku Tara 0 Comments
Pin




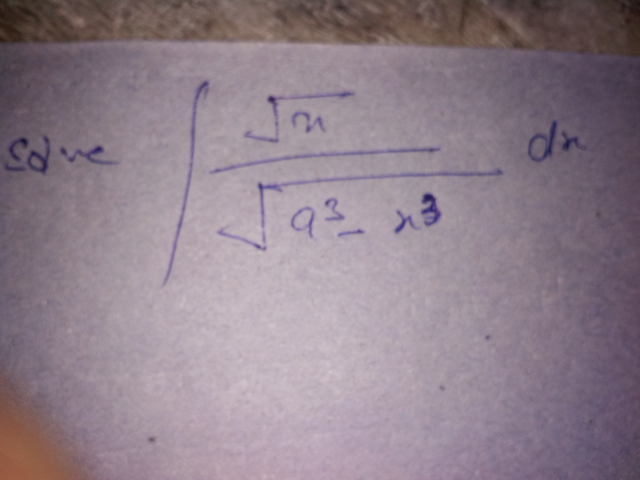
Question Number 40745 by Raj Singh last updated on 27/Jul/18
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18
x^3 =a^3 sin^2 α 3x^2 dx=a^3 .2sinαcosα dα dx=((2a^3 sinαcosα)/(3(a^3 sin^2 α)^(2/3) ))=(2/3)a.sin^((−1)/3) αcosα dα ∫(((a^3 sin^2 α)^(1/6) ×(2/3)asin^((−1)/3) αcosα dα)/((a^3 −a^3 sin^2 α)^(1/2) )) (2/3)∫(a^((3/6)+1−(3/2)) /)×sin^((2/6)−(1/(3 ))) α dα (2/3)α +c sinα=((x/a))^(3/2) α=sin^(−1) {((x/a))^(3/2) } ans is (2/3)sin^(−1) {((x/a))^(3/2) } +c check y=(2/3)sin^(−1) {((x/a))^(3/2) }+c (dy/dx)=(2/3)×(1/( (√(1−((x/a))^3 )))) ×(3/2)×((x/a))^(1/2) ×(1/a) =a^((3/2)−1−(1/2) ) .(((√x) )/( (√(a^3 −x^3 )))) =(((√x) )/( (√(a^3 −x^3 ))))
$${x}^{\mathrm{3}} ={a}^{\mathrm{3}} {sin}^{\mathrm{2}} \alpha \\ $$$$\mathrm{3}{x}^{\mathrm{2}} {dx}={a}^{\mathrm{3}} .\mathrm{2}{sin}\alpha{cos}\alpha\:{d}\alpha \\ $$$${dx}=\frac{\mathrm{2}{a}^{\mathrm{3}} {sin}\alpha{cos}\alpha}{\mathrm{3}\left({a}^{\mathrm{3}} {sin}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }=\frac{\mathrm{2}}{\mathrm{3}}{a}.{sin}^{\frac{−\mathrm{1}}{\mathrm{3}}} \alpha{cos}\alpha\:{d}\alpha \\ $$$$\int\frac{\left({a}^{\mathrm{3}} {sin}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{1}}{\mathrm{6}}} ×\frac{\mathrm{2}}{\mathrm{3}}{asin}^{\frac{−\mathrm{1}}{\mathrm{3}}} \alpha{cos}\alpha\:{d}\alpha}{\left({a}^{\mathrm{3}} −{a}^{\mathrm{3}} {sin}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{a}^{\frac{\mathrm{3}}{\mathrm{6}}+\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}} }{}×{sin}^{\frac{\mathrm{2}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{3}\:}} \alpha\:{d}\alpha \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\alpha\:+{c} \\ $$$${sin}\alpha=\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\:\alpha={sin}^{−\mathrm{1}} \left\{\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\} \\ $$$${ans}\:{is}\:\frac{\mathrm{2}}{\mathrm{3}}{sin}^{−\mathrm{1}} \left\{\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}\:+{c} \\ $$$${check} \\ $$$${y}=\frac{\mathrm{2}}{\mathrm{3}}{sin}^{−\mathrm{1}} \left\{\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}+{c} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\frac{{x}}{{a}}\right)^{\mathrm{3}} }}\:×\frac{\mathrm{3}}{\mathrm{2}}×\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\frac{\mathrm{1}}{{a}} \\ $$$$={a}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:} .\frac{\sqrt{{x}}\:}{\:\sqrt{{a}^{\mathrm{3}} −{x}^{\mathrm{3}} }}\:\:=\frac{\sqrt{{x}}\:}{\:\sqrt{{a}^{\mathrm{3}} −{x}^{\mathrm{3}} }}\: \\ $$$$ \\ $$
Answered by MJS last updated on 27/Jul/18
a≠0 ∫((√x)/( (√(a^3 −x^3 ))))dx= [t=(x^(3/2) /a^(3/2) ) 3→ dx=((2a^(3/2) )/(3(√x)))dt] =(2/3)∫(1/( (√(1−t^2 ))))=(2/3)arcsin t =(2/3)arcsin ((x/a))^(3/2) +C a=0 ∫((√x)/( (√(−x^3 ))))dx=∫(√(−(1/x^2 )))dx=i∫(dx/(∣x∣))=i×sign(x)ln∣x∣+C
$${a}\neq\mathrm{0} \\ $$$$\int\frac{\sqrt{{x}}}{\:\sqrt{{a}^{\mathrm{3}} −{x}^{\mathrm{3}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{{a}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\mathrm{3}\rightarrow\:{dx}=\frac{\mathrm{2}{a}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}\sqrt{{x}}}{dt}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:{t}\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$$$ \\ $$$${a}=\mathrm{0} \\ $$$$\int\frac{\sqrt{{x}}}{\:\sqrt{−{x}^{\mathrm{3}} }}{dx}=\int\sqrt{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}=\mathrm{i}\int\frac{{dx}}{\mid{x}\mid}=\mathrm{i}×\mathrm{sign}\left({x}\right)\mathrm{ln}\mid{x}\mid+{C} \\ $$
Answered by math khazana by abdo last updated on 27/Jul/18
let I = ∫ ((√x)/( (√(a^3 −x^3 ))))dx changement x=at give I = ∫ (((√a)(√t))/( (√a^3 )(√(1−t^3 )))) adt = ∫ ((√t)/( (√(1−t^3 )))) dt =_(t^3 =sin^2 α) ∫ ((√(sinα^(2/3) ))/(cosα)) (2/3)cosα sinα^((2/3)−1) dα (t=sinα^(2/3) ) = (2/3)∫ (((sinα)^(1/3) (sinα)^(−(1/3)) )/(cosα)) cosα dα =(2/3)∫ dα = (2/3) α +c = (2/3) arcsin(t^(3/2) ) +c =(2/3) arcsin( ((x/a))^(3/2) ) +c ⇒ I = (2/3) arcsin((√(x^3 /a^3 ))) +c (we suppose a>0)
$${let}\:{I}\:=\:\int\:\:\:\:\frac{\sqrt{{x}}}{\:\sqrt{{a}^{\mathrm{3}} −{x}^{\mathrm{3}} }}{dx}\:{changement}\:{x}={at}\:{give} \\ $$$${I}\:=\:\int\:\:\:\frac{\sqrt{{a}}\sqrt{{t}}}{\:\sqrt{{a}^{\mathrm{3}} }\sqrt{\mathrm{1}−{t}^{\mathrm{3}} }}\:{adt}\:=\:\int\:\:\:\frac{\sqrt{{t}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{3}} }}\:{dt} \\ $$$$=_{{t}^{\mathrm{3}} ={sin}^{\mathrm{2}} \alpha} \:\:\:\:\:\int\:\:\:\:\:\:\:\frac{\sqrt{{sin}\alpha^{\frac{\mathrm{2}}{\mathrm{3}}} }}{{cos}\alpha}\:\frac{\mathrm{2}}{\mathrm{3}}{cos}\alpha\:{sin}\alpha^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} {d}\alpha\:\:\:\:\:\:\left({t}={sin}\alpha^{\frac{\mathrm{2}}{\mathrm{3}}} \right) \\ $$$$=\:\:\frac{\mathrm{2}}{\mathrm{3}}\int\:\:\:\:\:\:\frac{\left({sin}\alpha\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:\left({sin}\alpha\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} }{{cos}\alpha}\:{cos}\alpha\:{d}\alpha \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\:\:{d}\alpha\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\alpha\:+{c}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:{arcsin}\left({t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:{arcsin}\left(\:\left(\frac{{x}}{{a}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right)\:+{c}\:\:\Rightarrow \\ $$$${I}\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:{arcsin}\left(\sqrt{\frac{{x}^{\mathrm{3}} }{{a}^{\mathrm{3}} }}\right)\:+{c}\:\left({we}\:{suppose}\:{a}>\mathrm{0}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *